単変量解析と多変量解析: 違いは何ですか?

一変量分析という用語は、1 つの変数の分析を指します。接頭辞「uni」は「1」を意味するので、これを覚えておくとよいでしょう。

多変量解析という用語は、複数の変数の分析を指します。接頭語「multi」は「複数」を意味するため、これを覚えておくとよいでしょう。

一変量解析を実行するには、次の 3 つの一般的な方法があります。

1. 概要統計

• 変数の平均や中央値などの中心傾向の尺度を計算できます。
• 変数の標準偏差などの分散の尺度を計算することもできます。

2. 度数分布

• 変数の各値がどのくらいの頻度で現れるかを示す度数分布を作成できます。

3. グラフィックス

• 箱ひげ図、ヒストグラム、密度プロットなどのグラフを作成できます。変数の値の分布を視覚化します。

多変量解析を実行するには 2 つの一般的な方法があります。

1. 散布図行列

• 散布図行列を作成すると、データセット内の変数のペアごとの組み合わせ間の関係を視覚化できます。

2. 機械学習アルゴリズム

• 教師あり学習アルゴリズムを使用して、複数の予測変数と応答変数の間の関係を定量化する重線形回帰などのモデルを適合できます。
• 主成分分析のような教師なし学習アルゴリズムを使用して、データセット内の複数の変数間の構造と関係を同時に見つけることもできます。

次の例は、次のデータ セットを使用して単変量分析および多変量分析を実行する方法を示しています。

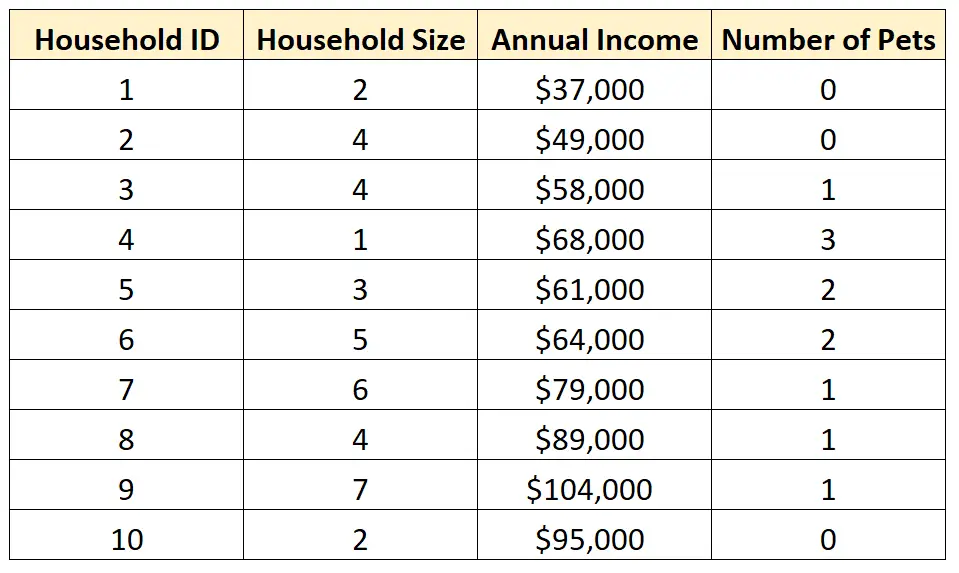
注: 正確に 2 つの変数を分析する場合、それは二変量分析と呼ばれます。

例: 単変量解析を実行する方法

データセット内の個々の変数のいずれかに対して単変量分析を実行することを選択できます。

たとえば、変数世帯規模に対して単変量分析を実行することを選択できます。

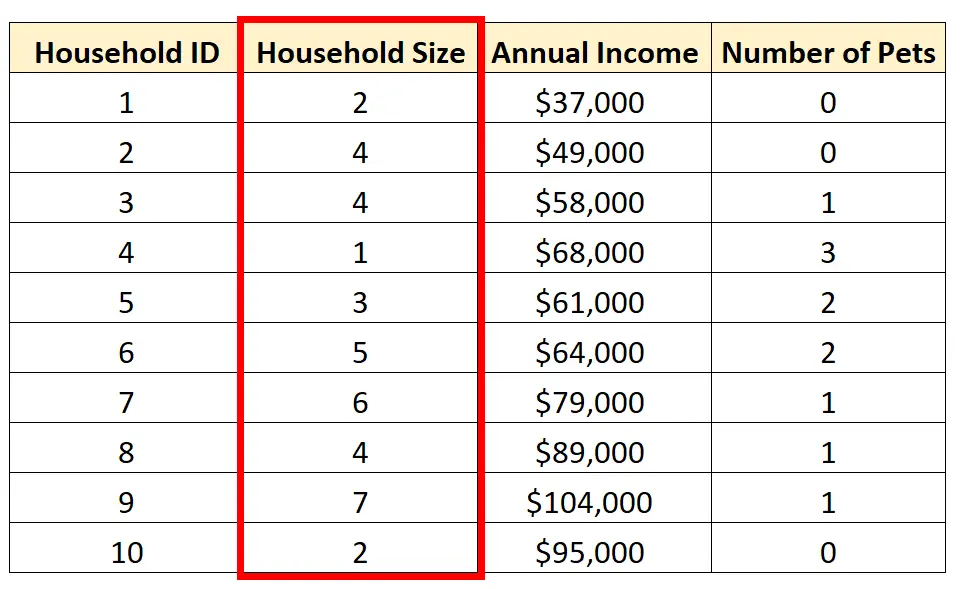
世帯人数の中心的な傾向を示す以下の尺度を計算できます。

• アベレージ（平均値）：3.8
• 中央値（平均値）：4

これらの価値観は、「中心的な」価値観がどこにあるかについてのアイデアを与えてくれます。

次の分散尺度を計算することもできます。

• 範囲 (最大値と最小値の差): 6
• 四分位スケール (値の中央 50% の分布): 2.5
• 標準偏差 (スプレッドの平均尺度): 1.87

これらの値は、この変数の値の分布のアイデアを与えてくれます。

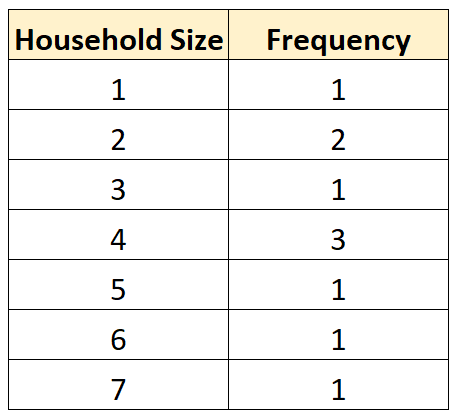
異なる値がどのくらいの頻度で発生するかを要約する次の度数分布表を作成することもできます。

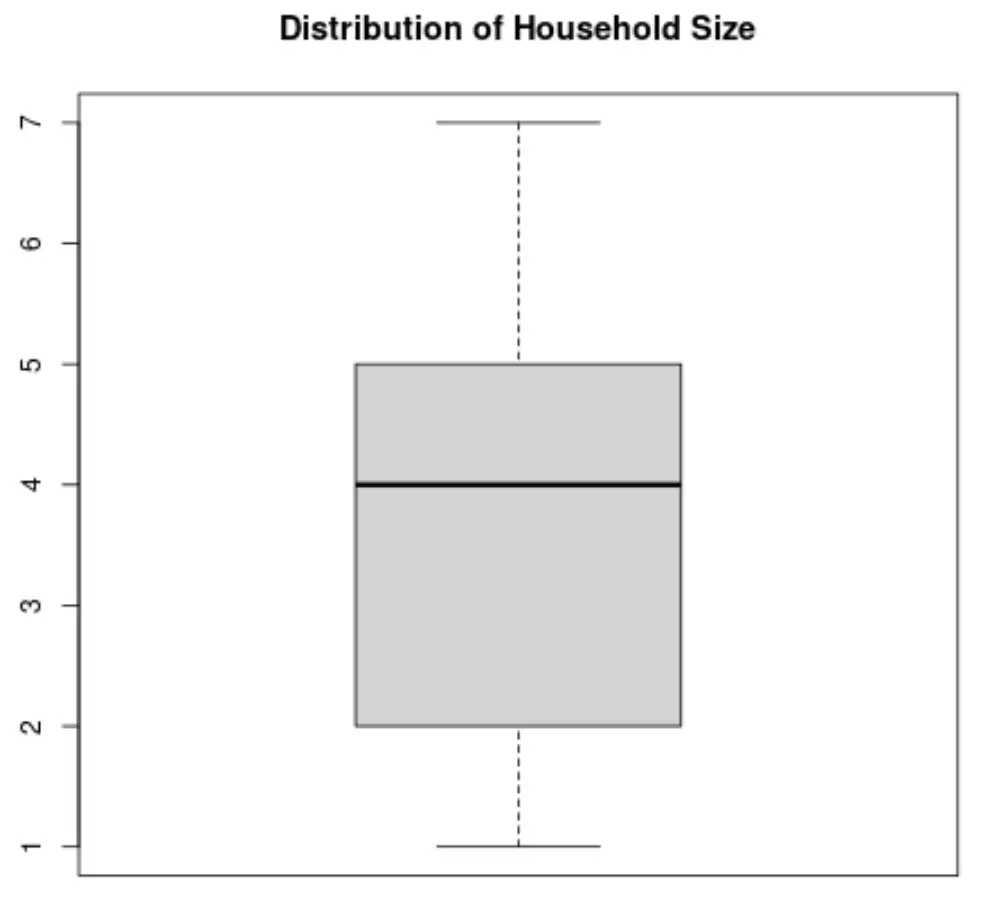
箱ひげ図を作成して、世帯人数に応じた値の分布を視覚化することもできます。

あるいは、ヒストグラムを作成して値の分布を視覚化することもできます。

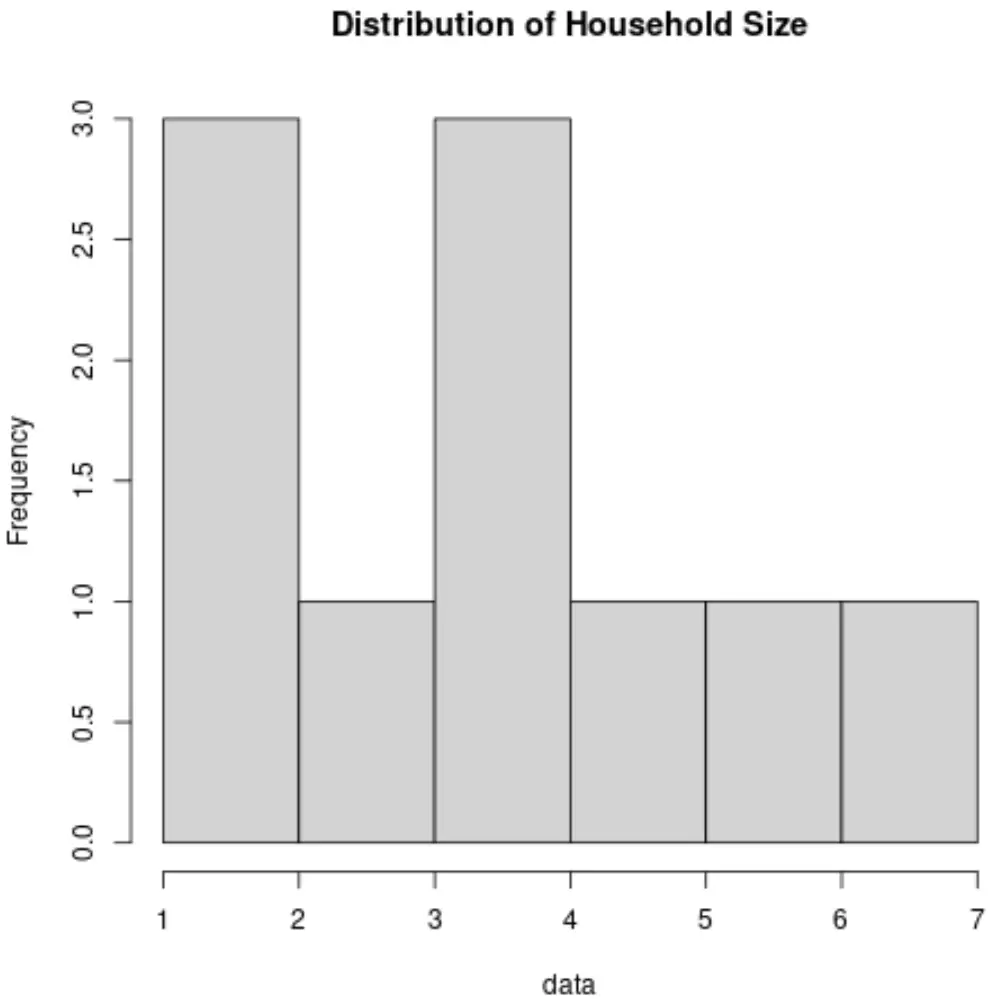
これらの測定値を計算してグラフを作成することで、世帯人数変数の値がどのように分布しているかをよりよく理解できます。

例: 多変量解析を実行する方法

もう一度、同じデータセットがあると仮定してみましょう。

このデータセットに対して実行できる多変量解析の簡単な形式は、散布図行列を作成することです。これは、データセット内の数値変数のペアごとの組み合わせごとに散布図を示す行列です。

このタイプのマトリックスを作成して、世帯人数、年収、ペットの数の関係を同時に視覚化できます。

リソース: R で散布図行列を作成する方法については、このチュートリアルを参照してください。

このデータセットに対して多変量解析を実行する別の方法は、重線形回帰モデルを当てはめることです。たとえば、世帯規模とペットの数を使用して年収を予測する回帰モデルを作成できます。

リソース: R で重線形回帰を実行する方法については、このチュートリアルを参照してください。

このデータセットに対して多変量解析を実行するもう 1 つの方法は、主成分分析を実行することです。これにより、データセット内の基礎となる構造を見つけることができます。

リソース: R で主成分分析を実行する方法については、このチュートリアルを参照してください。

結論

この記事の簡単な要約は次のとおりです。

• 単変量分析は 1 つの変数の分析です。
• 多変量分析は、複数の変数の分析です。
• 最終目標に応じて、各タイプの分析を実行するさまざまな方法があります。
• 現実の世界では、単一のデータセットに対して両方のタイプの分析を実行することがよくあります。
• 単変量解析では変数の値の分布を理解でき、多変量解析では複数の変数間の関係を理解できます。