単峰性分布とは何ですか? (定義&例)
単峰分布は、明確なピークを持つ確率分布です。
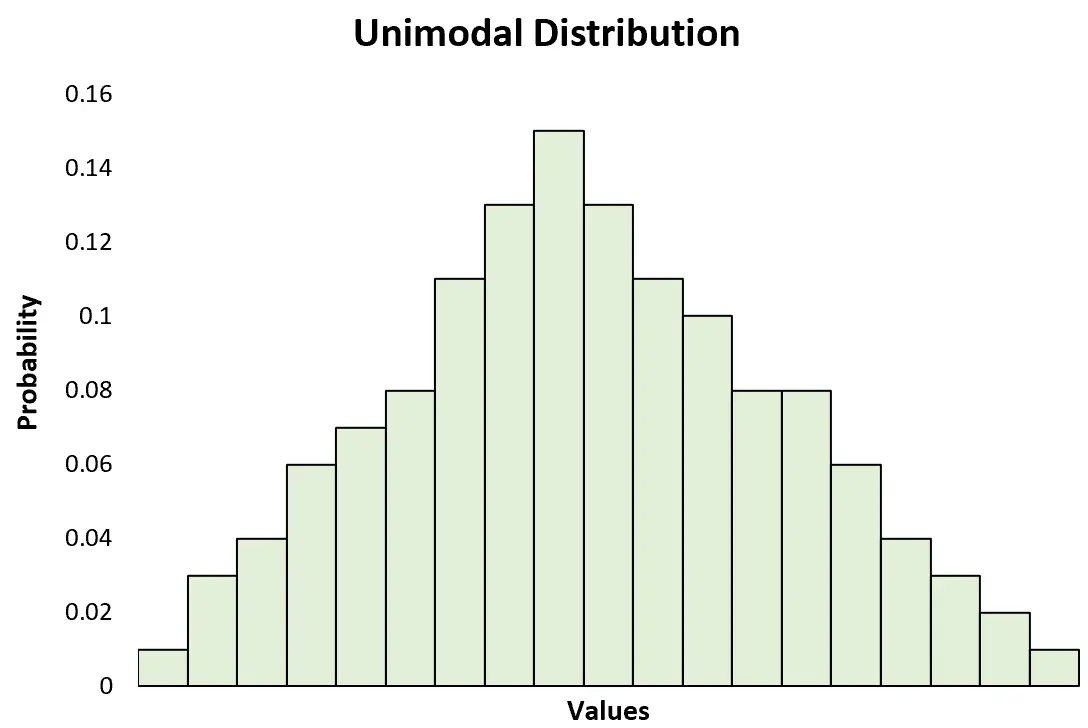
これは、2 つの明確なピークがある二峰性分布とは対照的です。
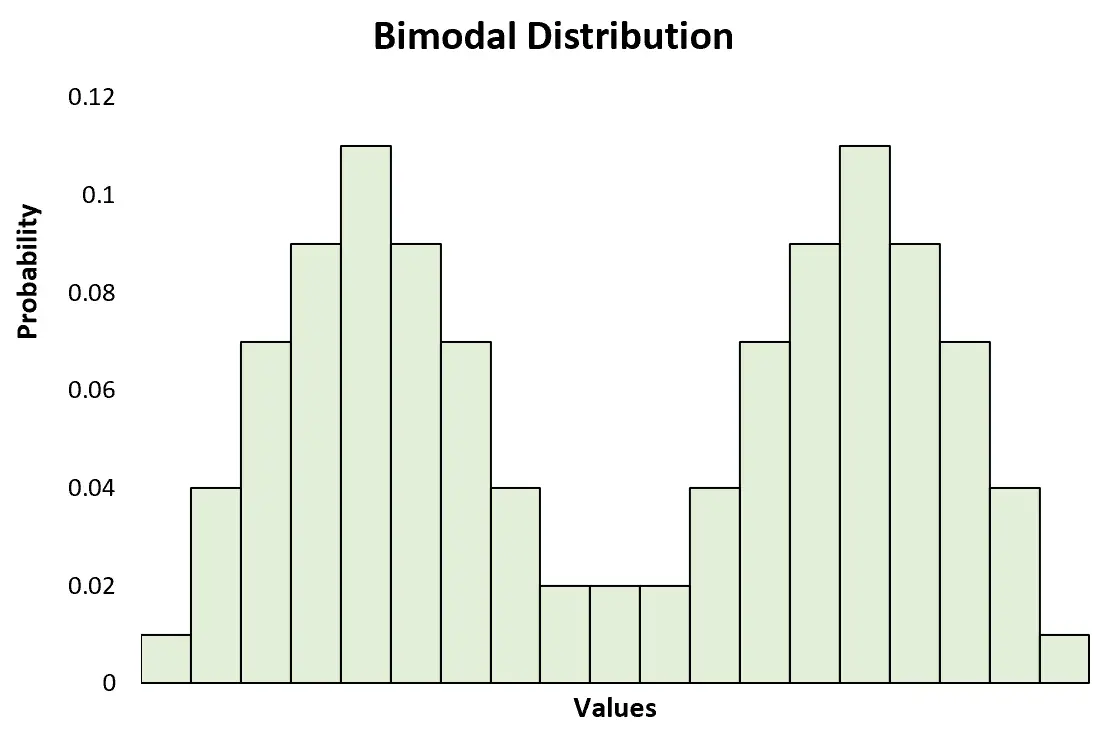
これは、2 つ以上のピークを持つ 多峰性分布とも対照的です。
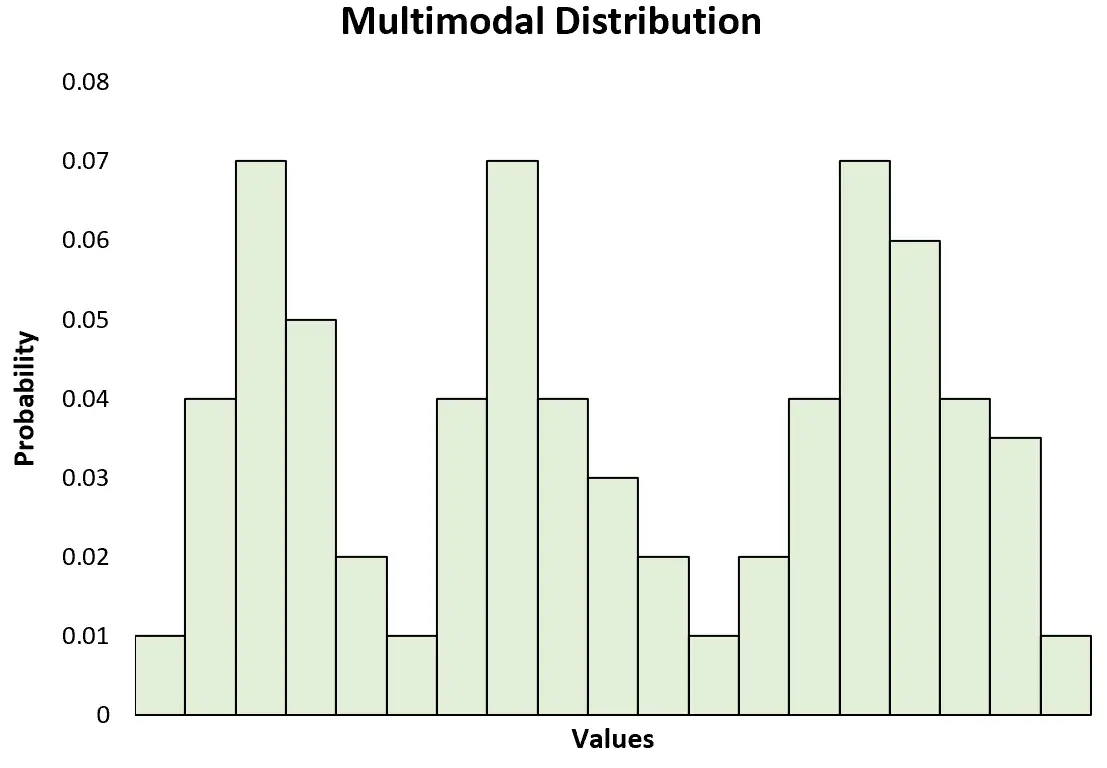
注:二峰性分布は、多峰性分布の特定のタイプにすぎません。
単峰性分布の例
実際の単峰分布の例をいくつか示します。
例 1: 赤ちゃんの出生体重
新生児の体重分布は単峰分布に従い、平均約 7.5 ポンドであることがよく知られています。赤ちゃんの体重のヒストグラムを作成すると、7.5 ポンドが「ピーク」で、それよりも体重が重い赤ちゃんもいれば、それより少ない赤ちゃんもいます。

例 2: ACT スコア
米国の高校生の平均 ACT スコアは約 21 ですが、これより低いスコアの生徒もいれば、より高いスコアの生徒もいます。米国の全生徒の ACT スコアのヒストグラムを作成すると、21 歳に単一の「ピーク」があり、一部の生徒のスコアが高く、他の生徒のスコアが低いことがわかります。
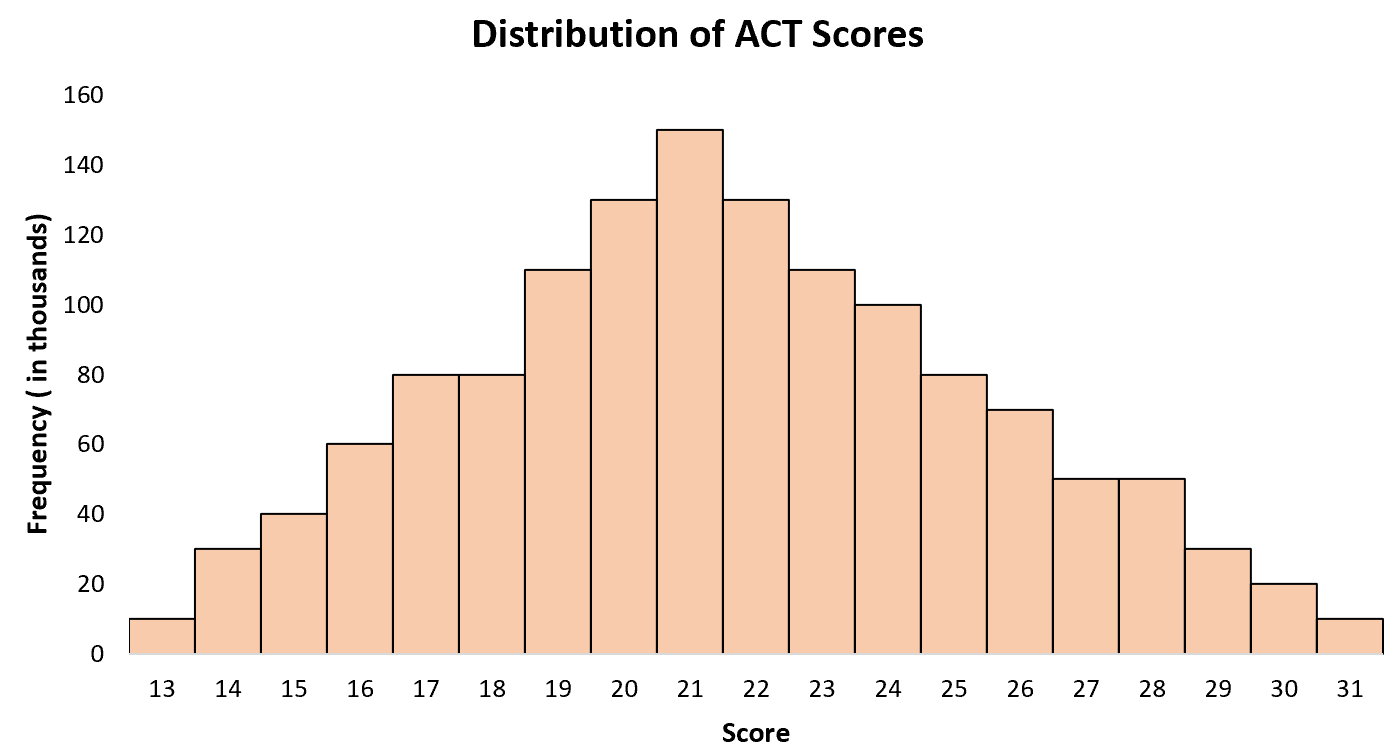
例 3: 靴のサイズ
男性の靴のサイズの分布は、10 付近に「ピーク」がある単峰分布です。すべての男性の靴のサイズのヒストグラムを作成すると、10 に単一のピークがあり、一部の男性はより大きな靴のサイズを履いており、他の男性はより大きな靴のサイズを履いていることがわかります。サイズ。より小さいサイズ。
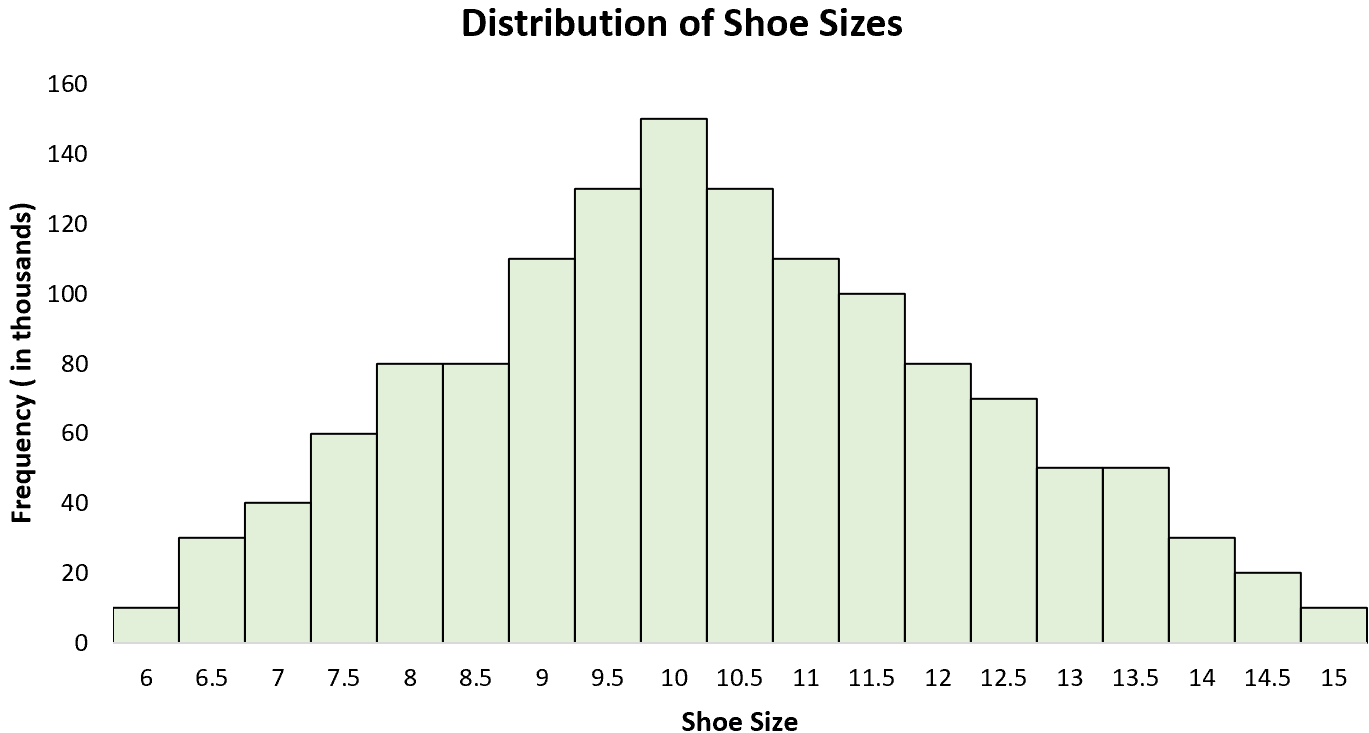
統計における単峰分布
統計における次の確率分布はすべて単峰分布です。
正規分布
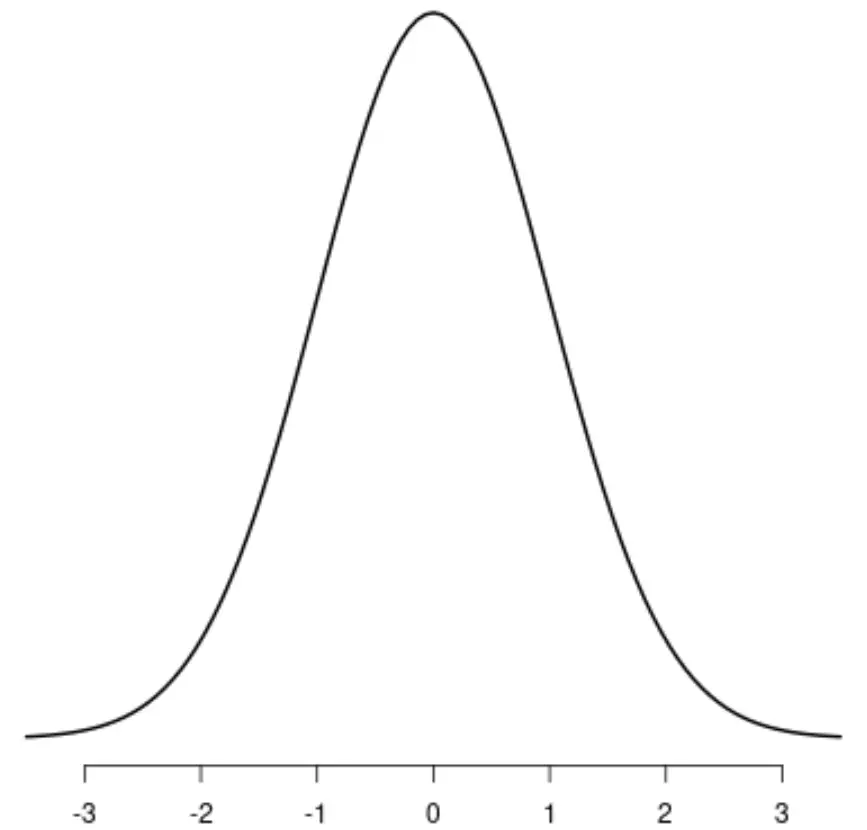
分布 t
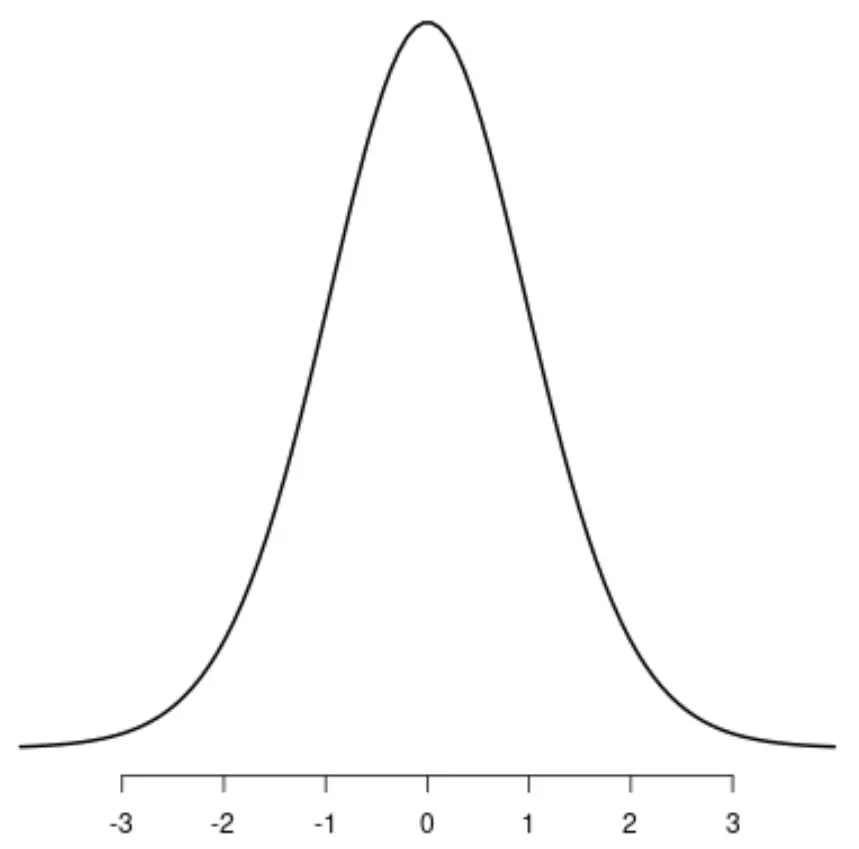
均一分布

コーシー分布
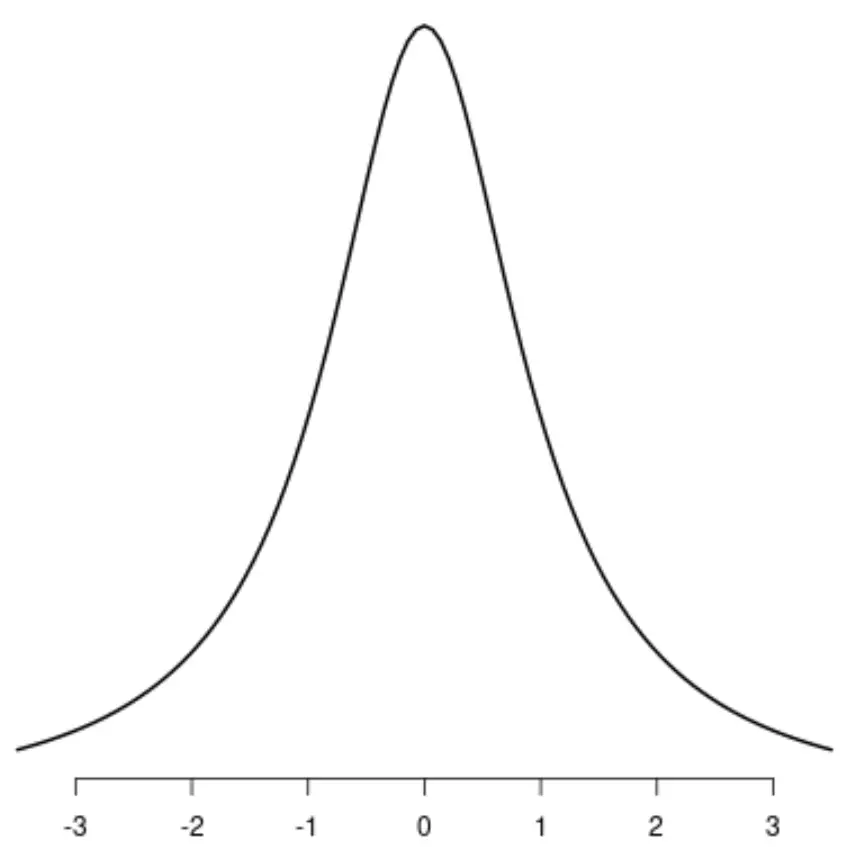
これらの分布にはそれぞれ 1 つの異なるピークがあることに注意してください。
単峰分布を分析する方法
私たちはよく、中心傾向の 3 つの異なる尺度を使用して単峰分布を説明します。
- 平均: 平均値
- Median : 中央値
- Mode : 最も頻繁に現れる値
分布の非対称性に応じて、これら 3 つの測定値は異なる場所で見つかる可能性があります。
左に歪んだ分布:平均値 < 中央値 < 最頻値
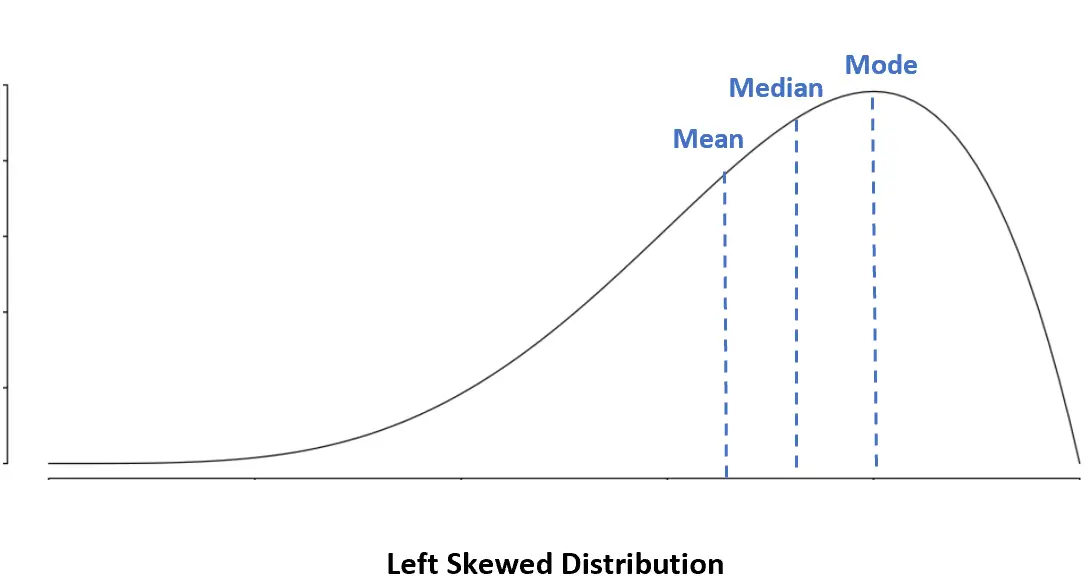
左に歪んだ分布では、平均値は中央値よりも小さくなります。
右に歪んだ分布:最頻値 < 中央値 < 平均
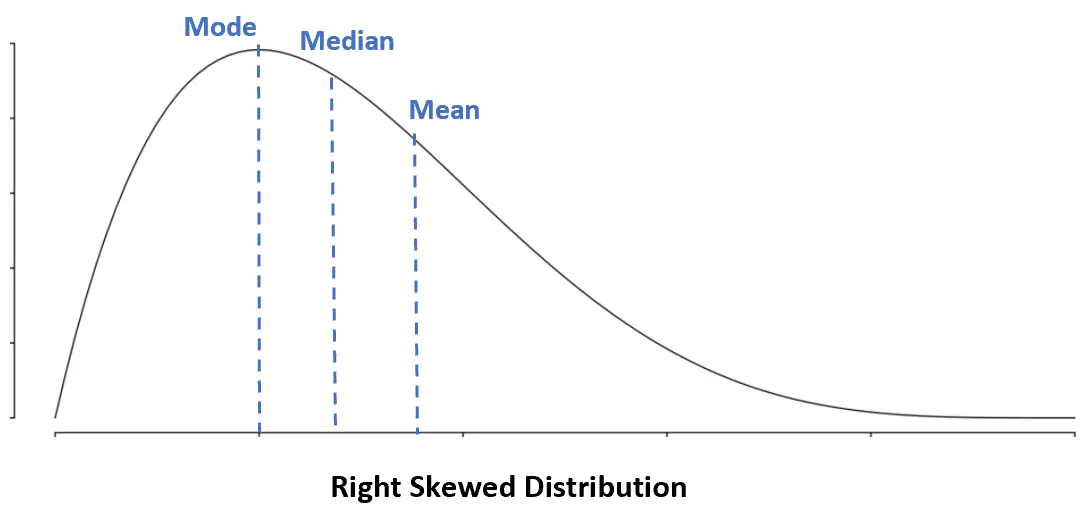
右に歪んだ分布では、平均値は中央値よりも大きくなります。
偏りなし:平均値 = 中央値 = 最頻値

対称分布では、平均、中央値、最頻値はすべて等しいです。