単純なランダムサンプリング

によるベンジャミン・アンダーソン博士 8月 6, 2023 統計 0コメント

この記事では、単純無作為標本とは何か、また単純無作為標本にはどのような種類があるのかを学びます。さらに、単純なランダムサンプリングがどのように実行されるかを例を通して説明します。最後に、単純なランダムサンプリングの長所と短所を確認できます。

単純ランダムサンプリングとは何ですか?

統計学において、単純無作為サンプリングは、研究用のサンプルを選択するために使用される確率的手法です。単純無作為抽出の主な特徴は、統計母集団の各要素が調査対象の標本に含まれる同じ確率を与えることです。

単純なランダムサンプリングでは、サンプル要素がランダムに選択されるため、結果として得られるサンプルは完全にランダムになります。

したがって、単純なランダムサンプリングを使用すると、特定のサンプルを取得する確率は、他のサンプルを取得する確率と等しくなります。この確率がどのように計算されるかを以下で見てみましょう。

サンプルから個人を選択する他の方法があることに留意してください。最もよく使用されるサンプリングのタイプは主に次のとおりです。

単純なランダムサンプリング
層化抽出法
体系的なサンプリング
集落抽出

単純なランダムサンプリングの概念は確かに理解するのが最も簡単なタイプですが、そのランダムな性質のため、実装が最も複雑であることが判明する場合があります。

単純なランダムサンプリングを行う方法

単純なランダムサンプリングを実行する手順は次のとおりです。

母集団のすべての要素を含むリストを作成します。
母集団の各要素に連続番号 (1、2、3、…、n) を割り当てます。
希望のサンプルサイズを設定します。
乱数発生器を使用して、選択したサンプルサイズと同じ数の数値を生成します。
生成された番号に割り当てられる個人は、サンプルの一部として選択された個人です。

乱数を生成するにはいくつかの方法がありますが、最も伝統的なのは宝くじ法とナンバーテーブル法です。

宝くじの方法では、すべての数字をボックスに入れてシャッフルし、ランダムに数字を引く必要があります。
数値テーブル法では、すべての可能な数値を含むテーブルからランダムに数値を選択します。

前の 2 つの方法のいずれかを使用することもできますが、これらはより多くの時間がかかるため、サンプルサイズが小さい場合に適しています。現在、乱数をより高速に生成するためにコンピュータープログラムが使用されています。たとえば、Excel プログラムを使用できます。

一方、サンプリング誤差を最小限に抑えるためには、サンプルサイズが適切である必要があることを考慮する必要があります。理想的なサンプルサイズを見つけるのは簡単ではありません。これについて疑問がある場合は、当社の Web サイトでその方法を説明した記事を検索してください。

単純なランダムサンプリングの例

単純なランダムサンプリングの定義を理解すると、このタイプのサンプリングがどのように実行されるかについての解決例がわかります。

たとえば、企業に 2,000 人の従業員がいて、400 人の従業員のサンプルを使用して統計調査を実行し、単純なランダムサンプリングでサンプルの一部となる個人を選択したい場合、最初に行うことは次のとおりです。各従業員に 1 から 2000 までの番号を割り当てます。

番号を割り当てた後、400 個の番号をランダムに選択する必要があります。この場合、サンプルサイズが非常に大きいため、Excelなどのコンピュータソフトウェアを使用するのが最適です。

次に、研究に参加するために選択された 400 人の労働者は、前のステップで割り当てられた番号が決定された労働者になります。

この例では、400 項目が十分に代表的なサンプルサイズであると考えられていますが、論理的にはこの数は実験に応じて変化します。

単純なランダムサンプリングの種類

単純なランダムサンプリングには 2 つのタイプがあります。

置換を伴う単純なランダムサンプリング: サンプリングフレームの選択された要素が返され、再度選択できます。
置換なしの単純なランダムサンプリング: サンプルの一部として選択されたアイテムは削除され、選択できなくなります。

置換を伴う単純なランダムサンプリングは、サンプルから項目を選択するためにまったく同じプロセスが常に繰り返されるため、最も単純なタイプのサンプリングです。ただし、置換を行わない単純なランダムサンプリングの方が精度が高いため、より広く使用されています。両方のタイプについては、以下で詳しく説明します。

置換を伴う単純なランダムサンプリング

置換を伴う単純なランダムサンプリングでは、選択された各項目をサンプリングフレームに戻して、それを再び選択する可能性が存在します。

したがって、明らかに可能性は非常に低いですが、1 つの項目を複数回選択したサンプルを取得することは可能です。

数学的には、各抽出の確率が同じであるため、これは非常に単純なタイプのサンプリングです。このため、他の人よりも先にこのサンプリング手法の研究を開始するのが通常です。

置換を伴う単純なランダムサンプリングでは、特定の順序でサンプルを取得する確率は、次の式を使用して計算できます。

$P=\cfrac{1}{N^n}$

なれ

$N$

母集団の要素の総数と

$n$

実行される独立した抽出の数。

一方、順序を問わない場合、サンプルが得られる確率は次の式で計算されます。

$P=\cfrac{n!}{\displaystyle N^n\prod_{i=1}^z k_i!}$

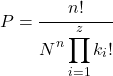
金

$n$

は独立した抽出の数、

$z$

サンプル内のさまざまな元素の数と

$k_i$

アイテムを何回表示したいか

$i$

サンプルで。

最後に、元素が含まれる確率を求めます。

$i$

、つまり要素が含まれる確率

$i$

この例では、次の式を使用する必要があります。

$\displaystyle \pi_i=1-\left(1-\frac{1}{N}\right)^n$

非置換の単純なランダムサンプリング

非置換の単純なランダムサンプリングでは、必要なサンプルサイズが示すとおり多くの個人をサンプルから選択する必要があり、各個人は一度選択されると再度選択することができません。したがって、選択した各項目は削除され、置き換えられません。

単純無作為抽出について話すときは、実際に最もよく使用される抽出であるため、通常、個人を入れ替えない抽出を指します。

置換を伴う単純なランダムサンプリングで特定の順序でサンプルを取得する確率を決定するには、次の式が使用されます。

$P=\cfrac{1}{n!\begin{pmatrix}N\\n\end{pmatrix}}$

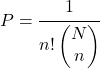
なれ

$N$

母集団内の要素の総数と

$n$

実行する依存抽出の数。

一方、抽出順序を考慮する必要がない場合、サンプルを取得する確率は次のようになります。

$P=\cfrac{1}{\begin{pmatrix}N\\n\end{pmatrix}}$

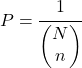
最後に、置換なしの単純なランダムサンプリングに要素が含まれる確率は、ラプラスの法則を適用して計算されます。

$\displaystyle \pi_i=\frac{n}{N}$

単純なランダムサンプリングの長所と短所

単純なランダムサンプリングには次のような利点と欠点があります。

アドバンテージ	短所
わかりやすい。	母集団のすべての要素のリストが必要です。
すべての可能なサンプルは等確率です。	サンプルサイズが大きい場合、これは非常にコストがかかる可能性があります。
通常、代表的なサンプルが得られます。	サンプリング誤差が大きくなる傾向があります。
サンプリングを実行するのに技術的な知識は必要ありません。	研究者が研究対象分野に関して持っているかもしれない知識は活用されません。
平均と偏差をすばやく計算できます。	サンプルが小さすぎると、代表的ではない可能性があります。
データを分析するための統計ソフトウェアがあります。	個別の面接が必要な研究には適していません。

これまで見てきたように、単純無作為抽出の主な特徴の 1 つは、理解と説明が簡単であることです。実際、サンプリングを実行する人は分析分野の専門家である必要はありません。ただし、他のタイプのサンプリングでは分析者の知識を活用してより良いサンプリングを実現できるため、これは長所でもあり短所でもあります。

同様に、他のタイプのサンプリングとは異なり、サンプリングはランダムであるため、調査対象のサンプルを構成するために特定の要素が採用される確率は等確率です。

通常、母集団の代表的なサンプルが取得されますが、単純なランダムサンプリングのサンプリング誤差は他のタイプのサンプリングと比較して大きくなります。さらに、個人のサイズが小さい場合、サンプルは代表的でさえない可能性があります。

単純なランダムサンプリングの非常に魅力的な特性は、コンピュータープログラムを使用して実行できることであり、統計計算を迅速に実行できることです。

最後に、単純なランダムサンプリングは、研究により多くのリソースの使用が必要になる可能性があるため、特に広範囲に分散した母集団の場合、他のタイプのサンプリングよりも費用がかかる可能性があることに注意する必要があります。たとえば、無作為抽出であるため、研究を実施するために選ばれた人々は地理的に広範囲に分散している可能性があり、そのため対面でのインタビューの実施にははるかに費用がかかります。

著者について

ベンジャミン・アンダーソン博士

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る