単純な線形回帰

この記事では、統計における単純線形回帰とは何か、またその実行方法について説明します。同様に、単純な線形回帰の演習が解決され、さらに、単純な線形回帰計算ツールがオンラインで見つかります。

単純線形回帰とは何ですか?

単純線形回帰は、独立変数を関連付けるために使用される統計モデルであり、2 つの変数の間にある関係を近似しようとします。

したがって、単純な線形回帰を使用して、2 つの変数を線形に関連付ける方程式を見つけます。論理的には、2 つの変数間の関係は線形でなければなりません。そうでない場合は、別のタイプの回帰モデルを使用する必要があります。

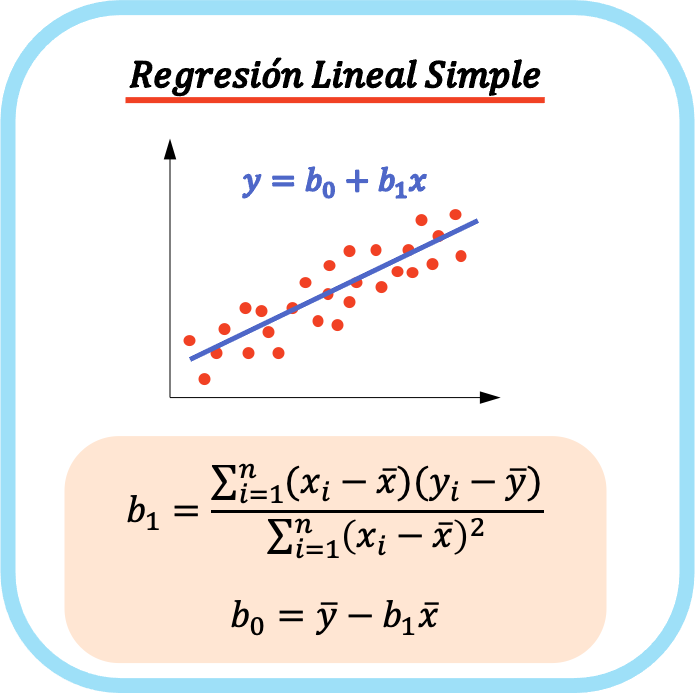
単純な線形回帰モデルの方程式は、方程式の定数 (b ₀ ) と 2 つの変数間の相関係数 (b ₁ ) の 2 つの係数で構成されます。したがって、単純な線形回帰モデルの方程式は y=b ₀ +b ₁ x となります。

単純な線形回帰の式は直線としてグラフ化されるため、係数 b ₀は切片、係数 b ₁は直線の傾きになります。

単純な線形回帰式

単純な線形回帰の係数を計算する式は次のとおりです。

👉以下の計算機を使用して、任意のデータセットの単純線形回帰の係数を計算できます。

単純な線形回帰モデルから得られる方程式では、すべての観測値の正確な値を推測することはできません。これは、このモデルが単に 2 つの変数間の関係を近似する方程式を見つけようとするだけであるためです。したがって、残差は、真の値と線形回帰モデルによって推定された値との差として定義されます。

単純な線形回帰モデルの目標は、残差の二乗を最小化することです。つまり、単純な線形回帰は最小二乗基準に基づいています。

単純な線形回帰の具体例

単線形回帰法の理解を完了するために、一連の統計データから単線形回帰モデルの方程式を計算する実際的な例を段階的に示します。

• 統計試験を受けた後、5 人の学生に、試験に費やした勉強時間について尋ねました。データを以下の表に示します。収集した統計データの単純な線形回帰モデルを実行して、学習時間と達成した成績を線形に関連付けます。

単純な線形回帰モデルを実行するには、方程式の係数 b ₀と b ₁を決定する必要があり、そのためには、上のセクションで説明した式を使用する必要があります。

ただし、単純な線形回帰式を適用するには、まず独立変数の平均と従属変数の平均を計算する必要があります。

変数の平均がわかったので、対応する式を使用してモデルの係数 b ₁を計算します。

最後に、対応する式を使用してモデルの係数 b ₀を計算します。

つまり、この問題の単純な線形回帰モデルの方程式は次のとおりです。

以下に、サンプル データのグラフ表現と単純な線形回帰モデルの直線を示します。

最後に、単純な線形回帰モデルの方程式を計算したら、あとは得られた結果を解釈するだけです。このためには、回帰モデルの決定係数を計算することが不可欠です。これがどのように行われるかは、当社の Web サイトで対応する記事を検索することで確認できます。

単純な線形回帰の仮定

単純な線形回帰を実行するには、次の前提を満たす必要があります。

• 独立性: 観察される残基は互いに独立している必要があります。モデルの独立性を確保する一般的な方法は、サンプリング プロセスにランダム性を追加することです。
• 等分散性: 残差の分散には均一性がなければなりません。つまり、残差の変動性は一定でなければなりません。
• 正規性: 残差は正規分布する必要があります。つまり、残差は平均 0 の正規分布に従う必要があります。
• 線形性– 独立変数と従属変数の間の関係は線形である必要があります。

単純な線形回帰計算機

サンプル データを以下の計算機に接続して、2 つの変数間の単純な線形回帰モデルを当てはめます。最初のボックスには独立変数 X の値のみが含まれ、2 番目のボックスには従属変数 Y の値のみが含まれるように、データのペアを分離する必要があります。

データはスペースで区切られ、小数点としてピリオドを使用して入力する必要があります。

単純な重回帰

最後に、単純線形回帰と多重線形回帰の違いについて説明します。これらは統計で頻繁に使用される 2 種類の線形回帰です。

多重線形回帰を使用すると、 2 つ以上の説明変数を応答変数に数学的に関連付けることができます。つまり、重線形回帰では、少なくとも 2 つの独立変数が存在するモデルが作成されます。

したがって、単純線形回帰と多重線形回帰の違いは独立変数の数です。単回帰では独立変数は 1 つだけですが、重線形回帰では独立変数は 2 つ以上あります。