単調な関係とは何ですか? (定義 + 例)
統計学では、2 つの変数間の単調な関係とは、通常、1 つの変数の変化が別の変数の特定の方向の変化に関連付けられるシナリオを指します。
単調関係には 2 つのタイプがあります。
正の単調性: 1 つの変数の値が増加すると、他の変数の値も増加する傾向があります。
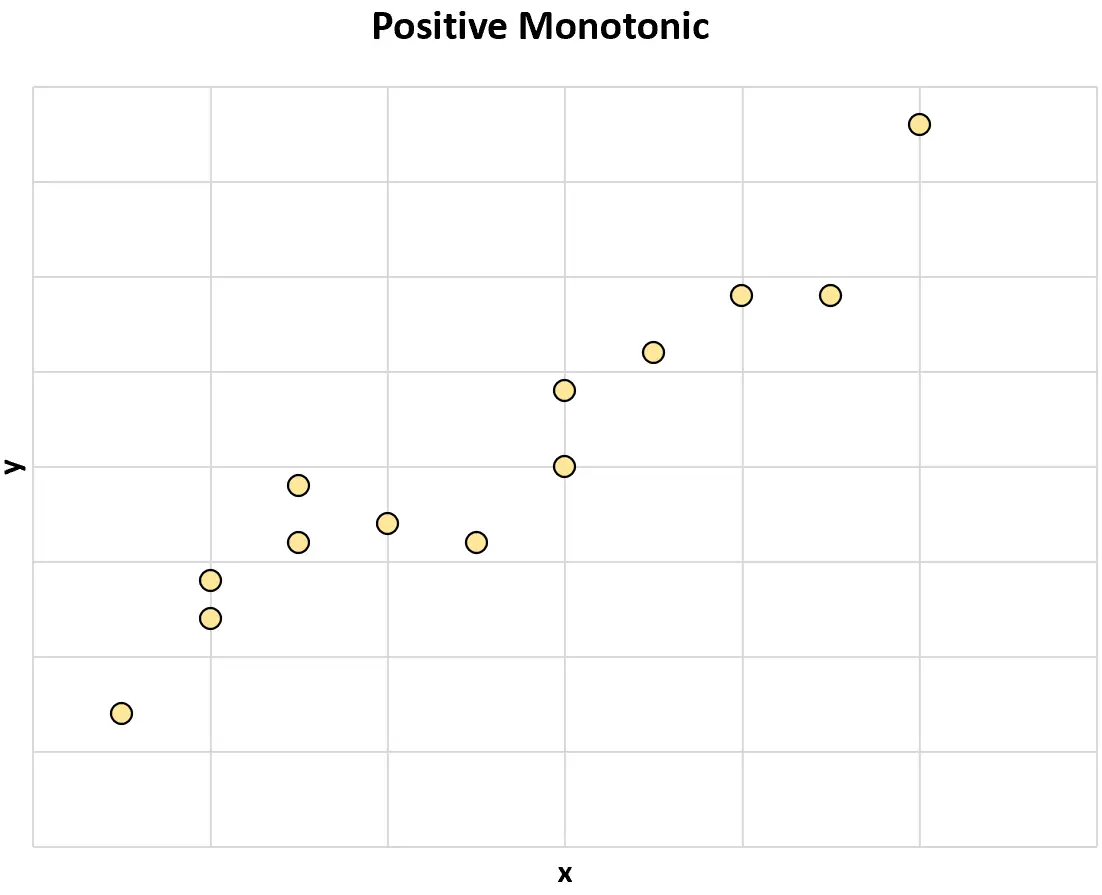
負の単調性: 1 つの変数の値が増加すると、もう 1 つの変数の値は減少する傾向があります。
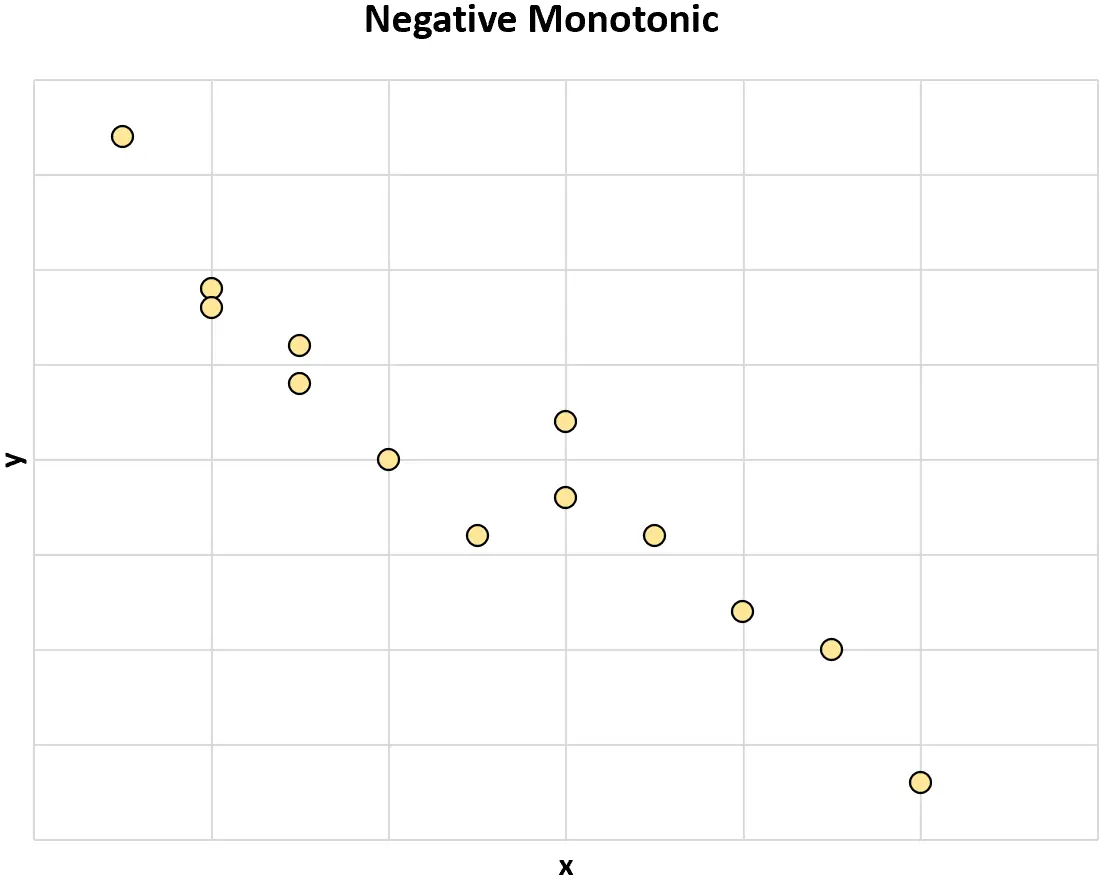
2 つの変数が一般に同じ方向に変化しない場合、それらは非単調な関係があると言われます。
2 つの変数間の非単調な関係の例を次に示します。
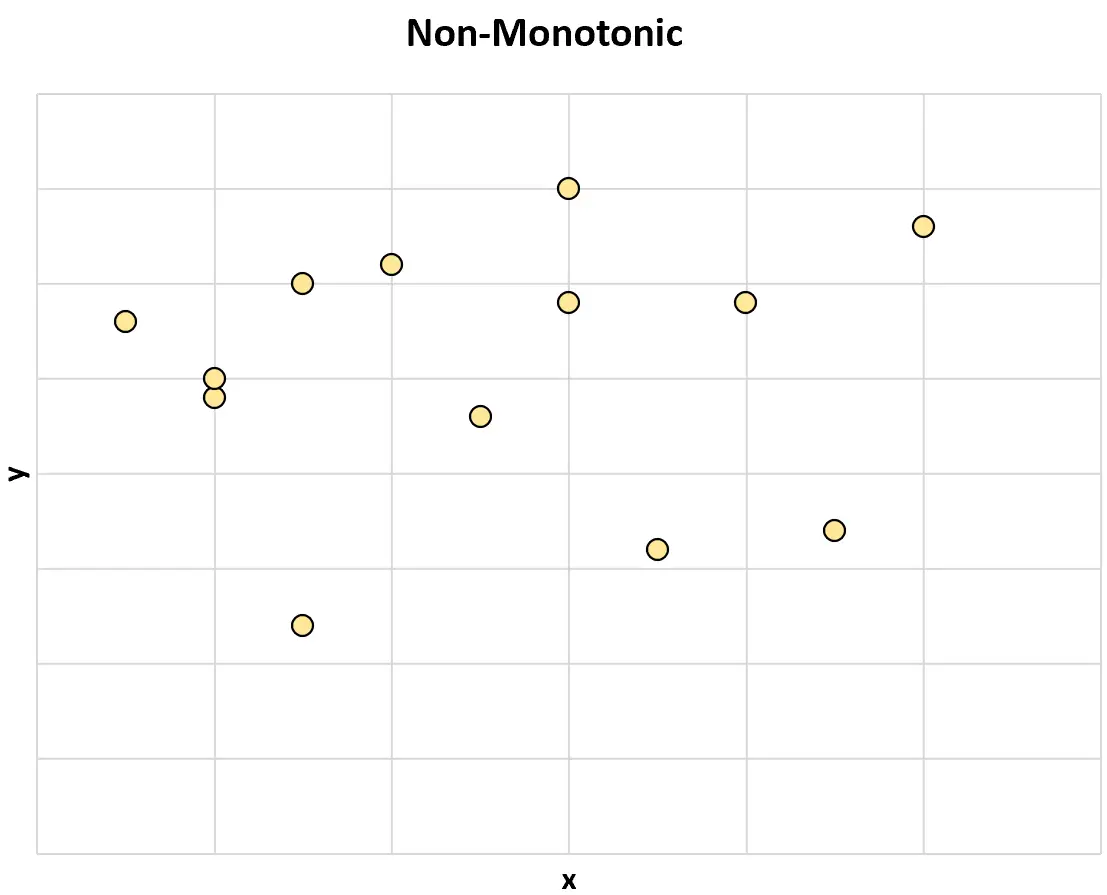
次に、2 つの変数間の非単調な関係の別の例を示します。
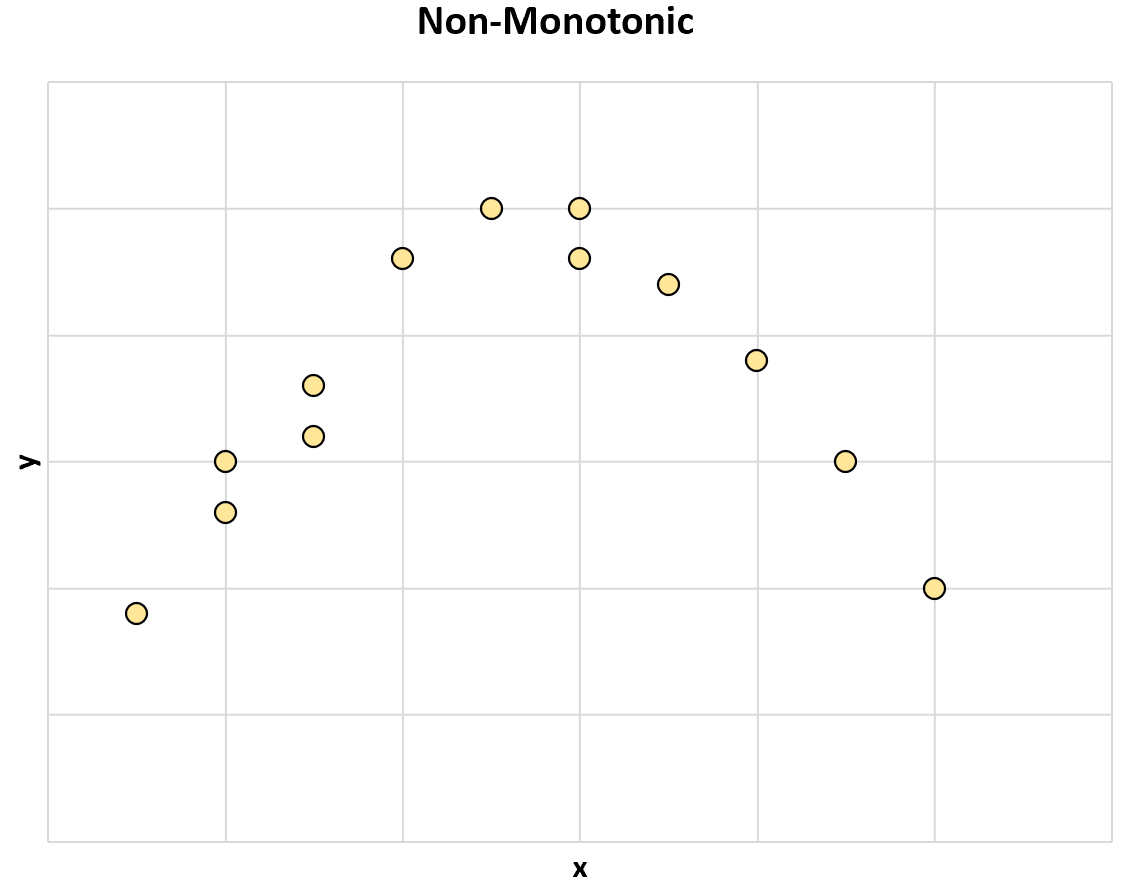
x の値が増加すると、y の値が増加する場合もありますが、y の値が減少する場合もあります。
厳密に単調であるか、厳密には単調ではない
1 つの変数の変化が常に別の変数の同じ方向の変化に関連付けられている場合、2 つの変数は厳密に単調な関係にあると言われます。
たとえば、次のグラフは、2 つの変数間の厳密に正の単調関係を示しています。
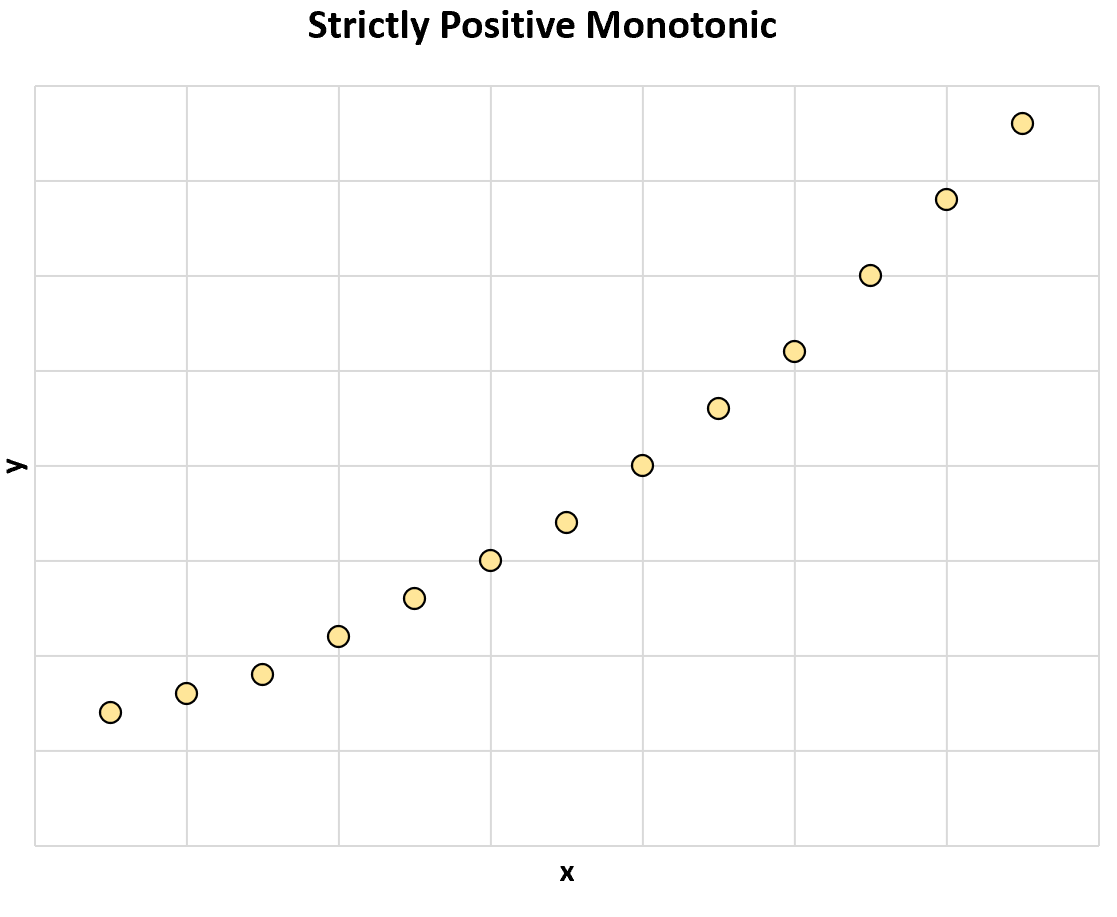
x の値が増加すると、y の値も常に増加します。
次のグラフは、2 つの変数間の厳密に負の単調関係を示しています。
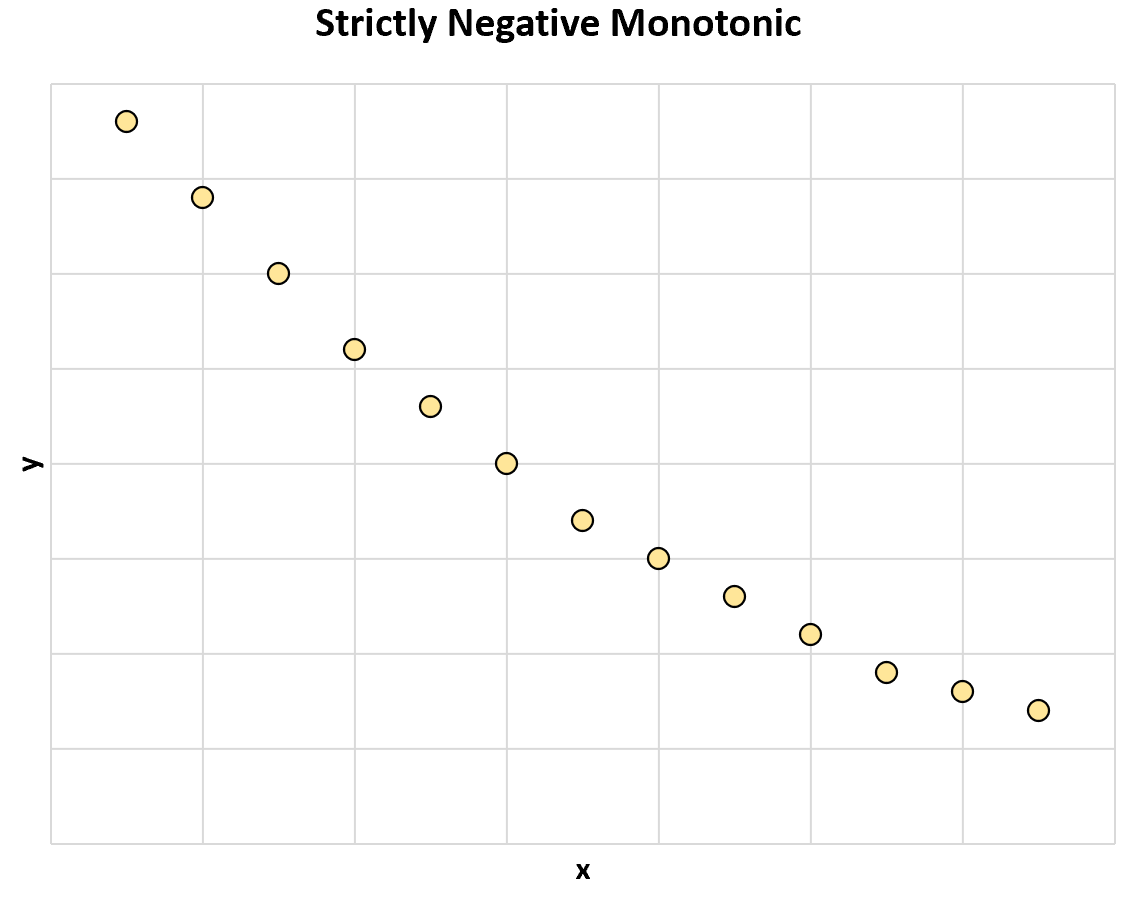
x の値が増加すると、y の値は常に減少します。
単調な関係を定量化する方法
2 つの変数間の関係を定量化する最も一般的な方法は、2 つの変数間の線形関連性を測定するピアソン相関係数を使用することです。
この係数は常に -1 から 1 までの値を取ります。
- -1 は、2 つの変数間の完全な負の線形相関を示します。
- 0 は 2 つの変数間に線形相関がないことを示します
- 1 は、2 つの変数間の完全な正の線形相関を示します。
係数が 1 に近づくほど、2 つの変数間の正の関係が強くなります。逆に、係数が -1 に近づくほど、2 つの変数間の負の関係が強くなります。
ただし、2 つの変数間の関係が単調であるものの非線形である場合 (指数関係など)、単調関係を適切に処理するように設計されたSpearman Rank correlationを使用することをお勧めします。
計算する相関係数の種類に関係なく、散布図を作成して変数間の関係も視覚化することをお勧めします。