反復測定分散分析の 3 つの仮定

反復測定 ANOVA は、各グループに同じ被験者が含まれる 3 つ以上のグループの平均間に統計的に有意な差があるかどうかを判断するために使用されます。

ただし、反復測定 ANOVA を実行する前に、次の前提条件が満たされていることを確認する必要があります。

1. 独立性:各観測は独立している必要があります。

2. 正規性:応答変数の分布は正規分布します。

3. 球形性:関連するグループのすべての組み合わせ間の差の分散は等しくなければなりません。

これらの仮定の 1 つ以上が違反される場合、反復測定 ANOVA の結果は信頼できない可能性があります。

この記事では、各前提の説明、前提が満たされているかどうかを判断する方法、満たされていない場合の対処方法について説明します。

仮説 1: 独立性

反復された ANOVA 測定では、データ セット内の各観測値が他のすべての観測値から独立していると想定されます。

この仮定が満たされているかどうかを判断する方法

この仮定を検証する最も簡単な方法は、データセット内の各個人が ランダム サンプリング法を使用して 母集団からランダムに抽出されたことを検証することです。

ランダムなサンプリング方法が使用された場合、各観測値は独立していると想定できます。

この前提が尊重されない場合はどうすればよいか

この仮定が満たされない場合、各個人の価値観は何らかの形で相互に関連している可能性があるため、深刻な問題になります。

多くの場合、このシナリオでの唯一の解決策は、無作為抽出法を使用して新しい研究のために個人を募集することです。

仮説 2: 正常性

反復された ANOVA 測定では、応答変数の分布が正規分布していると仮定されます。

この仮定が満たされているかどうかを判断する方法

この仮説が正しいかどうかを確認するには、次の 2 つの方法があります。

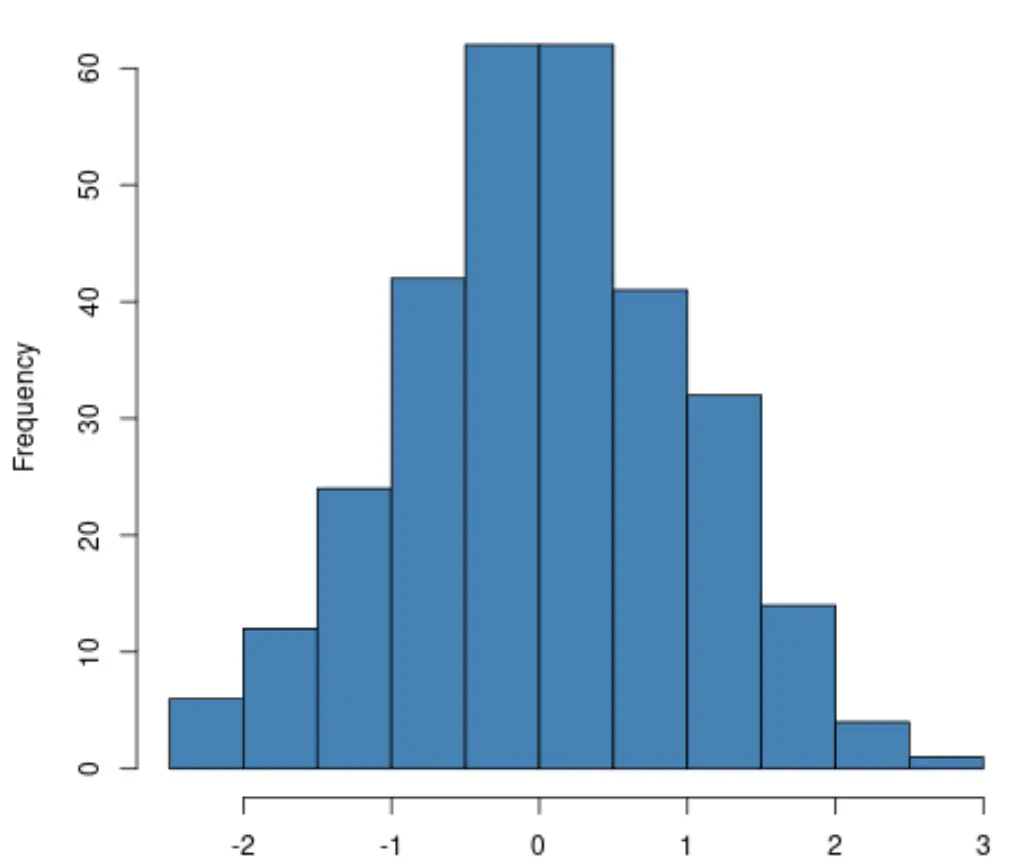
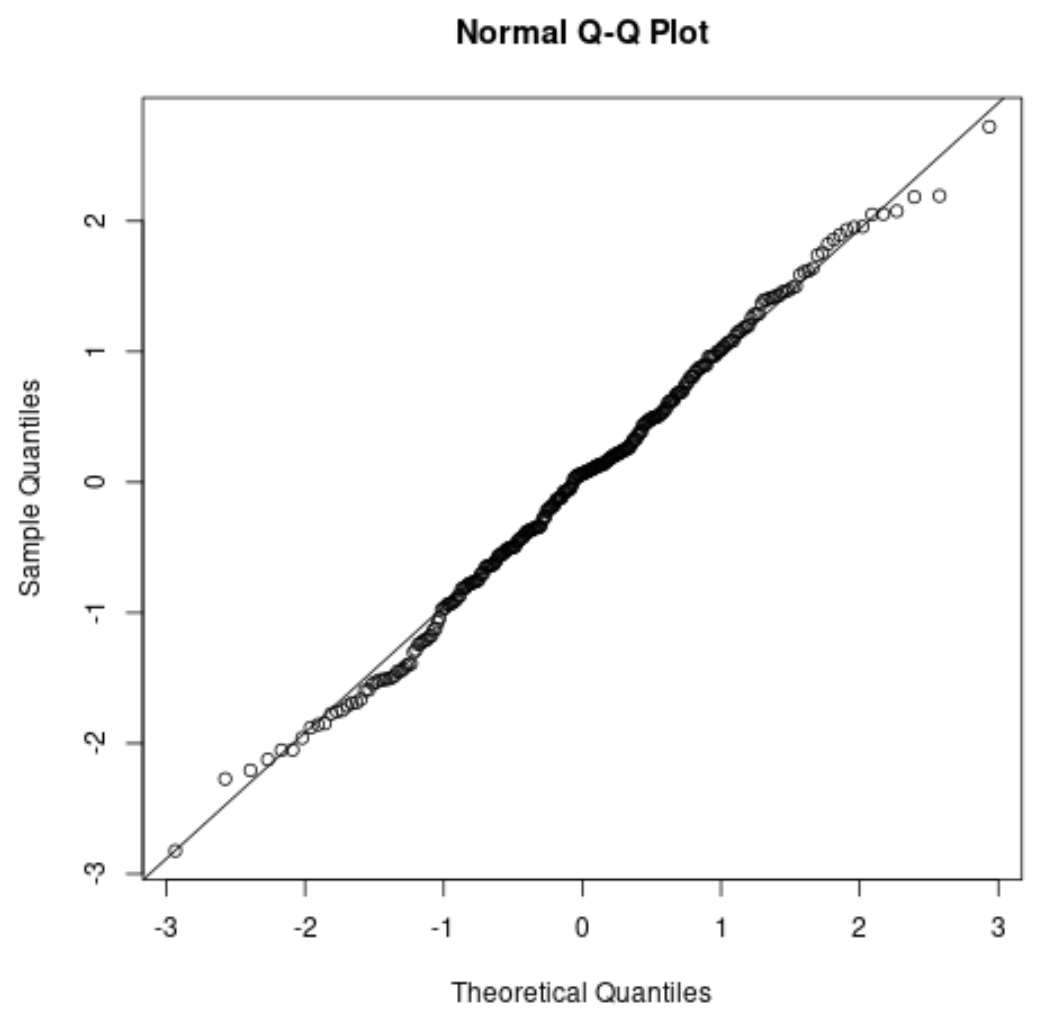
1. ヒストグラムまたは QQ プロットを作成する

ヒストグラムまたは QQ プロットを作成すると、応答変数の分布がほぼ正規分布しているかどうかを視覚的に確認できます。

ヒストグラムを作成する場合は、応答変数の分布がほぼ「ベル」形状に従っていることを確認するだけです。そうであれば、多くの場合、正規性の仮定が満たされていると想定できます。

QQ プロットを作成している場合は、データ ポイントが直線の対角線に沿って配置されているかどうかを確認してください。そうであれば、通常は正規性の仮定が満たされていると想定できます。

関連: QQ プロットを使用して正規性をチェックする方法

2. 正式な統計テストを実行する

Shapiro-Wilk テストを実行して正規性を確認することもできます。検定のp 値が 0.05 未満の場合、データが正規分布していないことを示します。

ただし、非常に大規模なサンプルを扱う場合、Shapiro-Wilk テストのような統計テストでは、ほとんどの場合、データが正規ではないことが示されることに注意してください。

このため、多くの場合、ヒストグラムや QQ プロットなどのグラフを使用してデータを視覚的に検査することが最善です。グラフを見るだけで、データが正規分布しているかどうかをかなり理解できます。

この前提が尊重されない場合はどうすればよいか

一般に、反復測定 ANOVA は、サンプル サイズが十分に大きい限り、正規性の仮定の違反に対して非常に堅牢であると考えられます。

正規性の仮定が著しく違反されている場合、選択肢は 2 つあります。

1.分布がより正規分布になるように、データの応答値を変換します。

2.正規性の仮定を必要としない フリードマン テストなどの同等のノンパラメトリック テストを実行します。

仮定 3: 真球度

反復測定 ANOVA は球形性を前提としています。つまり、関連するグループのすべての組み合わせの間の差の分散は等しい必要があります。

この仮定が満たされない場合、F 比が膨張し、反復測定 ANOVA の結果の信頼性が低くなります。

この仮定が満たされているかどうかを判断する方法

この仮定が満たされるかどうかをテストするために、Mauchly の球形性テストを実行できます。

この検定では、次の帰無仮説と対立仮説を使用します。

• H ₀ : 差の分散は等しい
• H _A : 差の分散は等しくない

検定の p 値が特定の有意水準(例: α = 0.05) を下回っている場合、帰無仮説は棄却され、差の分散は等しくないと結論付けられます。

それ以外の場合、p 値が特定の有意レベル (たとえば、α = 0.05) を下回らない場合、帰無仮説を棄却できず、球面性の仮定が満たされていると結論付けられます。

使用する統計ソフトウェアに応じて、このテストの結果は次のようになります。

p 値は 0.05 未満ではないため、帰無仮説を棄却できず、この特定の例では球形性の仮定が満たされていると結論付けられます。

この前提が尊重されない場合はどうすればよいか

Mauchly の球形性検定の帰無仮説を棄却する場合、通常、反復測定 ANOVA テーブルの F 値の計算に使用される自由度に補正を適用します。

適用できる修正は 3 つあります。

• Huynh-Feldt (最も保守的ではない)
• セール・ガイザー
• 下限値 (最も保守的な値)

これらの各補正は、球形性の仮定に違反しているという事実を考慮して、反復測定 ANOVA 出力テーブルの p 値を増加させる傾向があります。

これらの p 値を使用して、反復測定 ANOVA の帰無仮説を棄却する必要があるかどうかを判断できます。

追加リソース

次のチュートリアルでは、反復測定 ANOVA に関する追加情報を提供します。

反復測定 ANOVA の概要
反復測定 ANOVA 計算機
反復測定 ANOVA の結果を報告する方法
一元配置分散分析と反復測定分散分析: 違い