同時確率分布とは何ですか?
双方向度数表は、 2 つのカテゴリ変数の頻度 (または「カウント」) を表示する表です。
たとえば、次の二元表は、100 人に野球、バスケットボール、サッカーのどのスポーツが好きかを尋ねたアンケートの結果を示しています。
行には回答者の性別が表示され、列には回答者が選択したスポーツが表示されます。

この例には、スポーツとジェンダーという 2 つの変数があります。
同時確率分布は、特定の個人が変数に対して 2 つの特定の値を取る確率を単純に表します。
「結合」という言葉は、2 つのことが同時に起こる確率に興味があるという事実に由来しています。
たとえば、合計 100 人のうち 13 人が男性で、好きなスポーツとして野球を選択しました。
したがって、特定の個人が男性で、好きなスポーツとして野球を選択する同時確率は 13/100 = 0.13または13%であると言えます。
数学的表記法で書くと次のようになります。
P(性別 = 男性、スポーツ = 野球) = 13/100 = 0.13 。
このプロセスを使用して、同時確率分布全体を計算できます。
- P (性別 = 男性、スポーツ = 野球) = 13/100 = 0.13
- P(性別 = 男性、スポーツ = バスケットボール) = 15/100 = 0.15
- P(性別 = 男性、スポーツ = サッカー) = 20/100 = 0.20
- P (性別 = 女性、スポーツ = 野球) = 23/100 = 0.23
- P(性別 = 女性、スポーツ = バスケットボール) = 16/100 = 0.16
- P(性別 = 女性、スポーツ = サッカー) = 13/100 = 0.13
確率の合計は1 、つまり100%に等しいことに注意してください。
なぜ同時確率分布を使用するのでしょうか?
同時確率分布は、2 つの変数 (スポーツと性別など) のデータを収集することが多く、両方の変数に関連する質問に答えたい場合に便利です。
たとえば、 母集団内の特定の個人が男性で、好きなスポーツとして野球を好む確率を理解したい場合があります。
あるいは、特定の個人が女性で、好きなスポーツとしてサッカーを好む確率を理解することに興味があるかもしれません。
同時確率分布は、これらの質問に答えるのに役立ちます。
同時確率分布をより深く理解するための練習として、次の例を使用してください。
例1
次の二元表は、238 人にどのような種類の映画が好きかを尋ねたアンケートの結果を示しています。
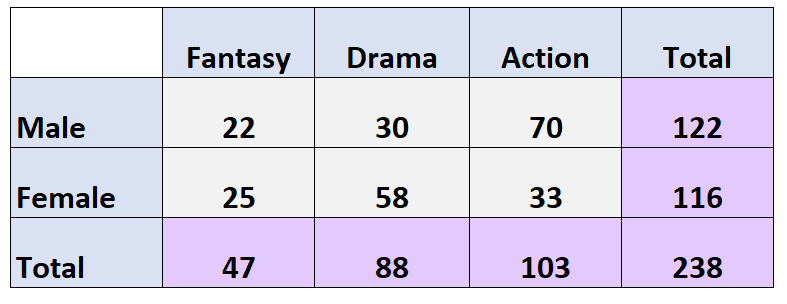
質問:特定の個人が女性で、好きな映画ジャンルとしてドラマを好む確率はどれくらいですか?
答え: P (性別 = 女性、性別 = ドラマ) = 58/238 = 0.244 = 24.4%
例 2
次の二元表は、クラスの 64 人の生徒の試験の得点を、勉強に費やした時間数に基づいて示しています。
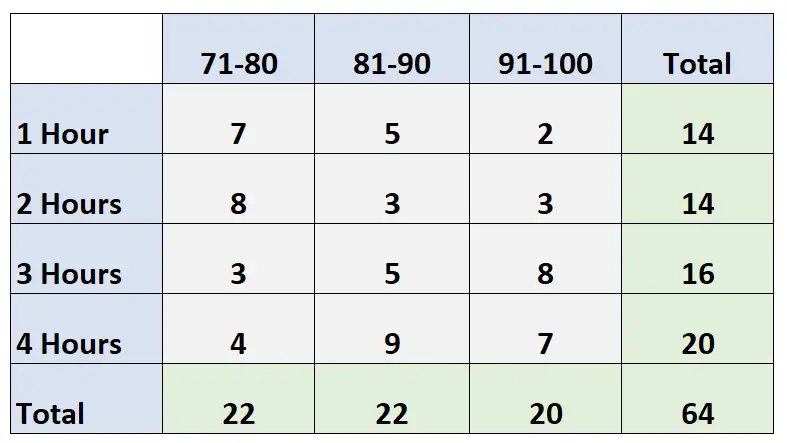
質問:特定の個人が 2 時間勉強して 91 ~ 100 点の成績を獲得する確率はどれくらいですか?
答え: P (学習時間 = 2 時間、スコア = 91-100) = 3/64 = 0.047 = 4.7%