四分位数

によるベンジャミン・アンダーソン博士 8月 5, 2023 統計 0コメント

この記事では、四分位とは何かについて説明します。各四分位の定義、計算方法、およびいくつかの具体例が示されています。グループ化されたデータの四分位を計算する方法も示します。さらに、オンライン計算機を使用して、任意のデータセットの四分位を計算できます。

四分位数とは何ですか?

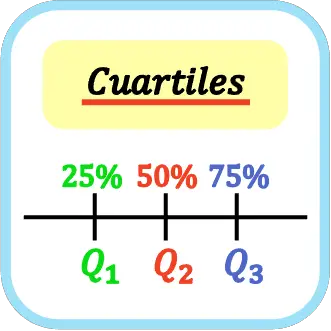
統計において、四分位とは、順序付けされたデータのセットを 4 つの等しい部分に分割する 3 つの値です。したがって、第 1 四分位、第 2 四分位、および第 3 四分位は、それぞれ、すべての統計データの 25%、50%、および 75% を表します。

四分位は大文字の Q と四分位インデックスで表されるため、最初の四分位は Q ₁ 、2 番目の四分位は Q ₂ 、そして 3 番目の四分位は Q ₃となります。

👉以下の計算機を使用して、任意のデータセットの四分位を計算できます。

四分位数は、五分位数、十分位数、パーセンタイル数と同様に、中心以外の位置の尺度であることに注意してください。この Web ページで、これらの分位数の種類がそれぞれ何であるかを確認できます。

最初の四分位

最初の四分位(四分位 1 とも呼ばれます) は、サンプル内の統計データの 25% を超える値です。言い換えれば、最初の四分位は観測データの 25% 以上を表します。

最初の四分位は記号 Q ₁で表され、サンプル内の最小のデータ値を示すために使用されます。

第 2 四分位

2 番目の四分位(四分位 2 とも呼ばれます) は、サンプル内の統計データの 50% を超える値です。したがって、第 2 四分位はデータセットを 2 つの半分に分割し、中央値と第 5 十分位数に一致します。

第 2 四分位の記号は_Q2です。

第3四分位

第3 四分位(第 3 四分位とも呼ばれます) は、サンプル内の統計データの 75% を超える値です。言い換えれば、第 3 四分位は収集されたデータの 75% 以上を占めます。

3 番目の四分位は記号 Q ₃で表され、サンプル内の最大値を表します。

四分位数の計算方法

統計データセットの四分位数の位置を計算するには、四分位数にデータの総数に 1 を加えた合計を乗算し、その結果を 4 で割る必要があります。

したがって、四分位数の式は次のようになります。

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

注:この式は、四分位の値ではなく、四分位の位置を示します。四分位は計算式で求めた位置にあるデータとなります。

ただし、この式の結果から 10 進数が得られる場合があります。したがって、結果が 10 進数であるかどうかに応じて 2 つのケースを区別する必要があります。

式の結果が小数部のない数値である場合、四分位は上記の式で指定された位置にあるデータです。
数式の結果が小数部を含む数値である場合、四分位値は次の数式を使用して計算されます。

$Q=x_i+d\cdot (x_{i+1}-x_i)$

ここで、x _iおよびx _i+1は、最初の式で得られた数値が挟まれる位置の番号であり、 dは、最初の式で得られた数値の小数部分です。

さて、四分位数の計算は、考慮すべきことがたくさんあるため、非常に複雑になるかもしれません。しかし、次のセクションの 2 つの例を見ると、実際には非常に簡単であることがわかります。

注: 科学界では、四分位数の計算方法について合意が得られていないため、少し異なる方法で説明している統計の本を見つけることができます。

四分位数の計算例

四分位数の計算方法を完全に理解するには、以下の 2 つの解決済み演習を参照してください。最初の四分位数は整数であり、二番目の四分位数は 10 進数であるため、どの 2 つのケースが見つかるかがわかります。

例1

次のデータセットの 3 つの四分位数を計算します。

上で見たように、四分位数を決定する式は次のとおりです。

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

この場合、 n 、観測値の合計数は 15 であるため、最初の四分位を見つけるには、 nを 15 に、 kを 1 に置き換える必要があります。

$\cfrac{1\cdot (15+1)}{4}=4 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad Q_1=39$

したがって、最初の四分位は、値の順序付きリストの 4 番目の数値であり、この場合は 39 です。

同様に、係数k を2 に置き換えて 2 番目の四分位を計算します。

$\cfrac{2\cdot (15+1)}{4}=8 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad Q_2=48$

したがって、四分位 2 は並べ替えられたリストの 8 番目の数値であり、値 48 に対応します。

最後に、 k =3 として式をもう一度適用して、第 3 四分位を計算します。

$\cfrac{3\cdot (15+1)}{4}=12 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad Q_3=60$

四分位 3 は 12 番目の位置、つまり 60 のデータに対応します。

例 2

次のデータ系列の 3 つの四分位を見つけます。

この 2 番目の例では、観測値が 24 個あるため、四分位数式から得られる数値は 10 進数になります。

まず、一般式の 1 をkに置き換えて、最初の四分位の位置を計算します。

$\cfrac{k\cdot (n+1)}{4}$

$\cfrac{1\cdot (24+1)}{4}=6,25$

しかし、10 進数 6.25 が得られたため、最初の四分位は 6 番目と 7 番目のデータ (それぞれ 22 と 25) の間にあります。したがって、正確な四分位を計算するには、次の式を適用する必要があります。

$Q=x_i+d\cdot (x_{i+1}-x_i)$

この場合、 x _iは 22、 x _i+1 25、 dは得られた数値の小数部分、つまり 0.25 です。まだ：

$Q_1=22+0,25\cdot (25-22)=22,75$

次に、同じ手順を実行して 2 番目の四分位を見つけます。

$\cfrac{2\cdot (24+1)}{4}=12,5$

再度、数式から 10 進数を取得します。この場合は 12.5 です。したがって、データテーブルの 12 番目と 13 番目の数値 (49 と 50 に対応) に対して同じ式を使用する必要があります。

$Q_2=49+0,5\cdot (50-49)=49,5$

最後に、同じプロセスを繰り返して 3 番目の四分位を取得します。

$\cfrac{3\cdot (24+1)}{4}=18,75$

ただし、数値 18.75 は数値 18 と 19 の間にあるため、第 3 四分位はこれらの位置 (71 と 73) の値の間にあります。より正確には、これは次の式から得られる値になります。

$Q_3=71+0,75\cdot (73-71)=72,5$

四分位計算機

統計データセットを以下の計算機に接続して、四分位を計算します。データはスペースで区切られ、小数点としてピリオドを使用して入力する必要があります。

グループ化されたデータの四分位数

データが間隔にグループ化されているときに四分位を計算するには、まず次の式を使用して、四分位が該当する間隔またはビンを見つける必要があります。

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

したがって、四分位は、絶対累積頻度が前の式で得られた数よりもすぐに大きい区間内にあります。

四分位が属する区間がわかったら、次の式を適用して四分位の正確な値を見つける必要があります。

$Q_k=L_i+ \cfrac{\displaystyle\frac{k\cdot (n+1)}{4}-F_{i-1}}{f_i}\cdot I_i \qquad k=1,2,3$

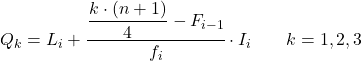
金：

L _{i は}、四分位が含まれる区間の下限です。
nは観測値の総数です。
F _i-1は、前の間隔の累積絶対頻度です。
f _iは、四分位が含まれる区間の絶対周波数です。
I _iは四分位区間の幅です。

例として、グループ化された一連のデータの四分位を計算する演習を次に示します。

最初の四分位を計算するには、まずそれが該当する間隔を決定する必要があります。これを行うには、次の式を適用します。

$\cfrac{k\cdot (n+1)}{4}$

$\cfrac{1\cdot (30+1)}{4} =7,75 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [50,60)$

したがって、最初の四分位は、累積絶対頻度が 7.75 よりすぐ大きい区間内にあります。この場合、それは累積絶対頻度が 15 である区間 [50.60) です。そして、四分位区間がわかったら、2 番目のプロセス公式を使用します。 :

$Q_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{4}-F_{i-1}}{f_i}\cdot I_i$

$Q_1=50+\cfrac{\displaystyle\frac{1\cdot (30+1)}{4}-7}{8}\cdot 10=50,94$

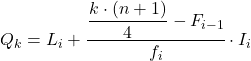
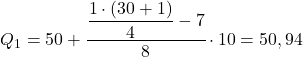
同じ手順を再度適用して、2 番目の四分位を取得します。まず、四分位が存在する間隔を決定します。

$\cfrac{2\cdot (30+1)}{4} =15,5 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [60,70)$

累積絶対頻度が 15.5 よりすぐ大きい区間は [60.70) で、累積絶対頻度は 26 です。したがって、第 2 四分位は次のようになります。

$Q_2=60+\cfrac{\displaystyle\frac{2\cdot (30+1)}{4}-15}{11}\cdot 10=60,45$

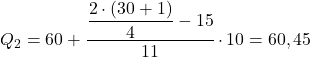
そして最後に、このプロセスを繰り返して、第 3 四分位を見つけます。まず、四分位を含む区間を計算します。

$\cfrac{3\cdot (30+1)}{4} =22,5 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [60,70)$

23.25 のすぐ上の累積絶対頻度は 26 であるため、第 3 四分位範囲は [60.70) です。したがって、次の式を適用して、この間隔で四分位を計算します。

$Q_3=60+\cfrac{\displaystyle\frac{3\cdot (30+1)}{4}-15}{11}\cdot 10=67,5$

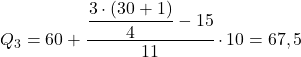
四分位数は何に使用されますか?

四分位数は位置の尺度であるため、データがどのように配置されているかを知るために使用されます。言い換えれば、3 つの四分位の値によって、サンプル内のランダムなデータ項目が非常に大きいか、非常に小さいか、あるいは平均値であるかを知ることができます。

サンプルからデータをランダムに取得した場合、四分位数と比較することで、その値が高いか低いかを知ることができます。ランダムデータ値が第 1 四分位より小さい場合は小さな値になりますが、その値が第 3 四分位より大きい場合は大きな値になります。同様に、前記データの値が第 1 四分位数と第 3 四分位数の間にある場合、それは中間値です。

一方、四分位は、四分位範囲 (または四分位範囲) などの他の統計的尺度を計算したり、箱ひげ図 (または箱ひげ図) などの図を作成するためにも使用されます。

著者について

ベンジャミン・アンダーソン博士

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る

四分位数とは何ですか?

最初の四分位

第 2 四分位

第3四分位

四分位数の計算方法

四分位数の計算例

例1

例 2

四分位計算機

グループ化されたデータの四分位数

四分位数は何に使用されますか?

著者について

ベンジャミン・アンダーソン博士

コメントを追加する