四分位範囲 (iqr) は外れ値の影響を受けますか?
統計では、値が分布内でどの程度の範囲に「分散」しているかを知りたいことがよくあります。
広がりを測定する一般的な方法は、データセットの第 1 四分位と第 3 四分位の差として計算される四分位範囲です。四分位数は、データセットを 4 つの等しい部分に分割する単純な値です。
例: 四分位範囲の計算
次の例は、特定のデータ セットの四分位範囲を計算する方法を示しています。
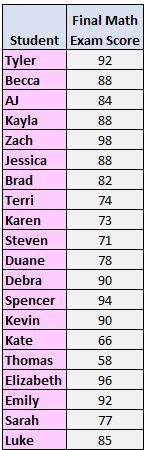
ステップ 1: 値を最小値から最大値の順に並べます。
58、66、71、73、74、77、78、82、84、85、88、88、88、90、90、92、92、94、96、98
2. 中央値を見つけます。
58、66、71、73、74、77、78、82、84、85、88、88、88、90、90、92、92、94、96、98 _
この場合、中央値は 85 ~ 88 になります。
3. 中央値はデータセットを 2 つに分割します。下半分の中央値は下四分位、上半分の中央値は上位四分位です。
58、66、71、73、74、77、78、82、84、85、88、88、88、90、90、92、92、94、96、98 _
4. 四分位範囲を計算します。
この場合、最初の四分位はデータ セットの下半分の中央の 2 つの値の平均 (75.5)、第 3 四分位はデータ セットの上半分の中央の 2 つの値の平均です。 (91)。
したがって、四分位範囲は 91 – 75.5 = 15.5となります。
四分位範囲は外れ値の影響を受けません
データセットの「広がり」を計算するときに四分位範囲 (IQR) を使用することを好む理由の 1 つは、IQR が外れ値に対して堅牢であるためです。 IQR は単にデータ値の中央の 50% 範囲であるため、 極端な外れ値の影響を受けません。
これを実証するには、次のデータセットを考えてみましょう。
[1、4、8、11、13、17、17、20]
このデータセットのさまざまな伝播メトリクスを次に示します。
- 四分位範囲: 11
- 範囲: 19
- 標準偏差: 6.26
- 差: 39.23
次に、同じデータセットを考慮しますが、極端な外れ値が追加されています。
[ 1、4、8、11、13、17、17、20、150 ]
このデータセットのさまざまな伝播メトリクスを次に示します。
- 四分位範囲: 12.5
- 範囲: 149
- 標準偏差: 43.96
- スプレッド: 1,932.84
四分位範囲が 11 から 12.5 までわずかに変化するだけであることに注目してください。ただし、分散の他の尺度はすべて劇的に変化します。
これは、四分位範囲が他の分散尺度と同様に外れ値の影響を受けないことを示しています。このため、任意の分布の中央の 50% の値の分布を測定できる信頼性の高い方法です。
参考文献:
分散測定
四分位範囲計算ツール