回帰直線
この記事では統計における回帰直線とは何かについて説明します。したがって、2 つの変数間の回帰直線を計算する方法、解決された演習、さらに、データのサンプルの回帰直線を計算するためのオンライン計算機を見つけることができます。
回帰直線とは何ですか?
統計学における回帰直線は、単純な線形回帰モデルから得られる直線です。より正確には、回帰直線は散布図に最もよく適合する直線であり、したがって一連の統計データを最もよく表します。
したがって、回帰直線方程式は、データセットの独立変数 X と従属変数 Y を数学的に関連付けます。回帰直線は通常、各観測値の値を正確に決定することはできませんが、その値の近似値を得ることができます。

前のグラフでわかるように、回帰直線は、データセットの傾向と、独立変数と従属変数の間にどのような種類の関係が存在するかを確認するのに役立ちます。以下では回帰直線の応用を見ていきます。
回帰直線の式
回帰直線の定義がわかったので、線形回帰モデルの直線の方程式を計算する方法を見てみましょう。
他の直線と同様、回帰直線の方程式は定数 (b 0 ) と傾き (b 1 ) で構成されます。
![]()
したがって、線形回帰直線の係数を計算する式は次のとおりです。
![Rendered by QuickLaTeX.com \begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[12ex]b_0=\overline{y}-b_1\overline{x}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-6dc6f56cacf0a233977c358d6a62fca8_l3.png)
金:
-
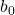
回帰直線の定数です。
-
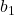
は回帰直線の傾きです。
-

データ i の独立変数 X の値です。
-

データ i の従属変数 Y の値です。
-

独立変数の値の平均です
-

従属変数 Y の値の平均です。
👉以下の計算機を使用して、任意のデータセットの回帰直線を計算できます。
回帰直線の具体例
回帰直線の概念をさらに詳しく調べるために、以下に回帰直線の作成方法の実例を示します。
- 統計試験を受けた後、5 人の学生が試験に費やした勉強時間について尋ねられました。データは以下の表に示されています。収集した統計データから回帰直線を計算し、学習時間と取得した成績を直線的に関連付けます。次に、8時間勉強した生徒が何級を受けるかを決定します。

サンプル データの回帰直線を見つけるには、方程式の係数 b 0と b 1を決定する必要があります。これを行うには、上のセクションで示した式を使用する必要があります。
ただし、線形回帰直線の式を適用するには、まず独立変数の平均と従属変数の平均を計算する必要があります。
![Rendered by QuickLaTeX.com \begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-7a7aa6f1f20fa4ff0d61a2ad0dd2ea1f_l3.png)
変数の平均がわかったので、対応する式を使用してモデルの係数 b 1を計算します。
![Rendered by QuickLaTeX.com \begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c9d90c766487cd7b6924e6b23d2d9c78_l3.png)
最後に、対応する式を使用してモデルの係数 b 0を計算します。
![Rendered by QuickLaTeX.com \begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c72e6b89a75681a88cf751ca39079240_l3.png)
つまり、問題の線形回帰直線の方程式は次のとおりです。
![]()
以下に、サンプル データのグラフ表現と単純な線形回帰モデルの直線を示します。

回帰直線を計算したら、8 時間勉強した生徒が取得する成績を予測するには、得られた回帰直線の方程式にこの値を代入するだけです。
![]()
したがって、実行された線形回帰モデルによると、学生が 8 時間勉強した場合、試験では 5.56 点を獲得します。
回帰直線は何に使用されますか?
主に、回帰直線には 2 つの用途があります。回帰直線は、2 つの変数間にどのようなタイプの関係が存在するかを判断するために使用されます。また、その一方で、回帰直線を使用すると、新しい観測値についての予測を行うこともできます。
回帰直線の傾きは、独立変数と従属変数の間の相関関係がどのようなものであるかを示します。傾きが正の場合、従属変数が独立変数に正比例することを意味し、傾きが負の場合、変数が反比例することを意味します。最後に、傾き係数がゼロに非常に近い場合、これは 2 つの変数間の相関が非常に弱いことを意味します。
さらに、回帰直線の方程式がわかっている場合は、上の例で行ったように、独立変数の新しい値について従属変数の値を予測できます。したがって、回帰直線が適切に適応されるほど、より適切な予測が行われます。
回帰直線計算ツール
次の計算機にデータのサンプルを入力して、2 つの変数間の回帰直線を計算します。最初のボックスには独立変数 X の値のみが含まれ、2 番目のボックスには従属変数 Y の値のみが含まれるように、データのペアを分離する必要があります。
データはスペースで区切られ、小数点としてピリオドを使用して入力する必要があります。