Mape 値の解釈方法
モデルの予測精度を測定するために最も一般的に使用されるメトリクスの 1 つは、平均絶対パーセント誤差( MAPEと略されることがよくあります) です。
次のように計算されます。
MAPE = (1/n) * Σ(|実際 – 予測| / |実際|) * 100
金:
- Σ – 「和」を意味する記号
- n – サンプルサイズ
- actual – データの実際の値
- 予測– データの予測値
MAPE は解釈が容易なため、一般的に使用されます。たとえば、MAPE 値 14% は、予測値と実際の値の平均差が 14% であることを意味します。
次の例は、特定のモデルの MAPE 値を計算して解釈する方法を示しています。
例: 特定のモデルの MAPE 値を解釈する
食料品チェーンが将来の売上を予測するモデルを構築しているとします。次のグラフは、12 連続の販売期間におけるモデルの実際の販売と予測販売を示しています。
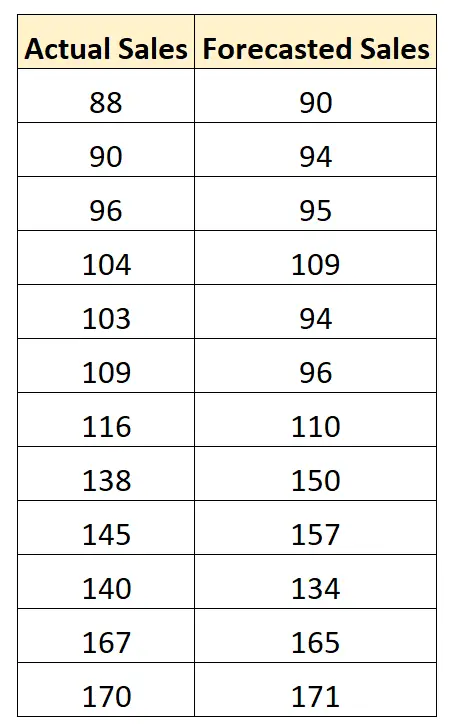
次の式を使用して、各予測の絶対誤差パーセンテージを計算できます。
- 絶対誤差パーセンテージ = |実際の予測| / |本物| *100
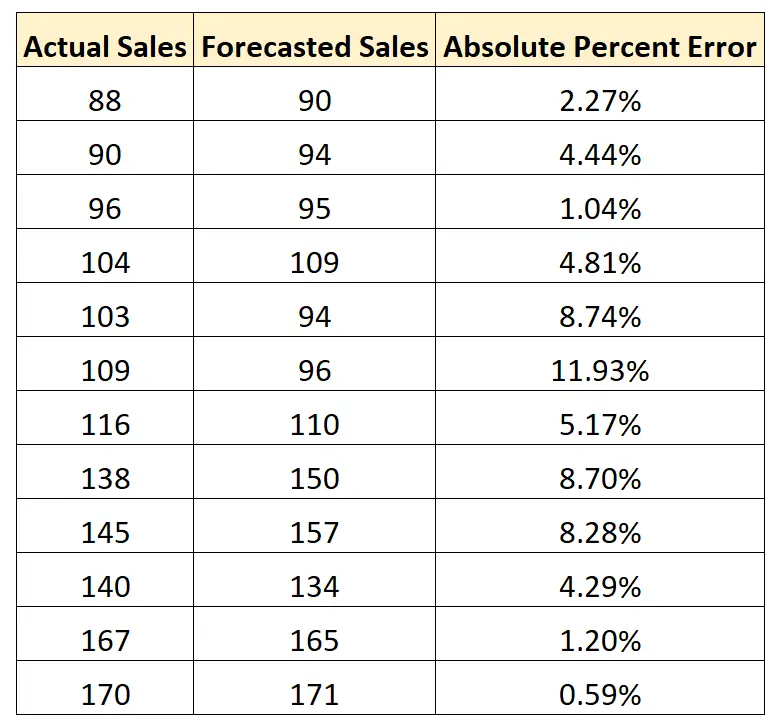
次に、絶対エラーのパーセンテージの平均を計算できます。
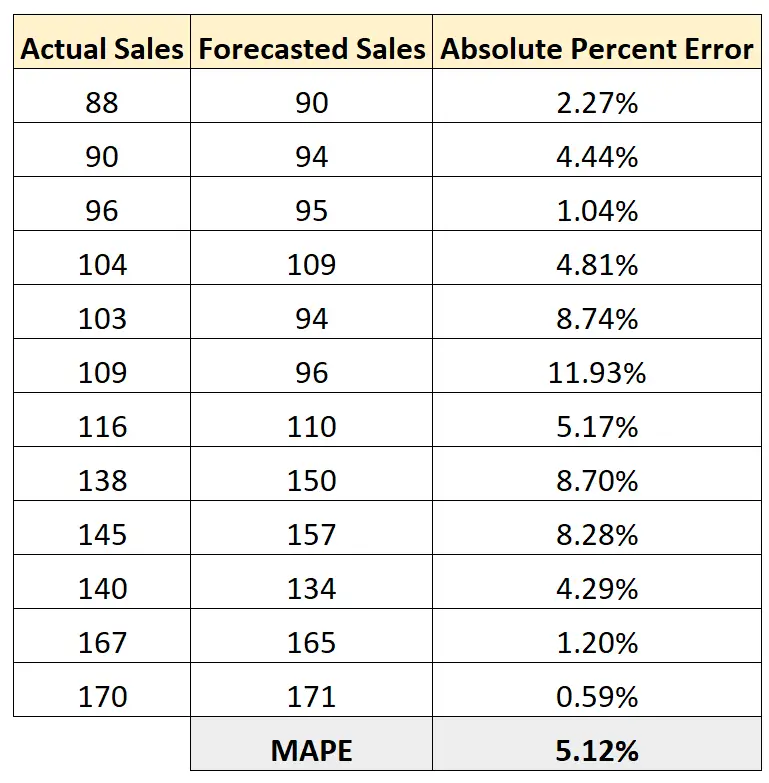
このモデルの MAPE は5.12%であることがわかります。
これは、モデル予測売上と実際の売上の間の平均絶対パーセント誤差が5.12%であることを示しています。
これがMAPE にとって適切な値であるかどうかは、業界標準によって決まります。
標準的な食品業界が生産するモデルの MAPE 値が 2% である場合、この値 5.12% は高いと考えられます。
逆に、ほとんどの業界の食料品予測モデルが 10% ~ 15% の MAPE 値を生成する場合、5.12% という MAPE 値は低いとみなされ、このモデルは将来の売上を予測するのに優れていると考えられます。
各種モデルのMAPE値の比較
MAPE は、さまざまなモデルの適合性を比較するのに特に役立ちます。
たとえば、食料品店チェーンが将来の売上を予測するモデルを作成し、いくつかの潜在的なモデルの中から可能な限り最良のモデルを見つけたいと考えているとします。
それらが 3 つの異なるモデルに一致し、対応する MAPE 値を見つけたとしましょう。
- モデル 1 の MAPE: 14.5%
- モデル 2 MAPE: 16.7%
- モデル 3 MAPE: 9.8%
モデル 3 は MAPE 値が最も低く、3 つの潜在的なモデルの中で最も高い精度で将来の売上を予測できることがわかります。
追加リソース
Excel で MAPE を計算する方法
RでMAPEを計算する方法
Python で MAPE を計算する方法
MAPE計算機