Stata の回帰で堅牢な標準誤差を使用する方法
重線形回帰は、複数の説明変数と応答変数の間の関係を理解するために使用できる方法です。
残念ながら、回帰でよく発生する問題は不均一分散として知られており、測定値の範囲にわたって残差の分散に系統的な変化が生じます。
これは回帰係数推定値の分散の増加につながりますが、回帰モデルではこれが考慮されていません。これにより、実際にはそうではないにもかかわらず、回帰モデルがモデル内の項が統計的に有意であると主張する可能性が非常に高くなります。
この問題を説明する 1 つの方法は、ロバストな標準誤差を使用することです。これは、不均一分散性の問題に対してより「ロバスト」であり、回帰係数の真の標準誤差のより正確な測定値を提供する傾向があります。
このチュートリアルでは、Stata の回帰分析で堅牢な標準誤差を使用する方法を説明します。
例: Stata の堅牢な標準誤差
自動的に統合された Stata データセットを使用して、回帰で堅牢な標準誤差を使用する方法を説明します。
ステップ 1: データをロードして表示します。
まず、次のコマンドを使用してデータをロードします。
システムの自動使用
次に、次のコマンドを使用して生データを表示します。
br
ステップ 2: 堅牢な標準誤差を使用せずに重回帰を実行します。
次に、次のコマンドを入力して、応答変数として価格、説明変数としてmpgとweightを使用して重線形回帰を実行します。
回帰価格 mpg 重量

ステップ 3: 堅牢な標準誤差を使用して重回帰を実行します。
次に、まったく同じ重線形回帰を実行しますが、今回は、Stata が堅牢な標準誤差の使用方法を認識できるようにvce(robust)コマンドを使用します。
回帰価格 mpg 重量、vce (ロバスト)
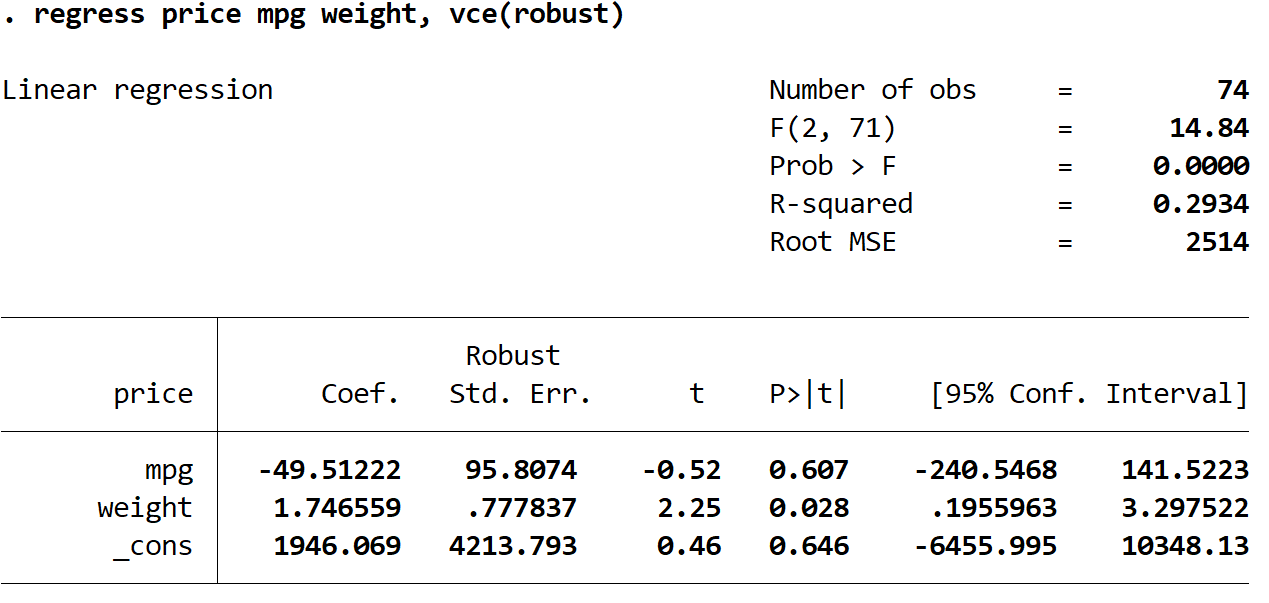
ここで注意すべき興味深い点がいくつかあります。
1. 係数推定値は同じままでした。ロバストな標準誤差を使用すると、係数推定値はまったく変化しません。 mpg、重量、および定数の係数推定値は、両方の回帰で次のようになります。
- mpg: -49.51222
- 重量: 1.746559
- _反対: 1946.069
2. 標準誤差が変更されました。ロバストな標準誤差を使用すると、各係数推定値の標準誤差が増加することに注意してください。
注:ほとんどの場合、ロバスト標準誤差は通常の標準誤差より大きくなりますが、まれに、ロバスト標準誤差が実際には小さくなる可能性があります。
3. 各係数の検定統計量が変更されました。各検定統計量tの絶対値が減少していることに注意してください。実際には、検定統計量は、推定係数を標準誤差で割ったものとして計算されます。したがって、標準誤差が大きいほど、検定統計量の絶対値は小さくなります。
4. p 値が変更されました。各変数の p 値も増加していることに注意してください。これは、検定統計量が小さいほど p 値が大きくなるからです。
係数の p 値は変更されましたが、 mpg変数は α = 0.05 で依然として統計的に有意ではなく、変数の重みは α = 0.05 で依然として統計的に有意です。