説明変数と応答変数: 定義と例
統計において理解すべき最も重要なタイプの変数の 2 つは、説明変数と応答変数です。
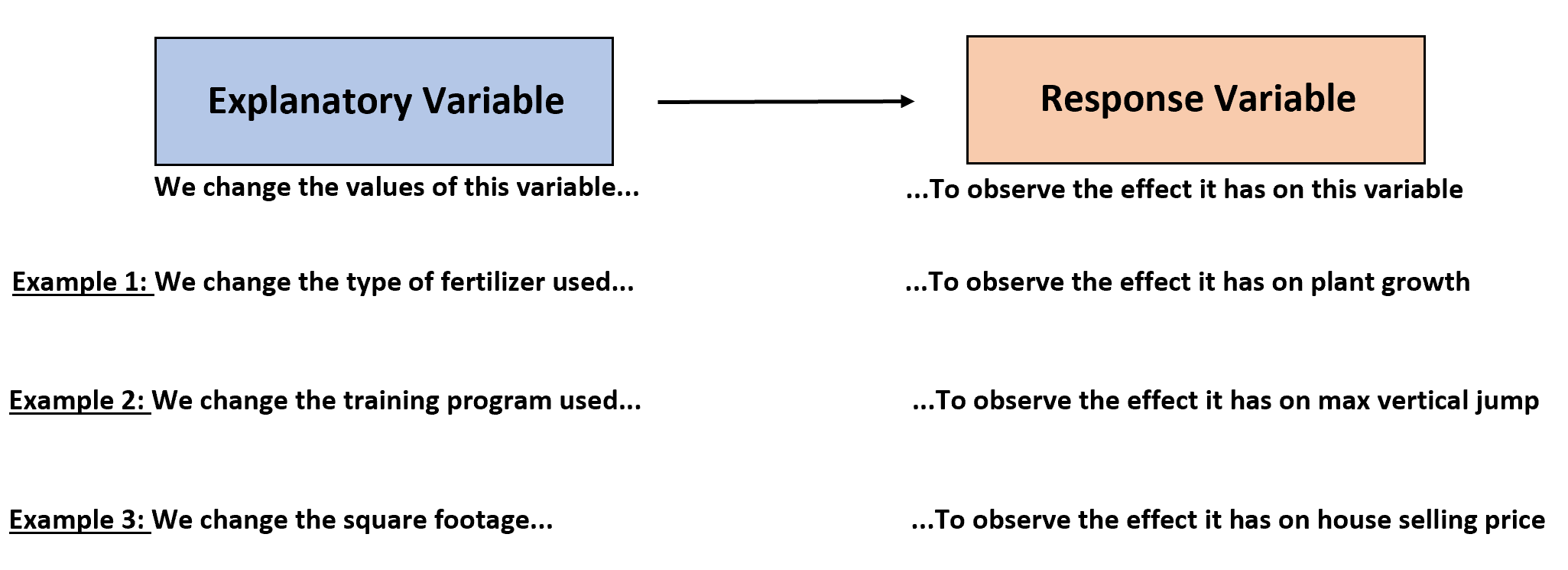
説明変数:独立変数または予測変数と呼ばれることもあり、この変数は応答変数の変動を説明します。
応答変数:従属変数または結果変数と呼ばれることもあります。この変数の値は説明変数の変化に応答します。
実験研究では、一般に、説明変数の値の変化によって応答変数の値がどのように変化するかに興味があります。
次の例は、説明変数と応答変数を含むさまざまなシナリオを示しています。
例 1: 植物の成長
植物学者は、植物の成長に対する 2 つの異なる肥料の効果を比較したいと考えています。彼女は畑からランダムに 20 本の植物を選択し、それらに肥料 A を 1 週間施用します。また、同じ畑から他の 20 株をランダムに選択し、それらに肥料 B を 1 週間施用します。 1 週間後、彼女は各グループの植物の平均成長を測定しました。
この例では、次のようになります。
説明変数:肥料の種類。これは、植物の成長に及ぼす影響を観察できるように変更する変数です。
応答変数:植物の成長。これは施肥量に応じて変化する変数です。
興味深い事実:この実験を実行するには2 サンプルの t 検定を使用します。
例 2: 最大垂直ジャンプ
バスケットボールのコーチは、選手の最大垂直ジャンプに対する 3 つの異なるトレーニング プログラムの効果を比較したいと考えています。 10 人のプレーヤーを 1 週間トレーニング プログラム A を使用するように、別の 10 人のプレーヤーを 1 週間トレーニング プログラム B を使用するように、別の 10 人のプレーヤーを 1 週間トレーニング プログラム C を使用するようにランダムに割り当てます。週の終わりに、各プレーヤーの最大垂直ジャンプを測定し、グループ間に大きな差があるかどうかを確認します。
この例では、次のようになります。
説明変数:使用されるトレーニング プログラムの種類。これは、最大垂直ジャンプに与える影響を観察できるように変更する変数です。
可変応答:最大垂直ジャンプ。これは、プレーヤーが使用するトレーニング プログラムに応じて変化する変数です。
興味深い事実:この実験を実行するには一元配置分散分析を使用します。
例 3: 不動産価格
不動産業者は、家の面積と販売価格の関係を理解したいと考えています。彼女は町内の 100 軒の住宅の面積と販売価格に関するデータを収集し、2 つの変数間の関係を分析します。
この例では、次のようになります。
説明変数:正方形の領域。これは、販売価格に与える影響を観察できるようにするために、その進化を観察する変数です。
応答変数:販売価格。家の面積の変化によって変化する変数です。
興味深い事実:この実験を実行するには単純な線形回帰を使用します。
まとめ
上記のそれぞれの例では、説明変数の値を変更し、その結果として生じる応答変数の値の変化を観察しました。
追加リソース
著者について
ベンジャミン・アンダーソン博士
私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。 統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る