Sas で外れ値を特定する方法 (例付き)

外れ値とは、データセット内の他の値から異常に離れている観測値です。外れ値は分析結果に影響を与える可能性があるため、問題となる場合があります。

データセット内の外れ値を特定する最も一般的な方法は、四分位範囲を使用することです。

四分位範囲 (IQR) は、データセット内の 75 パーセンタイル (Q3) と 25 パーセンタイル (Q1) の差です。値の平均 50% の分布を測定します。

通常、観測値が第 3 四分位 (Q3) より上の四分位範囲の 1.5 倍、または第 1 四分位 (Q1) より下の四分位範囲の 1.5 倍である場合、その観測値は外れ値として定義されます。

外れ値 = 観測値 > Q3 + 1.5*IQR または < Q1 – 1.5*IQR

次の例は、この式を使用して SAS のデータセット内の外れ値を特定する方法を示しています。

例: SAS での外れ値の特定

SAS に次のデータセットがあると仮定します。

 /*create dataset*/
data original_data;
    input team $points;
    datalines ;
At 18
B24
C26
D 34
E 38
F45
G 48
H 54
I 60
Day 73
K 79
L 85
M 94
No. 98
O 221
P 223
;
run ;

/*view dataset*/
proc print data = original_data;

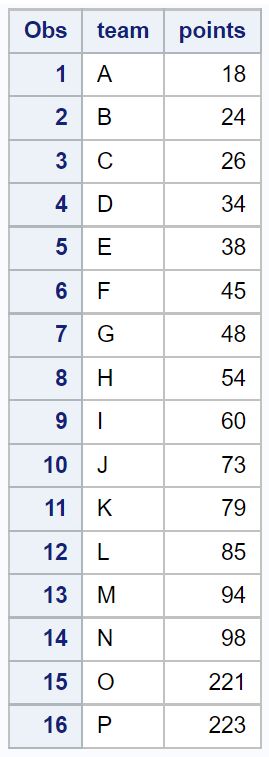
SAS で外れ値を特定する最も簡単な方法は、箱ひげ図を作成することです。これは、前述の式を自動的に使用して、データセット内の外れ値を特定し、小さな円として表示します。

 /*create boxplot to visualize distribution of points*/
ods output sgplot=boxplot_data;
proc sgplot data =original_data;
    vbox points;
run ;

/*view summary of boxplot descriptive statistics*/
proc print data =boxplot_data; 

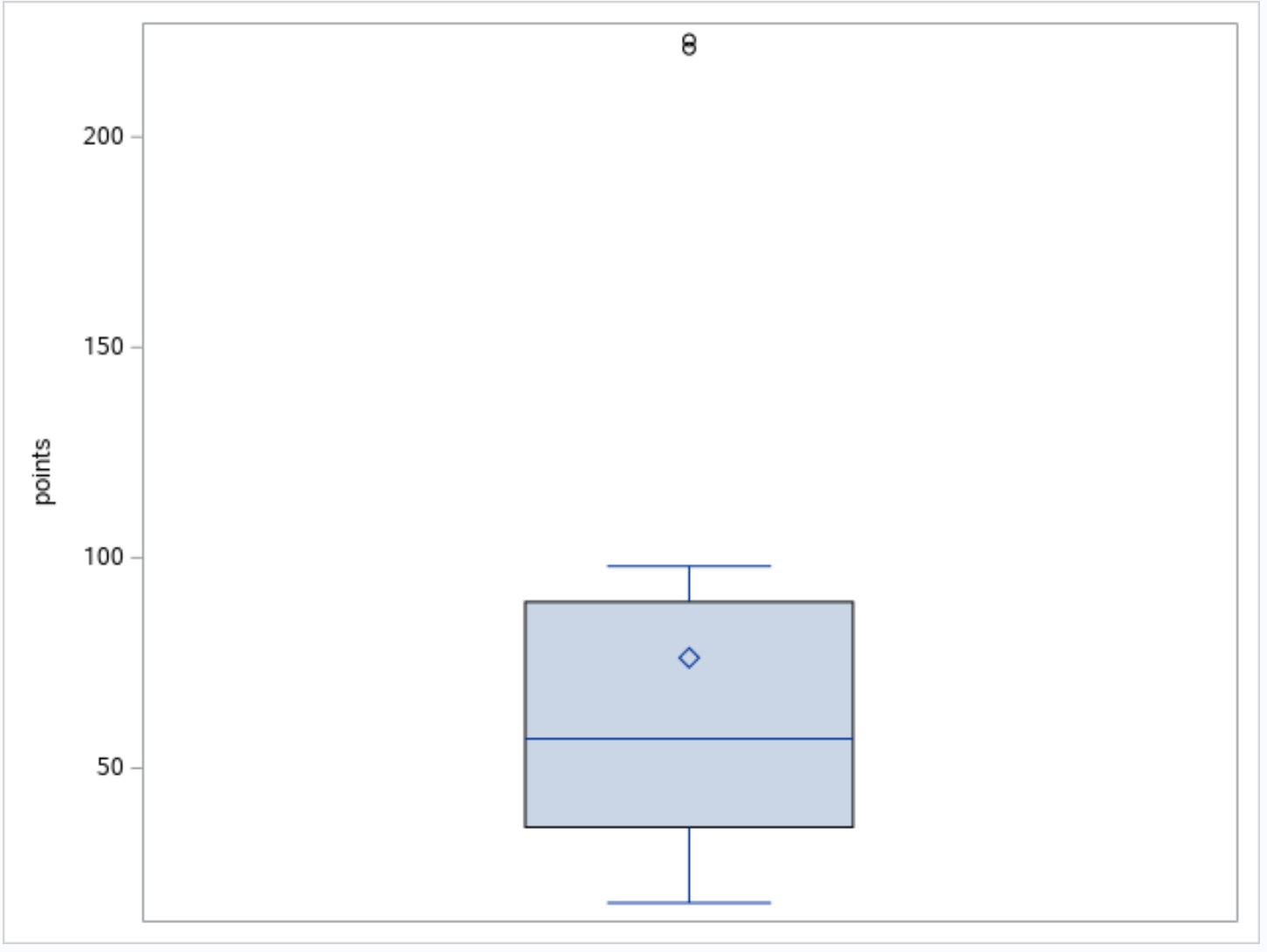
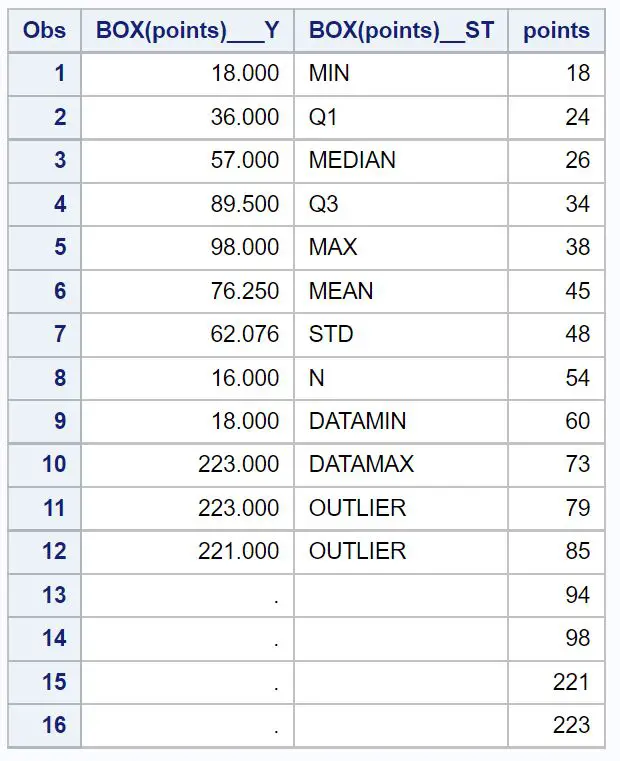
箱ひげ図から、プロットの上部近くに 2 つの小さな円があることがわかります。これは、外れ値が 2 つあることを示しています。

箱ひげ図の下の表では、2 つの外れ値221と223の正確な値がわかります。

前の式を使用して、これら 2 つの値が外れ値であることを手動で確認できます。

外れ値 = 観測値 > Q3 + 1.5*IQR または < Q1 – 1.5*IQR

四分位範囲は次のとおりです: Q3 – Q1 = 89.5 – 36 = 53.5。

外れ値の上限は、Q3 + 1.5*IQR = 89.5 + 1.5*53.5 = 169.75 となります。

221と223 は両方ともこの値より大きいため、外れ値として分類されます。

必要に応じて、次のコードを使用して、これら 2 つの外れ値をデータセットから削除できます。

 /*create new dataset with outliers removed*/
data new_data;
    set original_data;
    if points >= 221 then delete;
run ;

/*view new dataset*/
proc print data =new_data; 

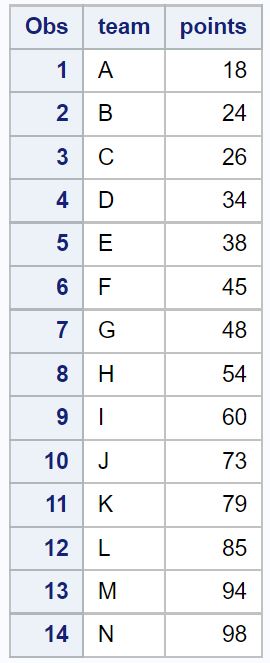
2 つの外れ値が削除されていることに注意してください。

追加リソース

次のチュートリアルでは、SAS で他の一般的なタスクを実行する方法について説明します。

SAS での手順の概要の使用方法
SAS で Proc Tabulate を使用する方法
SAS で相関関係を計算する方法
SAS で度数表を作成する方法
SAS で欠損値をゼロに置き換える方法