多項分布
この記事では、統計における多項分布とは何かについて説明します。したがって、多項分布の定義、その公式とは何か、解決された演習、およびこのタイプの確率分布の特性は何かがわかります。さらに、オンライン計算機を使用して多項分布の確率を計算できるようになります。
多項分布とは何ですか?
多項分布(または多項分布) は、いくつかの相互に排他的なイベントが数回の試行後に所定の回数発生する確率を記述する確率分布です。
つまり、ランダムな実験により 3 つ以上の排他的なイベントが発生する可能性があり、各イベントが個別に発生する確率がわかっている場合、多項分布を使用して、複数の実験が実行されたときに特定の数のイベントが発生する確率を計算します。毎回の時間。
したがって、多項分布は二項分布を一般化したものです。
多項分布式
多項分布確率を計算するには、まずデータの総数の階乗と各イベントの発生数の階乗の間の商を決定する必要があり、その結果に各イベントの確率の積を乗算します。当該事象の発生回数にもたらされる。
つまり、多項分布の公式は次のようになります。

金:
-
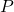
は、計算された多項分布の確率です。
-

実行されたテストの合計数です。
-

イベントが発生する回数です

。
-

出来事が起こる確率です

。
👉以下の計算機を使用して、多項分布に従う変数の確率を計算できます。
多項分布の例
多項分布の概念を理解するために、以下では多項分布の確率を計算する例を解決しました。
- ある店では 3 つの異なる製品が販売されています。顧客が購入する場合、それが製品 A、製品 B、製品 C である確率はそれぞれ 30%、15%、55% です。店舗が 8 個販売したときに、製品 A が 2 個、製品 B が 1 個、製品 C が 5 個になる確率を求めます。
定義された問題は多項分布によって支配されるため、このタイプの確率分布の公式を適用する必要があります。
![]()
そこで、問題のデータを式に代入して確率計算を実行します。
![]()
したがって、問題文に記載されていることが起こる確率は 11.4% です。
多項分布計算機
最初のボックスに各イベントの発生数を書き込み、2 番目のボックスに各イベントの発生確率を同じ順序で書き込みます。次に、最後の空白スペースに合計試行回数を入力します。
データはスペースで区切られ、小数点としてピリオドを使用して入力する必要があります。
多項分布の性質
多項分布には次の特徴があります。
- 多項分布では、 n回の試行を実行したときにイベントiが発生する回数の期待値は、実行された試行の総数にイベントが発生する確率を乗じたものに等しくなります。
![]()
- 多項分布では、イベントiの分散は次の式を使用して計算されます。
![]()
- 同様に、2 つのイベント間の共分散は、試行の総数と各イベントの確率を乗算し、-1 を乗算した積に相当します。
![]()
- 多項分布のモーメント生成関数は次のとおりです。