R の多項式回帰 (ステップバイステップ)
多項式回帰は、予測変数と応答変数の間の関係が非線形である場合に使用できる手法です。
このタイプの回帰は次の形式になります。
Y = β 0 + β 1 X + β 2 X 2 + … + β h
ここで、 hは多項式の「次数」です。
このチュートリアルでは、R で多項式回帰を実行する方法の段階的な例を示します。
ステップ 1: データを作成する
この例では、50 人の生徒のクラスの学習時間数と最終試験の成績を含むデータセットを作成します。
#make this example reproducible set.seed(1) #create dataset df <- data.frame(hours = runif (50, 5, 15), score=50) df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2) #view first six rows of data head(data) hours score 1 7.655087 64.30191 2 8.721239 70.65430 3 10.728534 73.66114 4 14.082078 86.14630 5 7.016819 59.81595 6 13.983897 83.60510
ステップ 2: データを視覚化する
回帰モデルをデータに当てはめる前に、まず散布図を作成して、学習時間と試験スコアの関係を視覚化しましょう。
library (ggplot2) ggplot(df, aes (x=hours, y=score)) + geom_point()
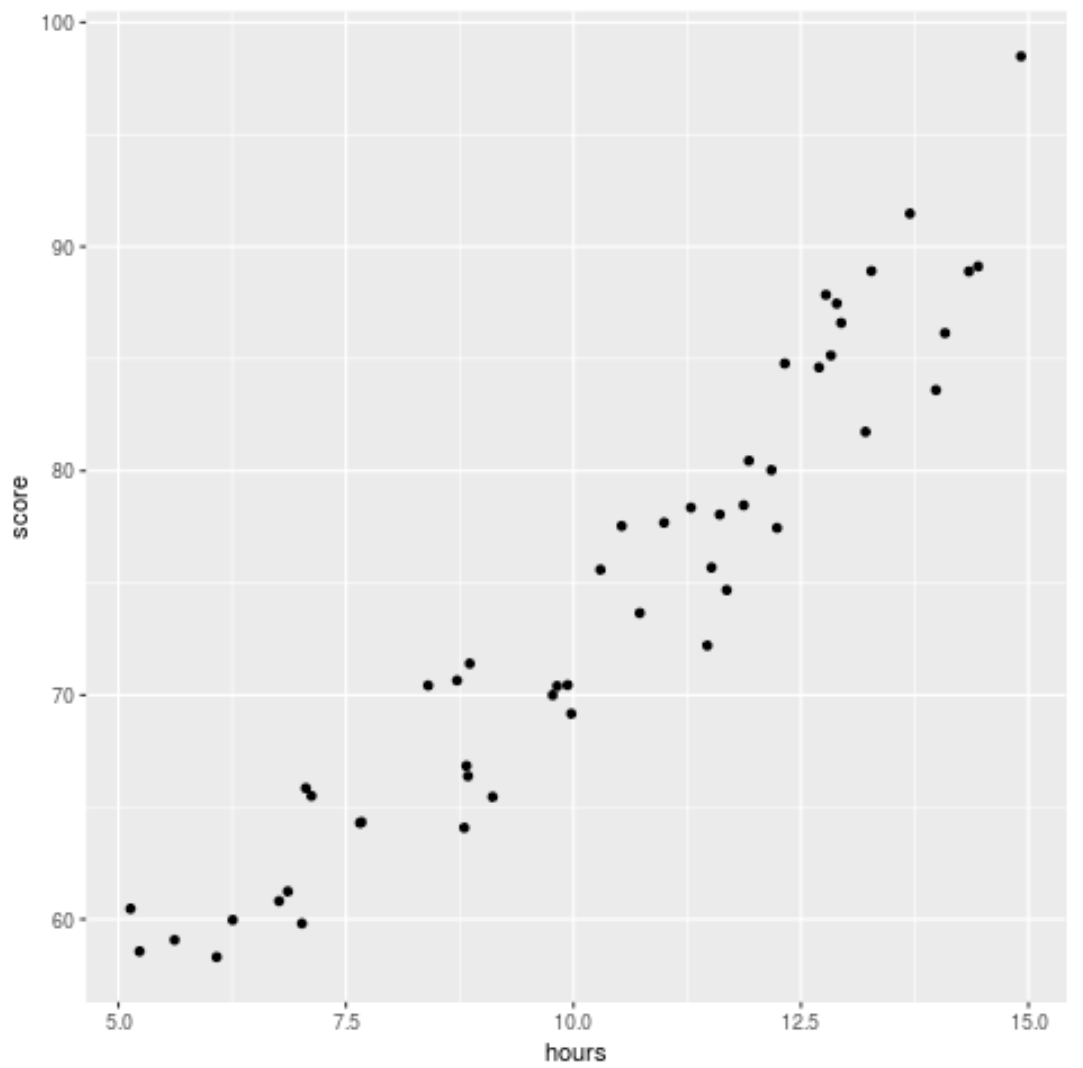
データにはわずかに 2 次の関係があることがわかり、単純な線形回帰よりも多項式回帰の方がデータによく適合する可能性があることを示しています。
ステップ 3: 多項式回帰モデルを当てはめる
次に、次数h = 1…5 で 5 つの異なる多項式回帰モデルを近似し、k = 10 回の k 分割相互検証を使用して各モデルの MSE 検定を計算します。
#randomly shuffle data
df.shuffled <- df[ sample ( nrow (df)),]
#define number of folds to use for k-fold cross-validation
K <- 10
#define degree of polynomials to fit
degree <- 5
#create k equal-sized folds
folds <- cut( seq (1, nrow (df.shuffled)), breaks=K, labels= FALSE )
#create object to hold MSE's of models
mse = matrix(data=NA,nrow=K,ncol=degree)
#Perform K-fold cross validation
for (i in 1:K){
#define training and testing data
testIndexes <- which (folds==i,arr.ind= TRUE )
testData <- df.shuffled[testIndexes, ]
trainData <- df.shuffled[-testIndexes, ]
#use k-fold cv to evaluate models
for (j in 1:degree){
fit.train = lm (score ~ poly (hours,d), data=trainData)
fit.test = predict (fit.train, newdata=testData)
mse[i,j] = mean ((fit.test-testData$score)^2)
}
}
#find MSE for each degree
colMeans(mse)
[1] 9.802397 8.748666 9.601865 10.592569 13.545547
結果から、各モデルの MSE テストがわかります。
- 次数 h = 1: 9.80の MSE テスト
- 次数 h = 2 の MSE テスト: 8.75
- 次数 h = 3 の MSE テスト: 9.60
- 次数 h = 4 の MSE テスト: 10.59
- 次数 h = 5 の MSE テスト: 13.55
テスト MSE が最も低いモデルは、次数h = 2 の多項式回帰モデルであることが判明しました。
これは、元の散布図からの直感と一致します。つまり、二次回帰モデルがデータに最もよく適合します。
ステップ 4: 最終モデルを分析する
最後に、最高のパフォーマンスを発揮するモデルの係数を取得できます。
#fit best model best = lm (score ~ poly (hours,2, raw= T ), data=df) #view summary of best model summary(best) Call: lm(formula = score ~ poly(hours, 2, raw = T), data = df) Residuals: Min 1Q Median 3Q Max -5.6589 -2.0770 -0.4599 2.5923 4.5122 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 54.00526 5.52855 9.768 6.78e-13 *** poly(hours, 2, raw = T)1 -0.07904 1.15413 -0.068 0.94569 poly(hours, 2, raw = T)2 0.18596 0.05724 3.249 0.00214 ** --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
結果から、最終的に適合されたモデルは次のとおりであることがわかります。
スコア = 54.00526 – 0.07904*(時間) + 0.18596*(時間) 2
この方程式を使用して、学習時間数に基づいて学生が受け取るスコアを推定できます。
たとえば、10 時間勉強した生徒の成績は71.81になるはずです。
スコア = 54.00526 – 0.07904*(10) + 0.18596*(10) 2 = 71.81
近似モデルをプロットして、生データにどの程度よく近似しているかを確認することもできます。
ggplot(df, aes (x=hours, y=score)) + geom_point() + stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + xlab(' Hours Studied ') + ylab(' Score ')
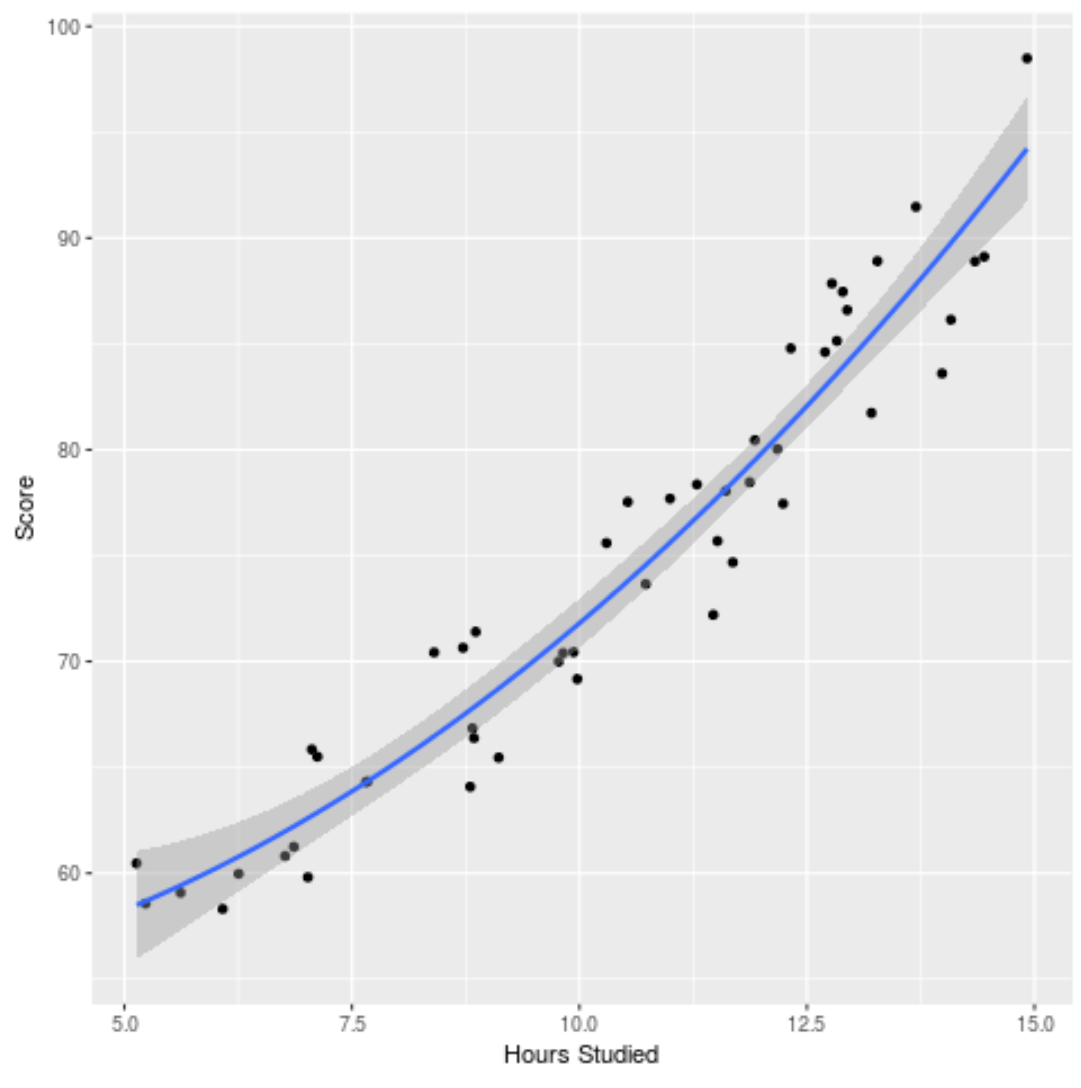
この例で使用されている完全な R コードは、 ここで見つけることができます。