Scikit-learn を使用して多項式回帰を実行する方法

多項式回帰は、予測変数と応答変数の間の関係が非線形である場合に使用できる手法です。

このタイプの回帰は次の形式になります。

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

ここで、 hは多項式の「次数」です。

次のステップバイステップの例は、sklearn を使用して Python で多項式回帰を実行する方法を示しています。

ステップ 1: データを作成する

まず、予測子と応答変数の値を保持する 2 つの NumPy 配列を作成しましょう。

 import matplotlib. pyplot as plt
import numpy as np

#define predictor and response variables
x = np. array ([2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12])
y = np. array ([18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29])

#create scatterplot to visualize relationship between x and y
plt. scatter (x,y)

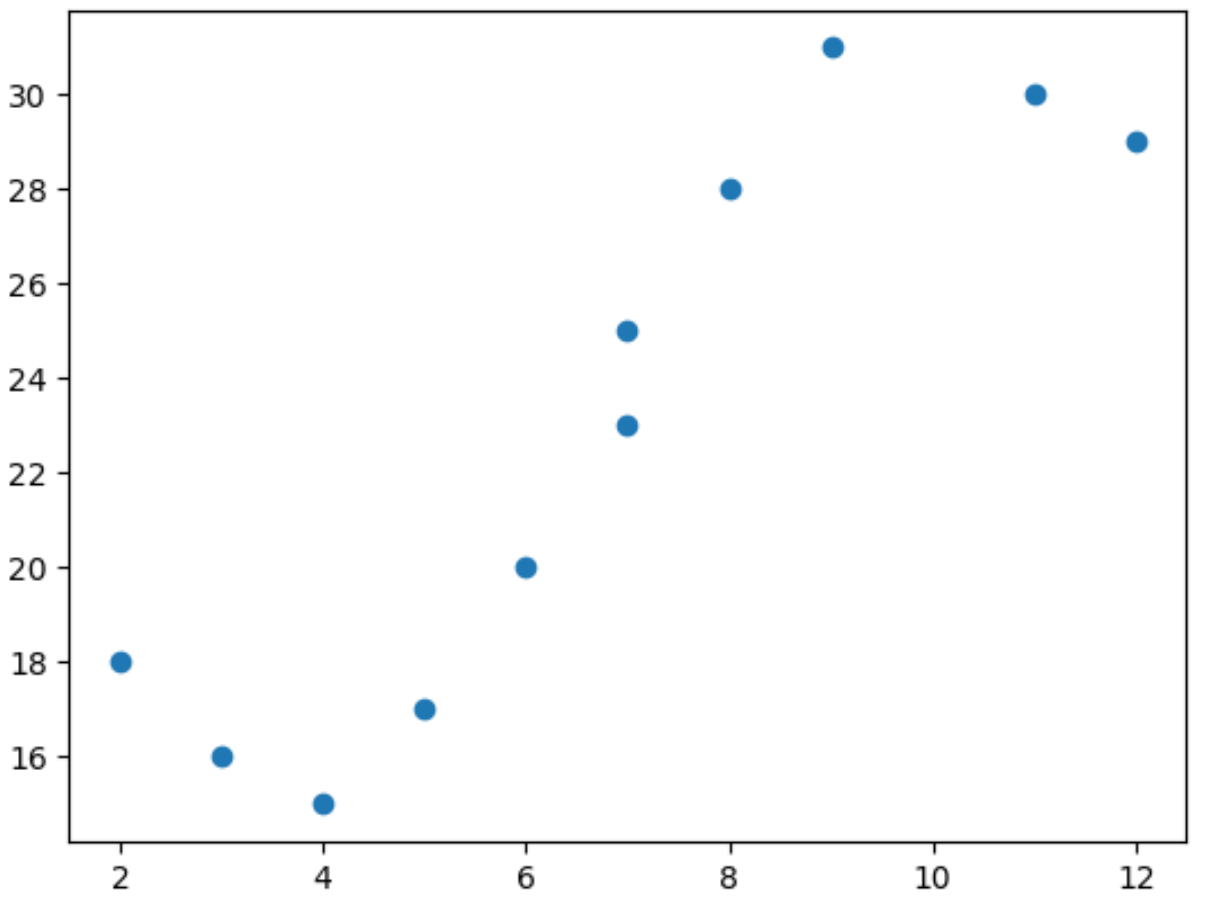
散布図から、x と y の関係が線形ではないことがわかります。

したがって、多項式回帰モデルをデータに当てはめて、2 つの変数間の非線形関係を把握することは良い考えです。

ステップ 2: 多項式回帰モデルを当てはめる

次のコードは、sklearn 関数を使用して、次数 3 の多項式回帰モデルをこのデータ セットに近似する方法を示しています。

 from sklearn. preprocessing import PolynomialFeatures
from sklearn. linear_model import LinearRegression

#specify degree of 3 for polynomial regression model
#include bias=False means don't force y-intercept to equal zero
poly = PolynomialFeatures(degree= 3 , include_bias= False )

#reshape data to work properly with sklearn
poly_features = poly. fit_transform ( x.reshape (-1, 1))

#fit polynomial regression model
poly_reg_model = LinearRegression()
poly_reg_model. fit (poly_features,y)

#display model coefficients
print (poly_reg_model. intercept_ , poly_reg_model. coef_ )

33.62640037532282 [-11.83877127 2.25592957 -0.10889554]

最後の行に示されているモデル係数を使用すると、次のように近似された多項式回帰方程式を書くことができます。

y = -0.109x ³ + 2.256x ² – 11.839x + 33.626

この方程式を使用すると、予測変数の特定の値が与えられた場合の応答変数の期待値を見つけることができます。

たとえば、x が 4 の場合、応答変数 y の期待値は 15.39 になります。

y = -0.109(4) ³ + 2.256(4) ² – 11.839(4) + 33.626= 15.39

注: 多項式回帰モデルを異なる次数で近似するには、 PolynomialFeature()関数の次数引数の値を変更するだけです。

ステップ 3: 多項式回帰モデルを視覚化する

最後に、元のデータ ポイントに適合した多項式回帰モデルを視覚化するための単純なプロットを作成できます。

 #use model to make predictions on response variable
y_predicted = poly_reg_model. predict (poly_features)

#create scatterplot of x vs. y
plt. scatter (x,y)

#add line to show fitted polynomial regression model
plt. plot (x,y_predicted,color=' purple ')

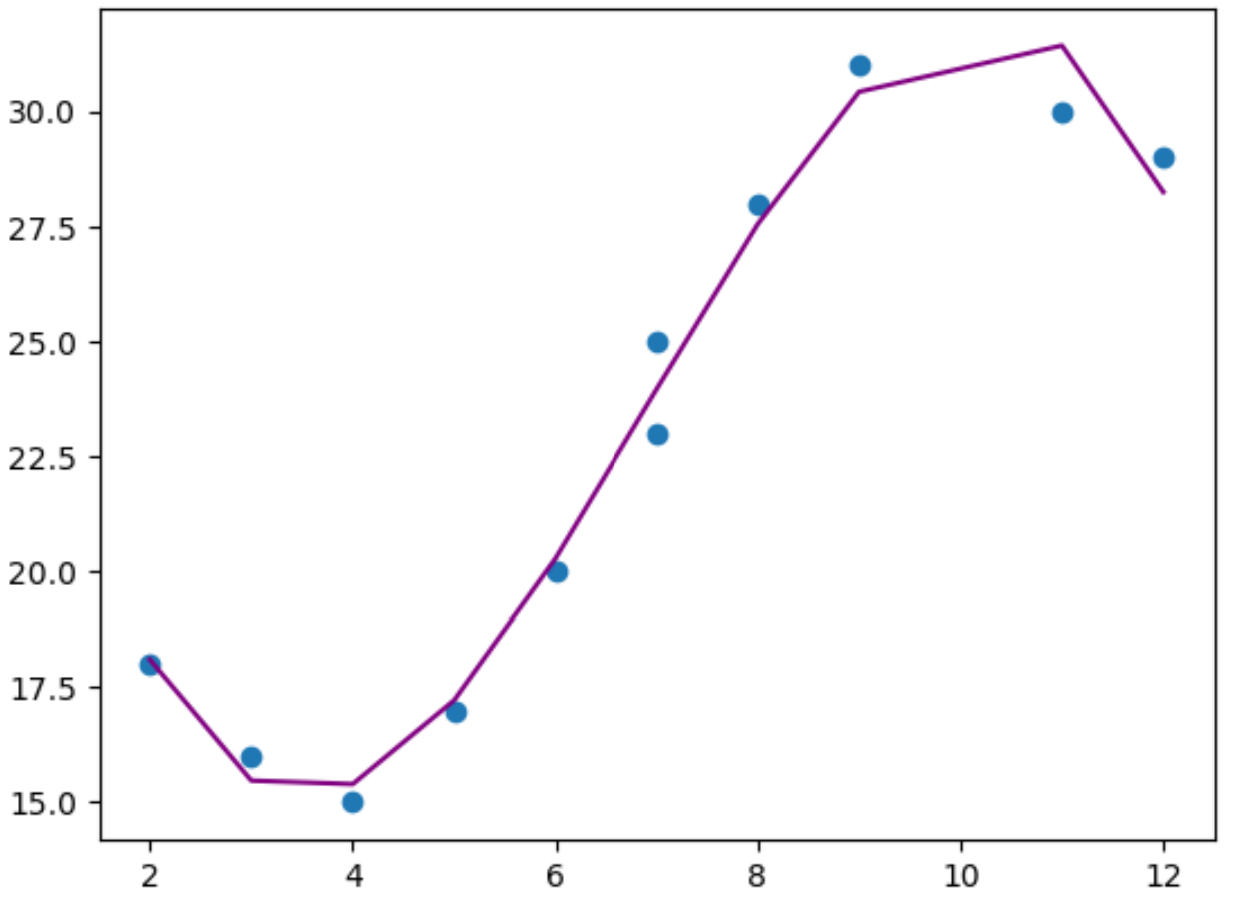
グラフから、多項式回帰モデルが過学習することなくデータによく適合していることがわかります。

注: sklearn PolynomialFeature()関数の完全なドキュメントはここで見つけることができます。

追加リソース

次のチュートリアルでは、sklearn を使用して他の一般的なタスクを実行する方法を説明します。

sklearnから回帰係数を抽出する方法
sklearn を使用してバランスのとれた精度を計算する方法
Sklearn で分類レポートを解釈する方法