Python で多項式回帰を実行する方法

回帰分析は、1 つ以上の説明変数と応答変数の間の関係を定量化するために使用されます。

最も一般的なタイプの回帰分析は単純線形回帰で、予測変数と応答変数が線形関係にある場合に使用されます。

ただし、予測変数と応答変数の間の関係が非線形になる場合があります。

たとえば、真の関係は二次関数である可能性があります。

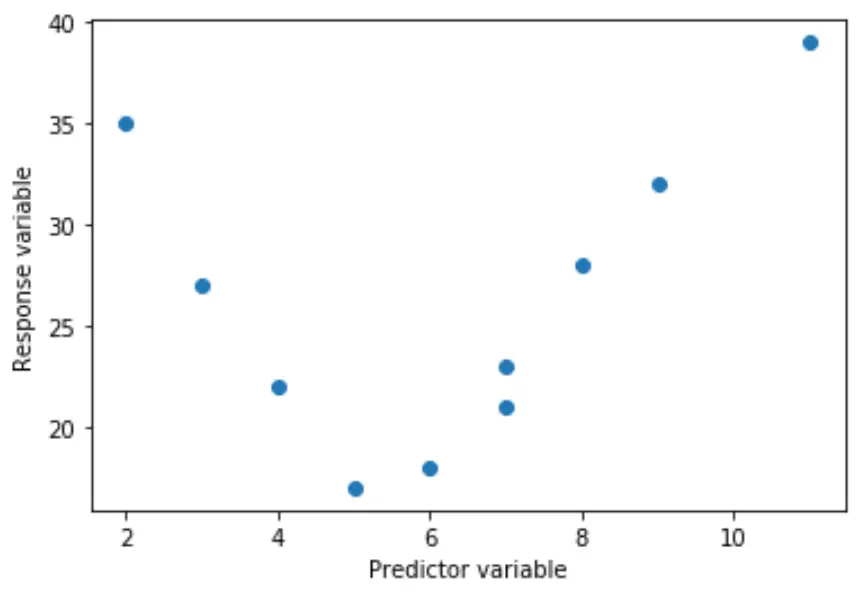
あるいは、次のような立方体にすることもできます。

このような場合、変数間の非線形関係を説明できる多項式回帰を使用することが合理的です。

このチュートリアルでは、Python で多項式回帰を実行する方法について説明します。

例: Python での多項式回帰

Python に次の予測変数 (x) と応答変数 (y) があるとします。

 x = [2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12]
y = [18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29]

このデータの単純な散布図を作成すると、x と y の関係が明らかに線形ではないことがわかります。

 import matplotlib.pyplot as plt

#create scatterplot 
plt.scatter(x, y)

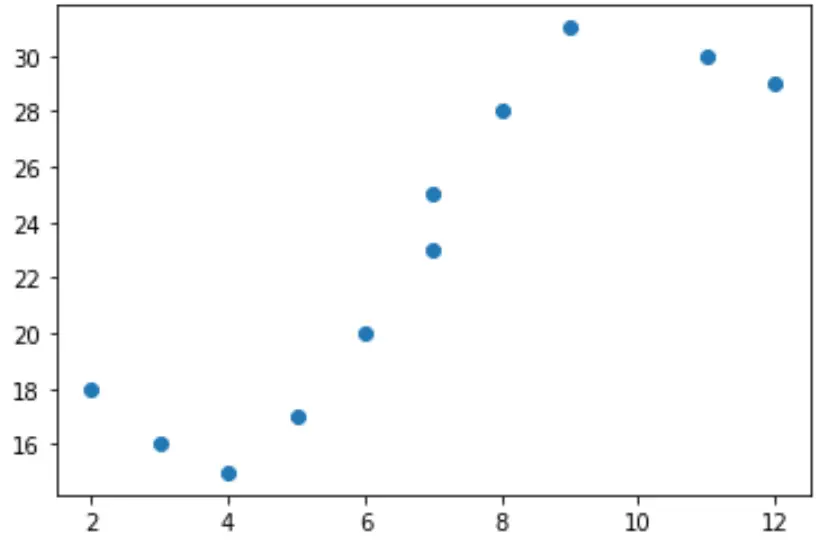
したがって、このデータに線形回帰モデルを当てはめることは意味がありません。代わりに、 numpy.polyfit()関数を使用して次数 3 の多項式回帰モデルの近似を試みることができます。

 import numpy as np

#polynomial fit with degree = 3
model = np.poly1d(np.polyfit(x, y, 3))

#add fitted polynomial line to scatterplot
polyline = np.linspace(1, 12, 50)
plt.scatter(x, y)
plt.plot(polyline, model(polyline))
plt.show() 

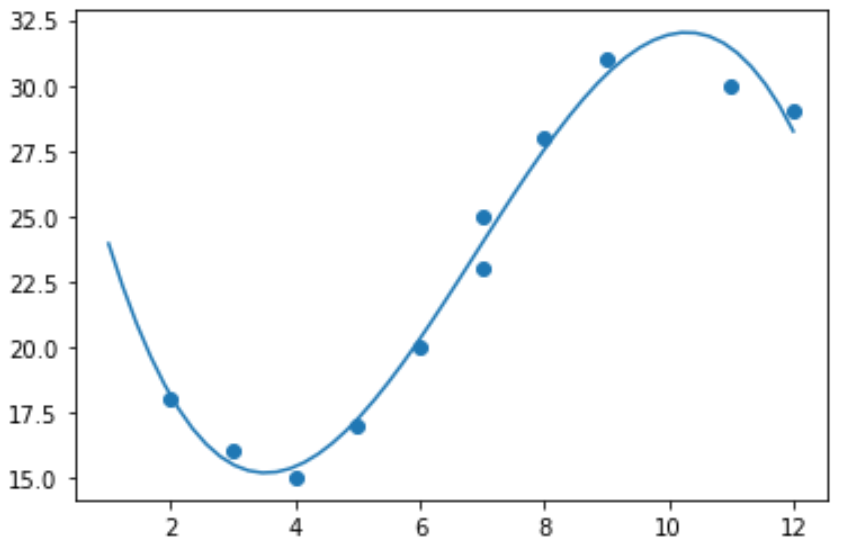
モデル係数を出力することで、近似された多項式回帰方程式を取得できます。

 print(model)

poly1d([ -0.10889554, 2.25592957, -11.83877127, 33.62640038])

近似された多項式回帰式は次のとおりです。

y = -0.109x ³ + 2.256x ² – 11.839x + 33.626

この方程式を使用すると、説明変数の特定の値が与えられた場合の応答変数の期待値を見つけることができます。

たとえば、x = 4 と仮定します。応答変数 y の期待値は次のようになります。

y = -0.109(4) ³ + 2.256(4) ² – 11.839(4) + 33.626= 15.39 。

モデルの R 二乗 (予測子変数によって説明できる応答変数の分散の割合) を取得する短い関数を作成することもできます。

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = numpy.polyfit(x, y, degree)
    p = numpy.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = numpy.sum(y)/len(y)
    ssreg = numpy.sum((yhat-ybar)**2)
    sstot = numpy.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(x, y, 3)

{'r_squared': 0.9841113454245183}

この例では、モデルの R 二乗は0.9841です。

これは、応答変数の変動の98.41%が予測変数によって説明できることを意味します。