多項式回帰を使用する必要があるのはどのような場合ですか?
多項式回帰は、予測変数と応答変数の間の関係が非線形である場合に、回帰モデルを近似するために使用できる手法です。
多項式回帰モデルは次の形式になります。
Y = β 0 + β 1 X + β 2 X 2 + … + β h
実際には、多項式回帰と線形回帰のような単純なモデルのどちらを使用するかを判断する簡単な方法が 3 つあります。
1. 予測変数と応答変数の散布図を作成します。
多項式回帰を使用する必要があるかどうかを判断する最も簡単な方法は、予測変数と応答変数の単純な散布図を作成することです。
たとえば、予測変数「学習時間」を使用して、学生が期末試験で受け取るであろう成績を予測したいとします。
回帰モデルを当てはめる前に、まず試験結果に対する学習時間の散布図を作成できます。散布図が次のようになっているとします。
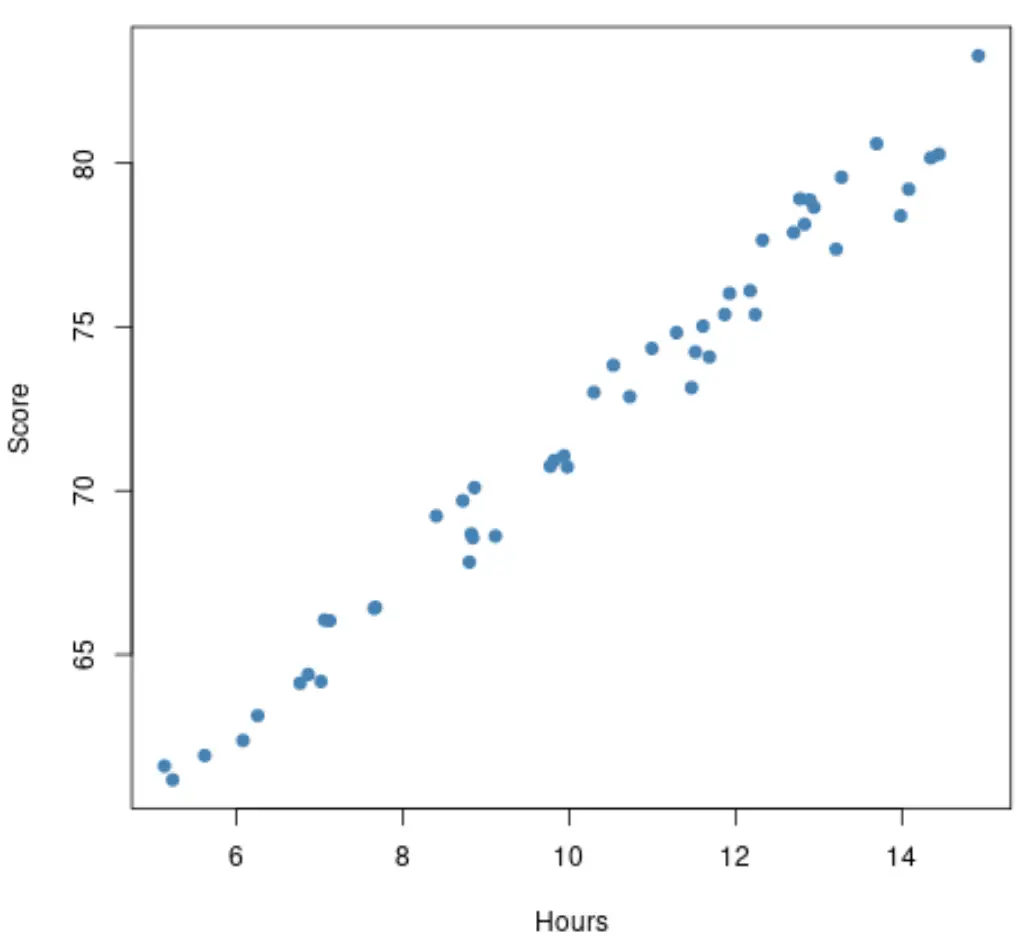
学習時間と試験結果の関係は線形であるため、このデータセットに単純な線形回帰モデルを当てはめることは理にかなっています。
ただし、散布図が実際には次のようになっていると仮定します。
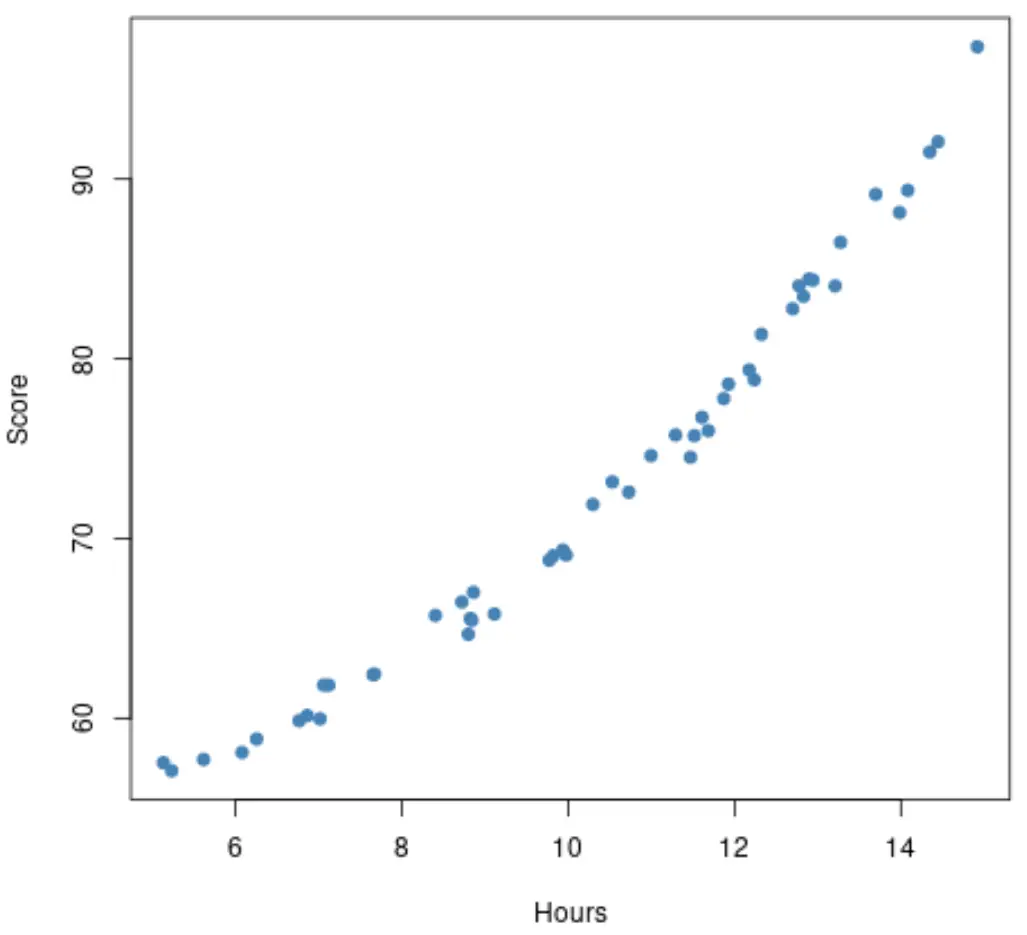
この関係はもう少し非線形であるように見えます。これは、代わりに多項式回帰モデルを当てはめることが賢明である可能性があることを示しています。
2. 近似値と残差値のグラフを作成する
多項式回帰を使用する必要があるかどうかを判断する別の方法は、線形回帰モデルをデータセットに近似し、モデルの残差に対する近似値のプロットを作成することです。
残差に明らかな非線形傾向がある場合、多項式回帰の方がデータによりよく適合する可能性があることを示しています。
たとえば、学習時間を予測変数として、試験のスコアを応答変数として使用して線形回帰モデルを近似し、残差に対する近似値の次のプロットを作成するとします。
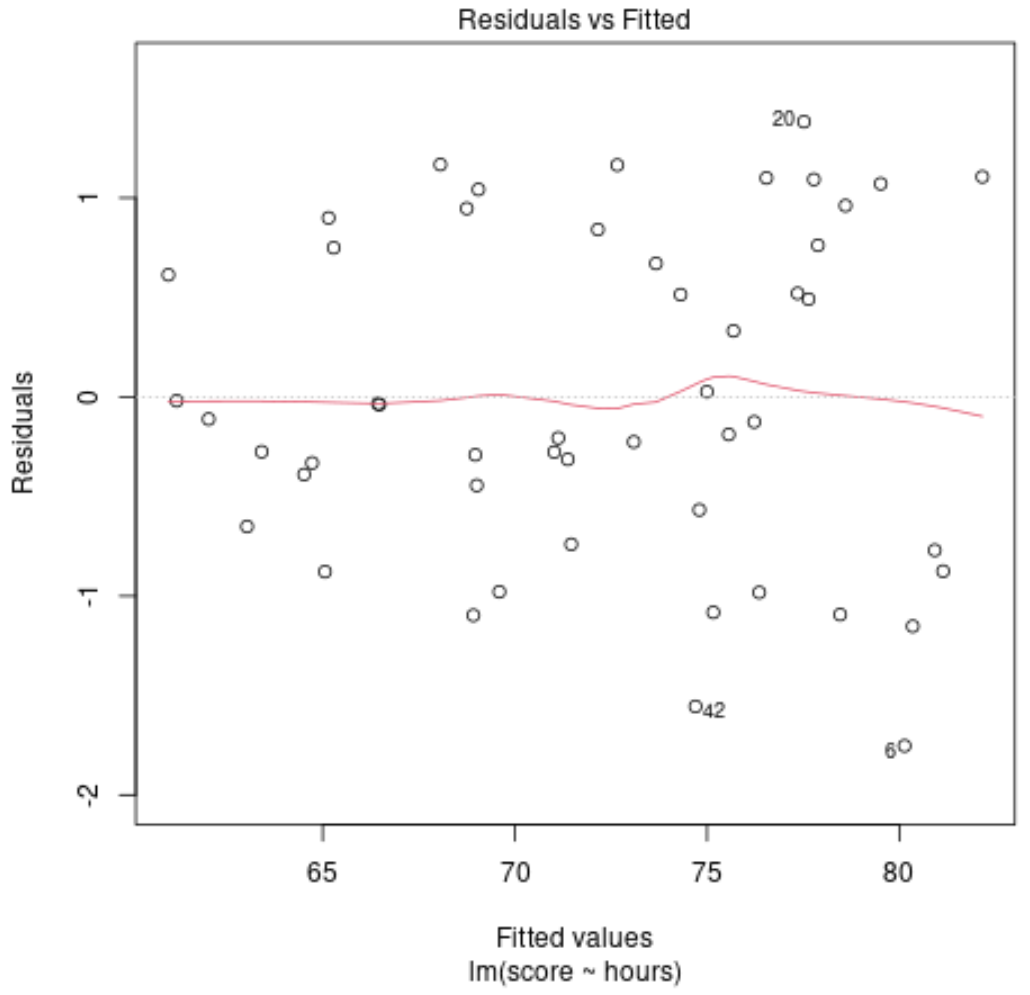
残差はゼロの周囲にランダムに散在しており、明確なパターンはありません。これは、線形モデルがデータに適切に適合していることを示しています。
ただし、近似値と残差のプロットが実際には次のようになっていると仮定します。
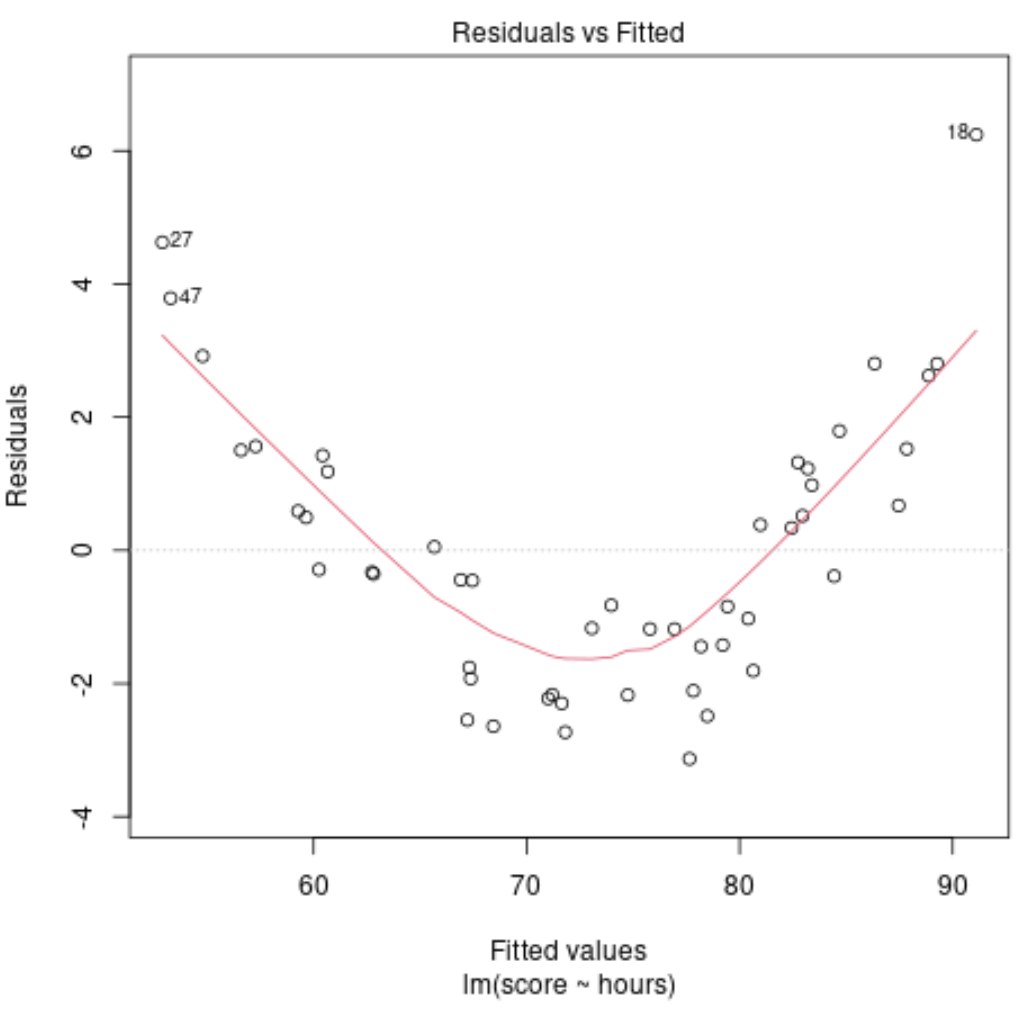
グラフから、残差に明確な非線形パターンがあることがわかります。残差は「U」字型を示しています。
これは、線形モデルがこの特定のデータには適切ではなく、代わりに多項式回帰モデルを近似することが賢明である可能性があることを示しています。
3. モデルの調整された R 二乗値を計算します。
多項式回帰を使用する必要があるかどうかを判断するもう 1 つの方法は、線形回帰モデルと多項式回帰モデルの両方を近似し、両方のモデルの近似 R 二乗値を計算することです。
調整済み R 二乗は、モデル内の予測子変数の数で調整された、モデル内の予測子変数によって説明できる応答変数の分散の割合を表します。
調整された R 二乗が最も高いモデルは、応答変数の変動を説明するために予測子変数を最もよく使用できるモデルを表します。
追加リソース
次のチュートリアルでは、さまざまな統計ソフトウェアを使用して多項式回帰を実行する方法について説明します。
多項式回帰の概要
R で多項式回帰を実行する方法
Python で多項式回帰を実行する方法
Excel で多項式回帰を実行する方法