多項検定とは何ですか? (定義&例)
多項検定は、カテゴリ変数が仮説分布に従うかどうかを判断するために使用されます。
この検定では、次の帰無仮説と対立仮説を使用します。
H 0 :カテゴリ変数は仮説分布に従います。
H A :カテゴリ変数は仮説の分布に従いません。
検定のp 値が特定の有意水準 (例: α = 0.05) を下回っている場合、帰無仮説を棄却し、変数が仮説の分布に従っていないと結論付けることができます。
このテストは、変数がk 個の異なる結果を取得できる場合に使用されます。多項テストの典型的な例は、特定のサイコロが公平かどうかを判断する場合です。サイコロを振ったとき、各数字(1 ~ 6)に当たる確率は 1/6 です。
サイコロが公平かどうかをテストするには、何度もサイコロを振って、異なる数字が出た回数が予想と大幅に異なるかどうかを確認します。
次の例は、R 統計プログラミング言語を使用して多項検定を実行する方法を示しています。
例 1: フェアダイス
サイコロが公平かどうかを判断したいとします。これをテストするために、30 回実行し、各結果の頻度を記録します。次の表に結果を示します。
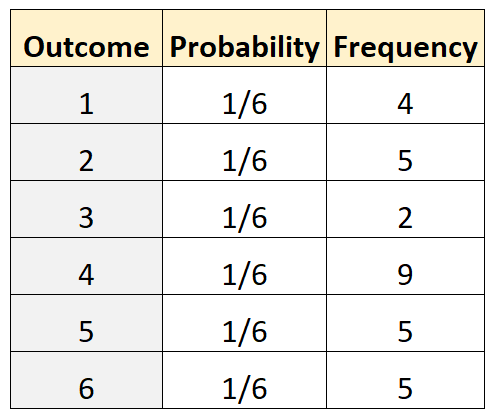
R の次のコードを使用して、多項検定を実行できます。
library (EMT)
#specify probability of each outcome
prob <- c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6)
#specify frequency of each outcome from experiment
actual <- c(4, 5, 2, 9, 5, 5)
#perform multinomial test
multinomial. test (actual, prob)
Exact Multinomial Test, distance measure: p
Events pObs p.value
324632 0 0.4306
検定の p 値は0.4306です。この p 値は 0.05 未満ではないため、帰無仮説は棄却されません。したがって、サイコロが不公平であると言える十分な証拠はありません。
例2:物販
店主が、同数の顧客が 4 つの異なる製品をそれぞれ購入すると仮定するとします。これをテストするために、特定の週に各製品を購入した顧客の数を記録します。次の表に結果を示します。
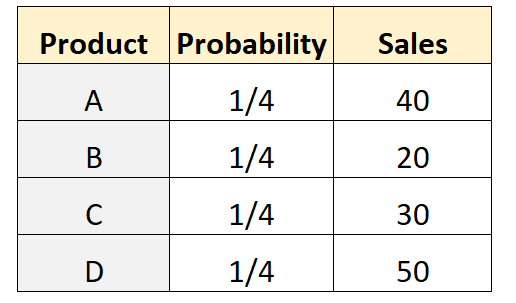
R の次のコードを使用して、このデータセットに対して多項検定を実行できます。
library (EMT)
#specify probability of each outcome
prob <- c(1/4, 1/4, 1/4, 1/4)
#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)
#perform multinomial test
multinomial. test (actual, prob)
Exact Multinomial Test, distance measure: p
Events pObs p.value
477191 0 0.00226
検定の p 値は0.00226です。この p 値は 0.05 未満であるため、帰無仮説を棄却します。したがって、各製品の売上が均等ではないことを示す十分な証拠があります。
例 3: 袋の中のビー玉
トムは、袋から赤、緑、紫のビー玉を選ぶ確率はそれぞれ 0.2、0.5、0.3 であると述べています。これをテストするために、彼の友人のマイクはバッグに手を入れてビー玉 (代替品あり) を 100 回取り出しました。次の表に結果を示します。
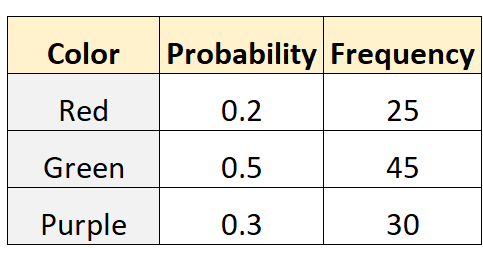
R の次のコードを使用して、このデータセットに対して多項検定を実行できます。
library (EMT)
#specify probability of each outcome
prob <- c(.2, .5, .3)
#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)
#perform multinomial test
multinomial. test (actual, prob)
Exact Multinomial Test, distance measure: p
Events pObs p.value
5151 0.0037 0.3999
検定の p 値は0.3999です。この p 値は 0.05 未満ではないため、帰無仮説を棄却できません。したがって、バッグ内のビー玉の分布がトムが指定したものと異なると言える十分な証拠がありません。