対応のある t 検定で定式化された 3 つの仮説
対のあるサンプルの t 検定は、一方のサンプルの各観測値がもう一方のサンプルの観測値と関連付けられる場合に、2 つのサンプルの平均を比較するために使用されます。
このタイプのテストでは、データに関して次の仮定が行われます。
1. 独立性:各観測値は他の観測値から独立している必要があります。
2. 正規性:ペア間の差異はほぼ正規分布する必要があります。
3. 極端な外れ値がない:差に極端な外れ値があってはなりません。
これらの仮定の 1 つ以上が満たされない場合、対応のあるサンプルの t 検定の結果は信頼性がないか、誤解を招く可能性があります。
このチュートリアルでは、各前提の説明、前提が満たされているかどうかを判断する方法、および前提に違反している場合の対処方法について説明します。
仮説 1: 独立性
対応のあるサンプルの t 検定では、各観測値が他のすべての観測値から独立していると仮定します。
この仮説を検証する方法
この仮定を検証する最も簡単な方法は、各観測値が ランダム サンプリング法を使用して収集されたことを検証することです。
ランダムなサンプリング方法 (単純なランダム サンプリングなど) が使用された場合、各観測値は他のすべての観測値から独立していると想定できます。
この前提が尊重されない場合はどうすればよいか
この仮定が満たされない場合、対応のあるサンプルの t 検定の結果は完全に無効になります。
このシナリオでは、各観測値が独立していることを保証するために、ランダム サンプリング方法を使用して新しい観測値を収集することが最善です。
仮説 2: 正常性
ペアのあるサンプルの t 検定は、ペア間の差がほぼ正規分布することを前提としています。
ペア間の差異が正規分布していない場合、結論を引き出すために検定の p 値を使用することは無効であるため、これは重要な仮定です。
この仮説を検証する方法
この仮説をテストする最も簡単な方法は、ペアになった差分のヒストグラムを作成し、ヒストグラムが釣鐘型かどうかを視覚的に確認することです。
たとえば、ヒストグラムが次のようであれば、正規性の仮定が満たされていると言えます。
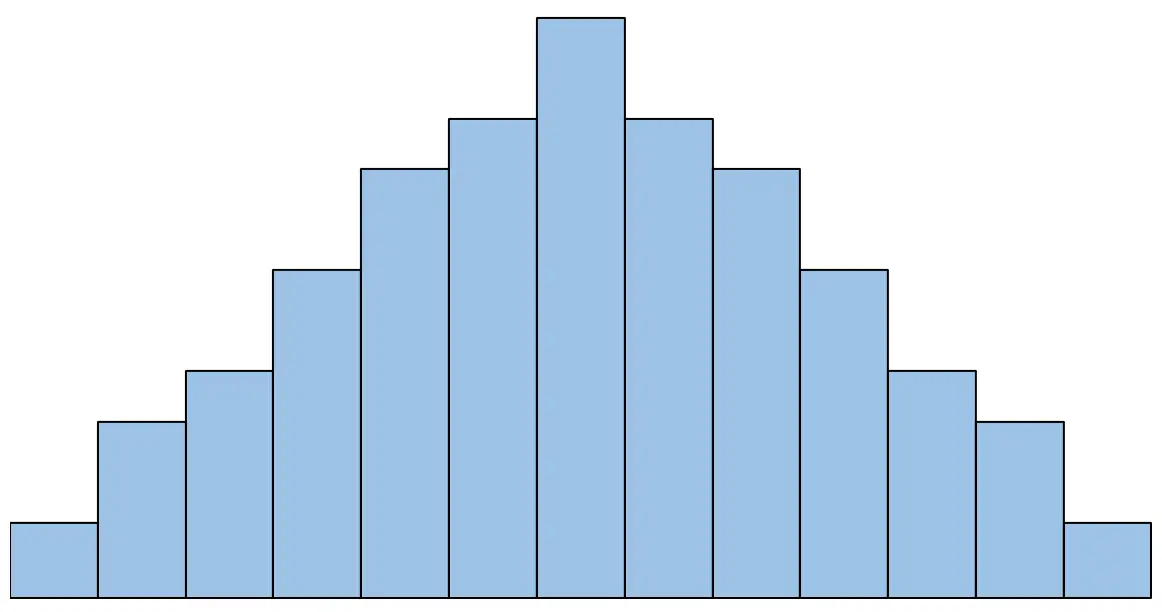
ただし、ヒストグラムが次のようになった場合は、正規性の仮定が満たされていないと言えます。
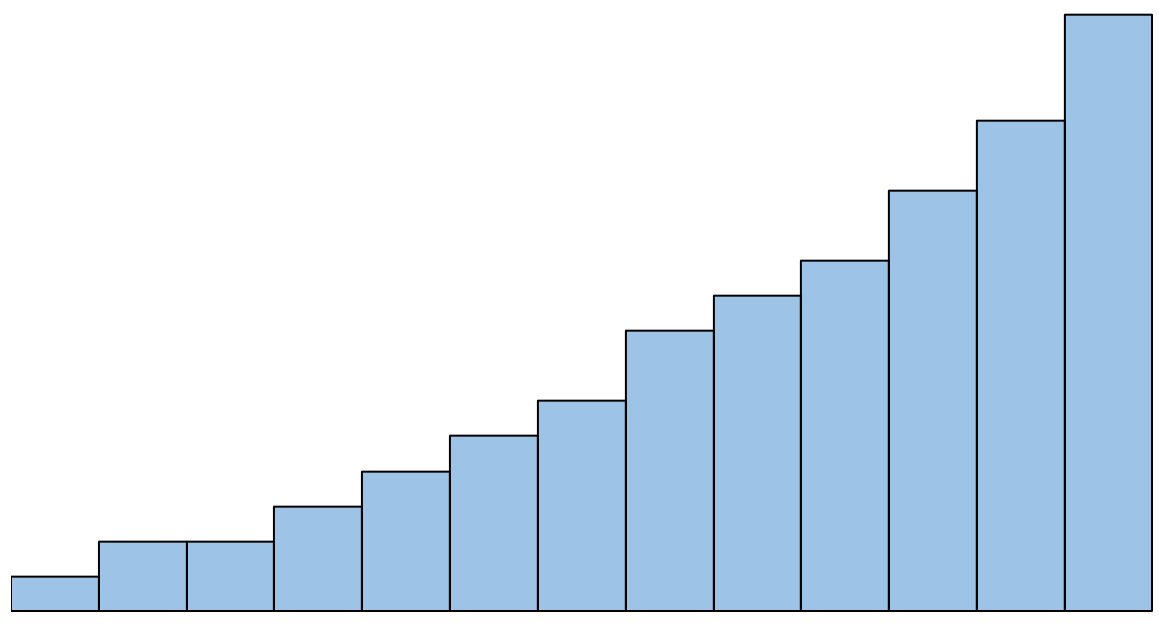
この前提が尊重されない場合はどうすればよいか
この仮定に違反する場合は、 ウィルコクソンの符号付き順位検定を実行できます。これは、ペアのサンプルの t 検定とノンパラメトリックな等価とみなされ、ペアの差が正規分布しているとは想定されません。
仮説 3: 極端な外れ値は存在しない
対応のあるサンプルの t 検定は、データに極端な外れ値が存在しないことを前提としています。
この仮説を検証する方法
この仮説をテストする最も簡単な方法は、一対の差の箱ひげ図を作成し、外れ値があるかどうかを視覚的に確認することです。
たとえば、一対の差の箱ひげ図が次のようになっているとします。
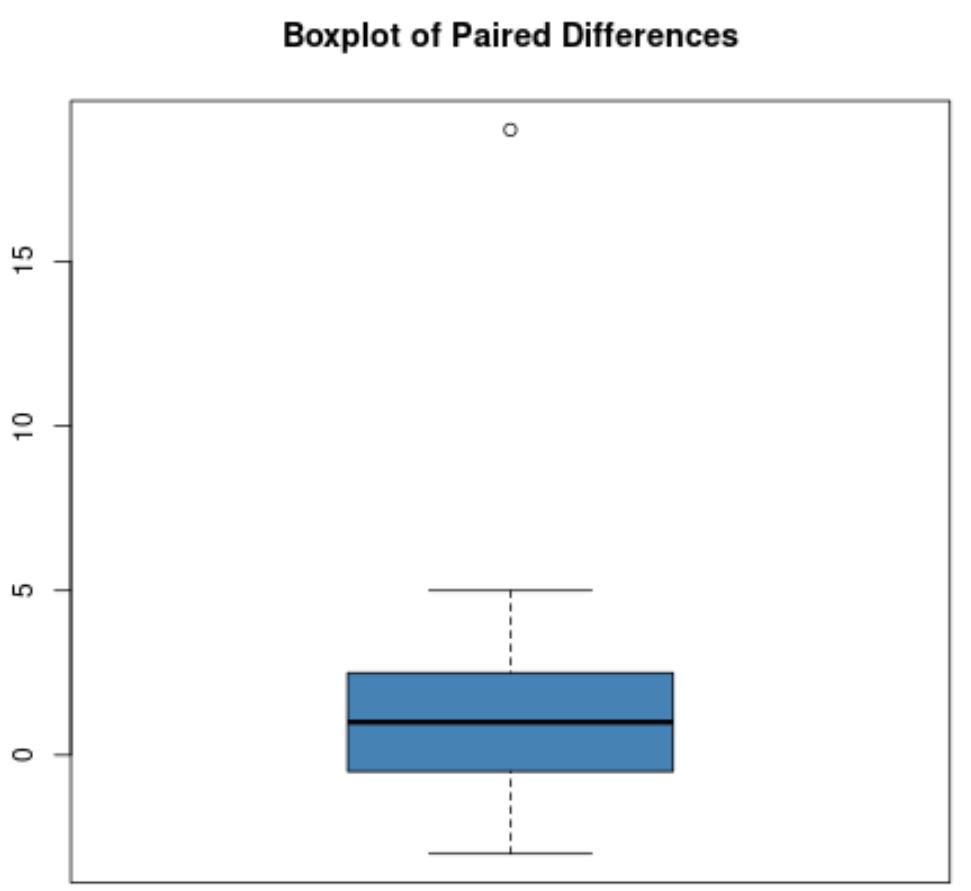
ほとんどのペアの差はゼロに近いですが、約 19 に等しいペアの差が 1 つあり、これは明らかに外れ値です。
注: 円は通常、外れ値を示すために箱ひげ図で使用されます。
ただし、一対の差の箱ひげ図が次のようになっているとします。
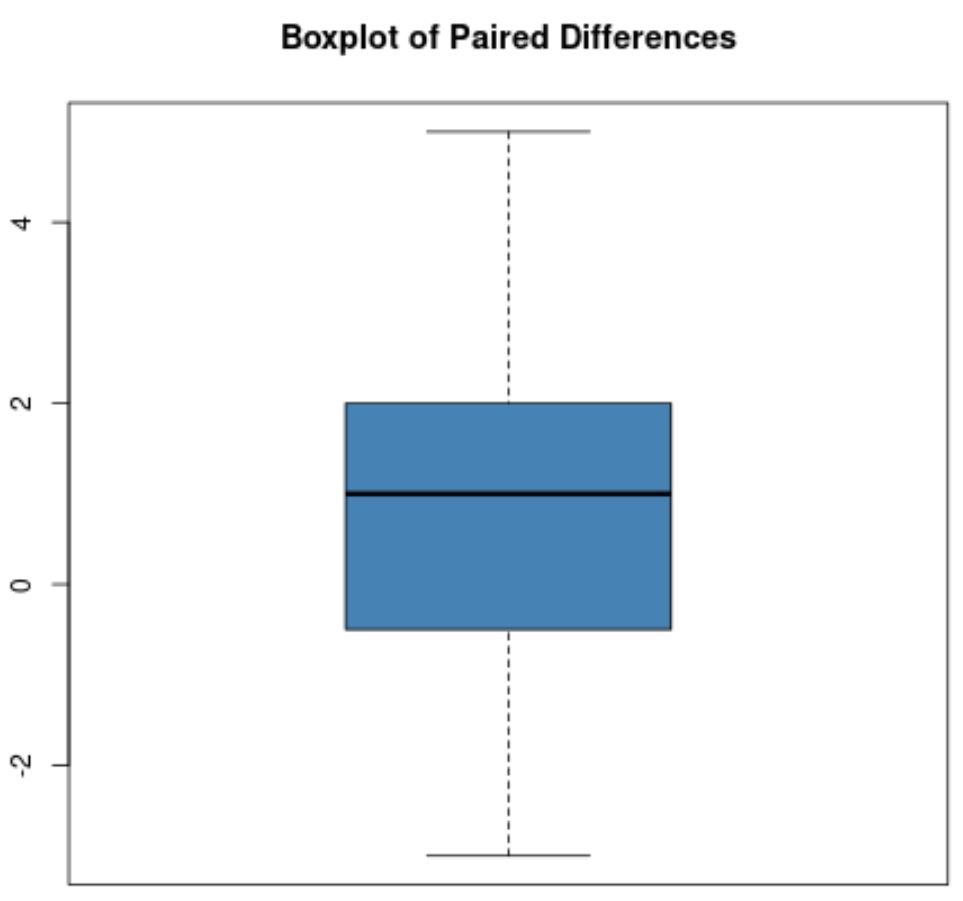
この箱ひげ図には明確な外れ値がないため、データには極端な外れ値がないと仮定します。
この前提が尊重されない場合はどうすればよいか
この仮定に違反すると、ペアになったサンプルの t 検定の結果が外れ値によって異常な影響を受ける可能性があります。
このシナリオでは、外れ値が欠陥のあるデータ ポイントを表している、またはデータ入力エラーの結果であると思われる場合は、外れ値を削除できます。
または、外れ値を保持し、対応のあるサンプルの t 検定の結果を報告するときに単にメモすることもできます。
追加リソース
次のチュートリアルでは、他の統計検定で行われた仮定について説明します。
t 検定で定式化された 4 つの仮説
カイ二乗検定の 4 つの仮説
パラメトリック テストの 4 つの仮説