Spss で対応のあるサンプルの t 検定を実行する方法

対のあるサンプルの t 検定は、一方のサンプルの各観測値がもう一方のサンプルの観測値と関連付けられる場合に、2 つのサンプルの平均を比較するために使用されます。

このチュートリアルでは、SPSS で対応のあるサンプルの t 検定を実行する方法を説明します。

例: SPSS での対応のあるサンプルの t 検定

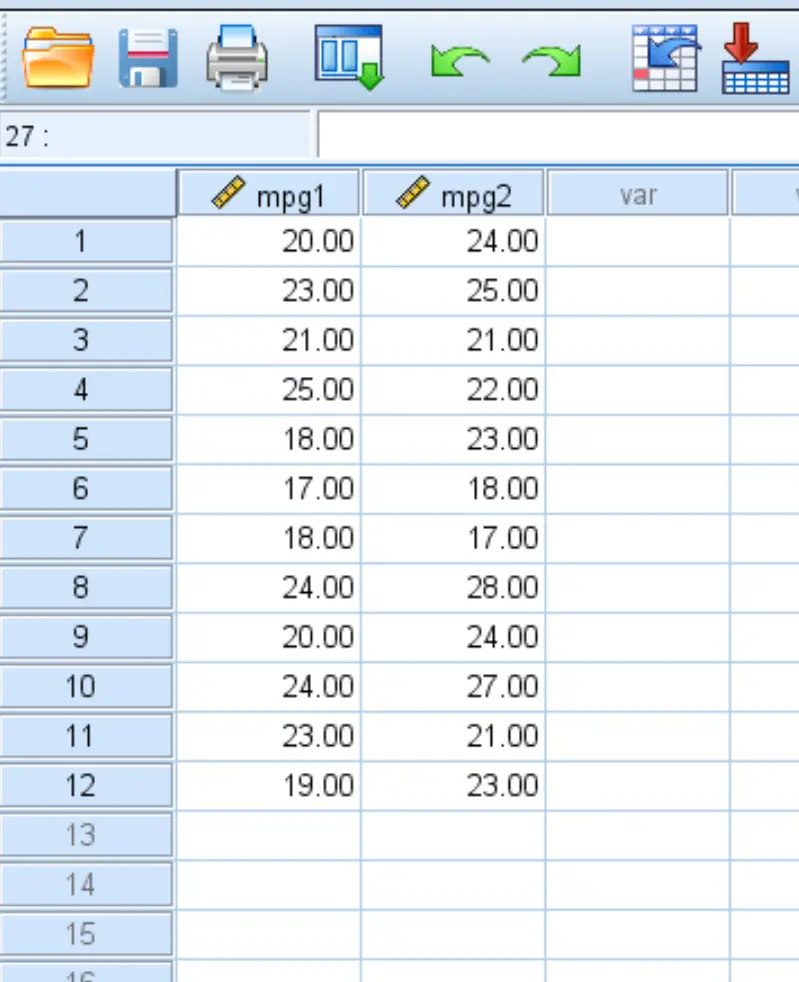
研究者は、新しい燃料処理によって特定の車の平均 mpg が変化するかどうかを知りたいと考えています。これをテストするために、燃料処理を行った場合と行わない場合の 12 台の車の燃費を測定する実験を実施しました。

各車が処理を受けるため、次の帰無仮説と対立仮説を使用して、各車がそれ自体とペアになっているペア t 検定を実行して、燃料処理の有無で平均 mpg に違いがあるかどうかを判断できます。

• H ₀ : μ ₁ = μ ₂ (2 つの母集団間の平均 mpg は等しい)
• H ₁ : μ ₁ ≠ μ ₂ (2 つの母集団間の平均 mpg は等しくない)

次のスクリーンショットは、燃料処理を行った場合 (mpg1) と燃料処理を行わなかった場合 (mpg2) の各車の mpg を示しています。

対応のある t 検定を実行するには、次の手順を実行します。

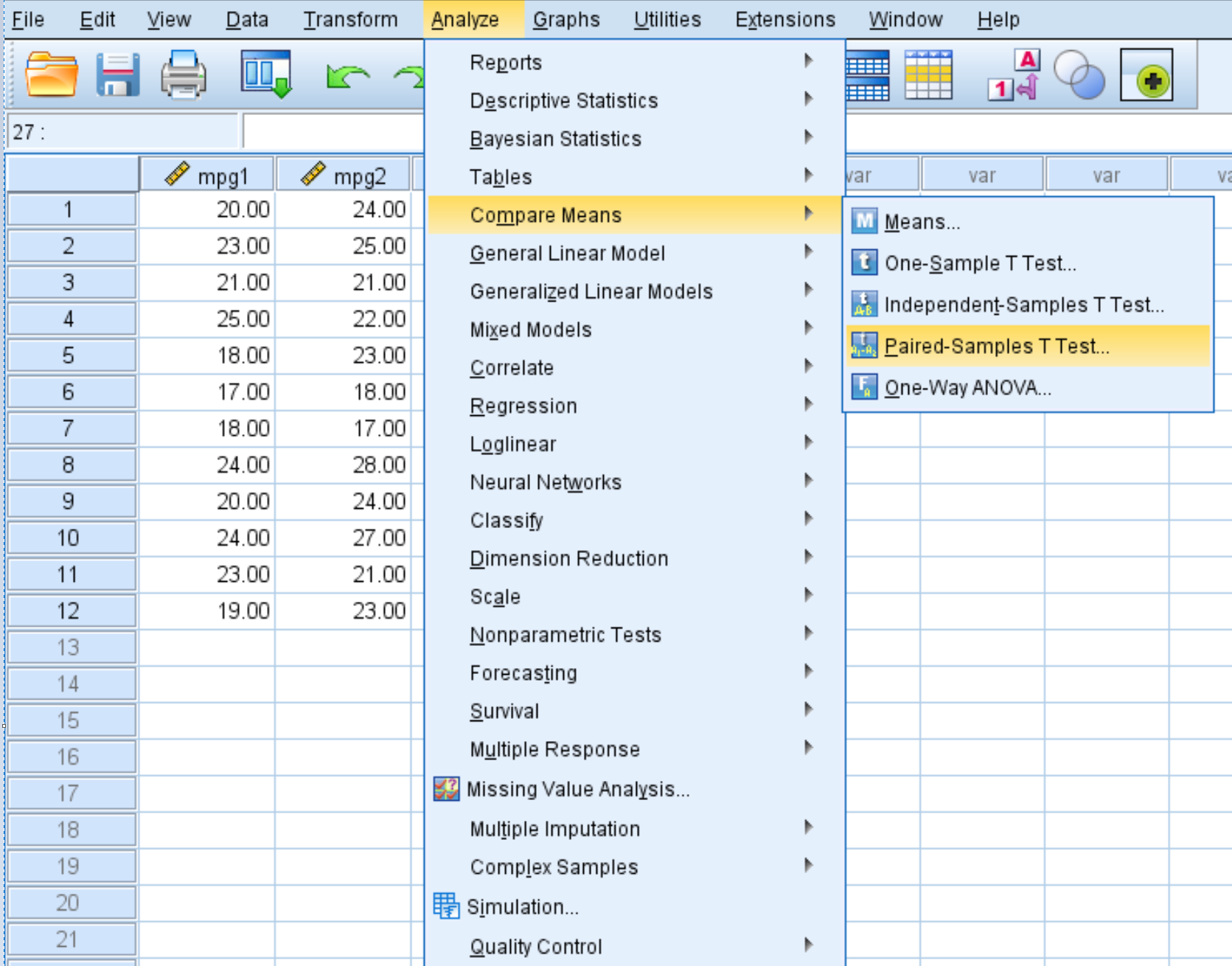
ステップ 1: [対応のあるサンプルの T 検定] オプションを選択します。

「分析」タブ、 「平均の比較」 、 「対応のあるサンプルの T 検定」の順にクリックします。

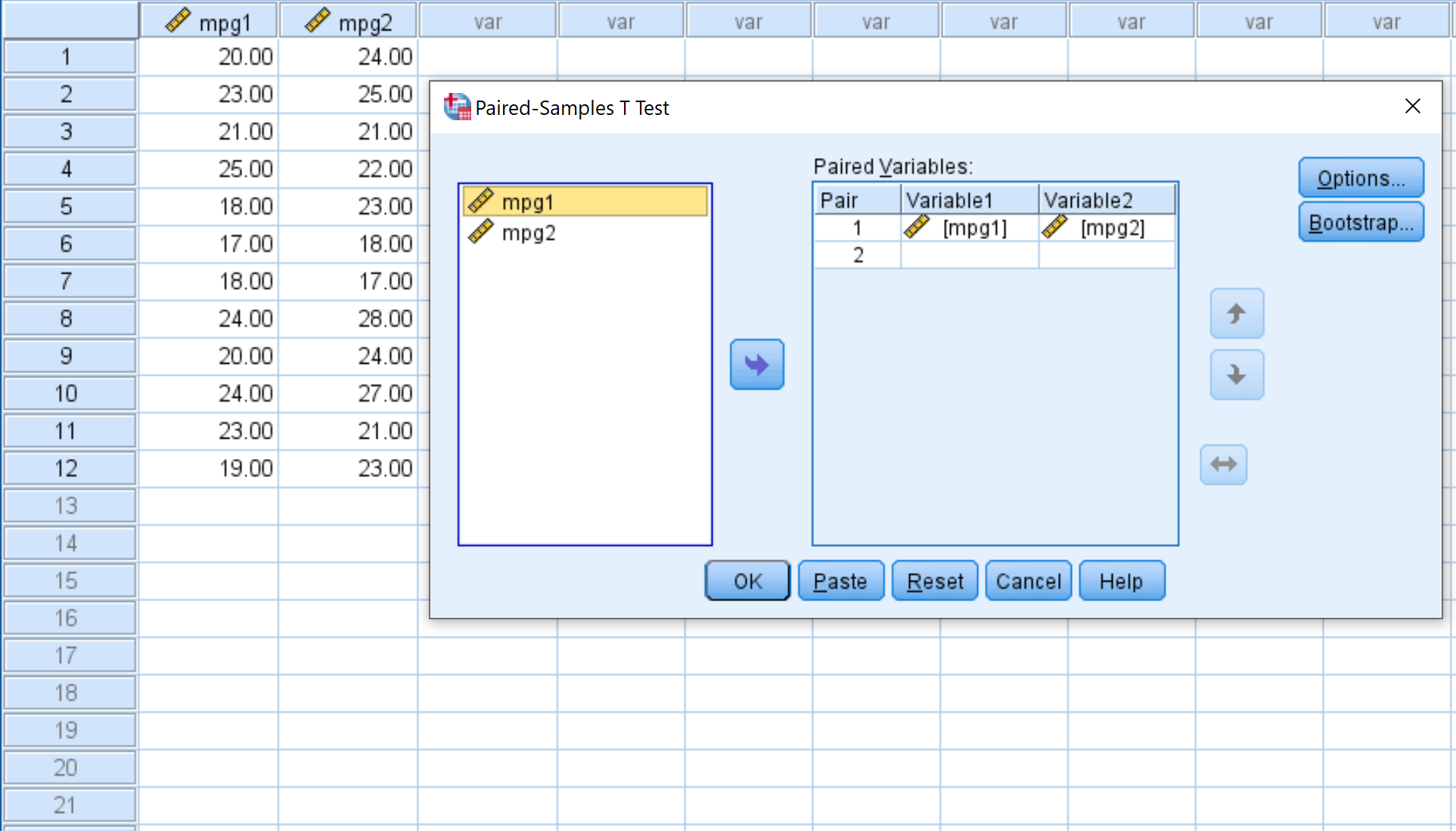
ステップ 2: テストを実行するために必要な値を入力します。

mpg1 を変数 1 の下のボックスにドラッグし、 mpg2 を変数 2 の下のボックスにドラッグします。次に、 「OK」をクリックします。

ステップ 3: 結果を解釈します。

[OK]をクリックすると、対応のあるサンプルの t 検定の結果が表示されます。

最初の表には、2 つのグループに関する次の概要統計が表示されます。

• N:各グループのサンプルサイズ
• 平均:各グループの車の平均 mpg
• 標準。偏差:各グループの車の燃費の標準偏差
• 標準。平均誤差:平均 mpg の標準誤差、s/√n で計算

最後の表は、対応のあるサンプルの t 検定の結果を示しています。

• t:検定統計量 (-2.244 であることが判明)
• df: #evens-1 = 12-1 = 11 として計算される自由度
• シグ。 (両側): df=11 の値 -2.244 に対応する両側 p 値

検定の p 値 (0.046) は 0.05 未満であるため、帰無仮説を棄却します。治療を受けた車と受けなかった車では真の平均燃費が異なると言える十分な証拠があります。

ステップ 4: 結果を報告します。

最後に、対応のある t 検定サンプルの結果を報告します。これを行う方法の例を次に示します。

新しい燃料処理によってガロンあたりの平均マイル数に違いが生じるかどうかを判断するために、12 台の車に対して対応のある t 検定が実行されました。

結果は、平均 mpg が 2 つのグループ間で有意水準 0.05 で統計的に異なることを示しました (t = -2.244、df=11、p = 0.046)。

母平均間の真の差の 95% 信頼区間は、区間 (-3.466, -0.034) となりました。