Ti-84 電卓で対数回帰を実行する方法

対数回帰は、成長または衰退が最初に急速に加速し、その後時間の経過とともに減速する状況をモデル化するために使用される回帰の一種です。

たとえば、次のグラフは対数減衰の例を示しています。

このタイプの状況では、予測変数と応答変数の間の関係は、対数回帰を使用して適切にモデル化できます。

対数回帰モデルの方程式は次の形式になります。

y = a + b*ln(x)

金：

• y:応答変数
• x:予測変数
• a、b: xとyの関係を説明する回帰係数

次の段階的な例は、TI-84 計算機で次のデータ セットに対して対数回帰を実行する方法を示しています。

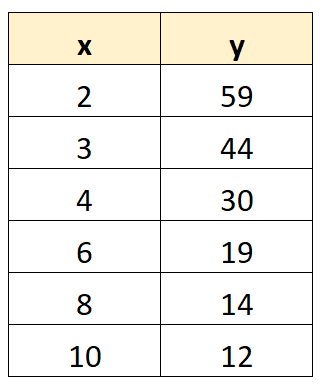
ステップ 1: データを入力する

まず、データ値を入力します。 STATを押してからEDITを押します。次に、データセットの x 値を列 L1 に入力し、y 値を列 L2 に入力します。

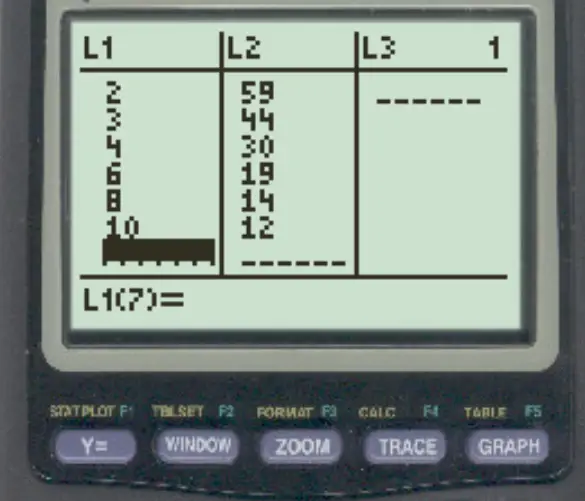
ステップ 2: 対数回帰モデルを当てはめる

次に、対数回帰モデルを埋めます。

[統計]をタップし、 [計算]までスクロールします。次に、 LnRegまでスクロールし、 ENTER を2 回押します。

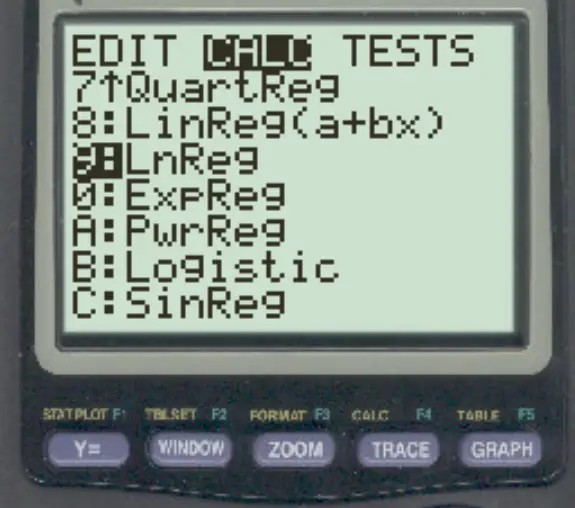
次の結果が表示されます。

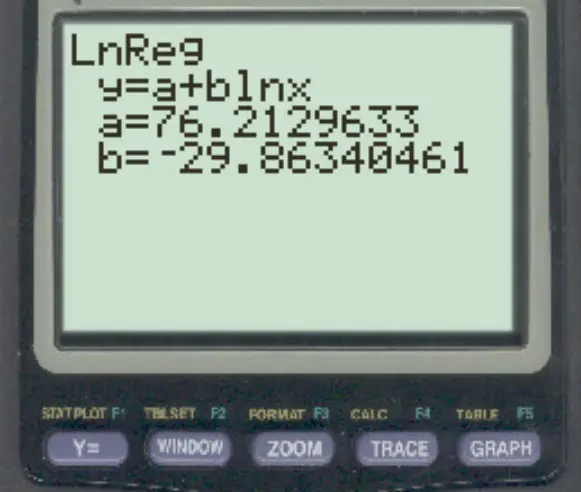
ステップ 3: 結果を解釈する

結果の係数を使用して、次の調整された対数回帰式を書くことができます。

y = 76.21296 – 29.8634 * ln(x)

この方程式を使用して、予測子変数xの値に基づいて応答変数yを予測できます。たとえば、 x = 8 の場合、 y は14.11になると予測します。

y = 76.21296 – 29.8634 * ln(8) = 14.11

ボーナス:このオンライン対数回帰計算ツールを自由に使用して、指定された予測子と応答変数の対数回帰式を自動的に計算できます。

追加リソース

TI-84 電卓で線形回帰を実行する方法
TI-84 電卓で二次回帰を実行する方法
TI-84 電卓で指数回帰を実行する方法
TI-84 電卓で残差プロットを作成する方法