Python での対数回帰 (ステップバイステップ)

対数回帰は、成長または衰退が最初に急速に加速し、その後時間の経過とともに減速する状況をモデル化するために使用される回帰の一種です。

たとえば、次のグラフは対数減衰の例を示しています。

このタイプの状況では、予測変数と応答変数の間の関係は、対数回帰を使用して適切にモデル化できます。

対数回帰モデルの方程式は次の形式になります。

y = a + b*ln(x)

金：

• y:応答変数
• x:予測変数
• a、b: xとyの関係を説明する回帰係数

次のステップバイステップの例は、Python で対数回帰を実行する方法を示しています。

ステップ 1: データを作成する

まず、2 つの変数xとyの偽のデータを作成しましょう。

 import numpy as np
x = np. arange (1, 16, 1)
y = np. array ([59, 50, 44, 38, 33, 28, 23, 20, 17, 15, 13, 12, 11, 10, 9.5])

ステップ 2: データを視覚化する

次に、簡単な散布図を作成して、 xとyの関係を視覚化しましょう。

 import matplotlib. pyplot as plt

plt. scatter (x,y)
plt. show () 

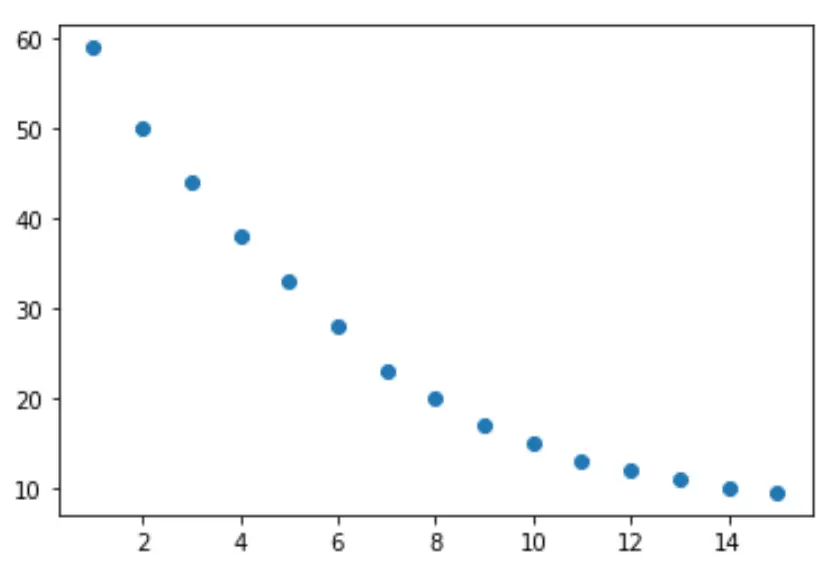
グラフから、2 つの変数間に対数減衰パターンがあることがわかります。応答変数yの値は、最初は急速に減少し、時間の経過とともに減少します。

したがって、対数回帰式を当てはめて変数間の関係を説明することが賢明であると思われます。

ステップ 3: 対数回帰モデルを当てはめる

次に、 polyfit()関数を使用して、 xの自然対数を予測変数として、 yを応答変数として使用して、対数回帰モデルを近似します。

 #fit the model
fit = np. polyfit (np. log (x), y, 1)

#view the output of the model
print(fit)

[-20.19869943 63.06859979]

結果の係数を使用して、次の調整された対数回帰式を書くことができます。

y = 63.0686 – 20.1987 * ln(x)

この方程式を使用して、予測子変数xの値に基づいて応答変数yを予測できます。たとえば、 x = 12 の場合、 y は12.87になると予測します。

y = 63.0686 – 20.1987 * ln(12) = 12.87

ボーナス:このオンライン対数回帰計算ツールを自由に使用して、指定された予測子と応答変数の対数回帰式を自動的に計算できます。

追加リソース

Python の線形回帰の完全ガイド
Python で指数回帰を実行する方法
Python でロジスティック回帰を実行する方法