対数尤度値を解釈する方法 (例付き)
回帰モデルの対数尤度値は、モデルの適合度を測定する方法です。対数尤度の値が高いほど、モデルはデータセットに適合します。
特定のモデルの対数尤度の値は、負の無限大から正の無限大までの範囲になります。特定のモデルの実際の対数尤度値は通常は意味がありませんが、 2 つ以上のモデルを比較する場合には役立ちます。
実際には、多くの場合、複数の回帰モデルをデータセットに適合させ、最も高い対数尤度値を持つモデルをデータに最も適合するモデルとして選択します。
次の例は、実際にさまざまな回帰モデルの対数尤度値を解釈する方法を示しています。
例: 対数尤度値の解釈
特定の地域にある 20 軒の異なる住宅の寝室の数、バスルームの数、販売価格を示す次のデータ セットがあるとします。
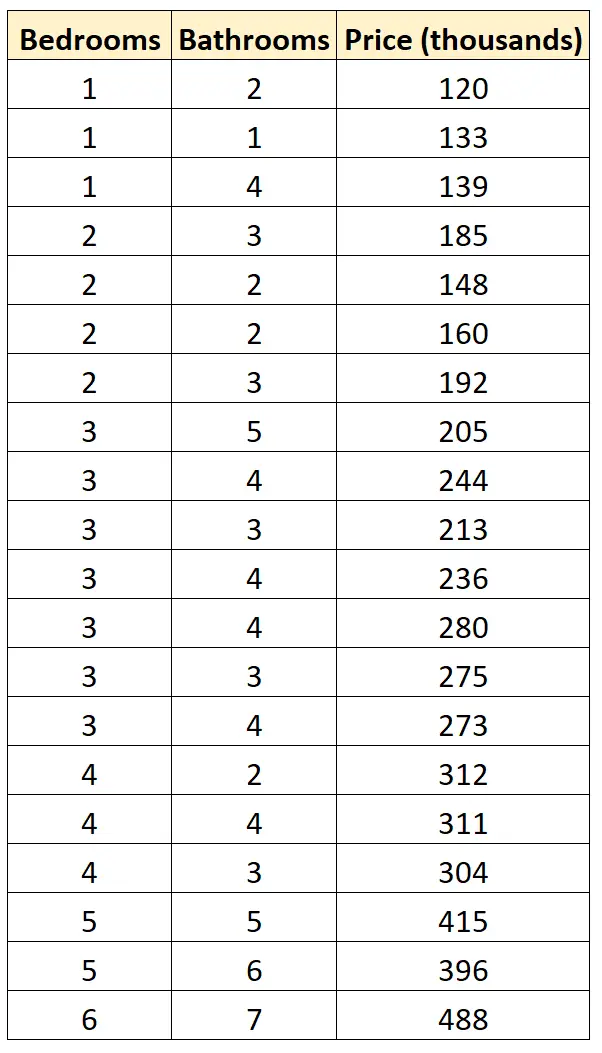
次の 2 つの回帰モデルを近似し、どちらがデータに最もよく適合するかを判断するとします。
モデル 1 : 価格 = β 0 + β 1 (部屋数)
モデル 2 : 料金 = β 0 + β 1 (浴室の数)
次のコードは、各回帰モデルを近似し、R で各モデルの対数尤度値を計算する方法を示しています。
#define data df <- data. frame (beds=c(1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 5, 5, 6), baths=c(2, 1, 4, 3, 2, 2, 3, 5, 4, 3, 4, 4, 3, 4, 2, 4, 3, 5, 6, 7), price=c(120, 133, 139, 185, 148, 160, 192, 205, 244, 213, 236, 280, 275, 273, 312, 311, 304, 415, 396, 488)) #fitmodels model1 <- lm(price~beds, data=df) model2 <- lm(price~baths, data=df) #calculate log-likelihood value of each model logLik(model1) 'log Lik.' -91.04219 (df=3) logLik(model2) 'log Lik.' -111.7511 (df=3)
最初のモデルの対数尤度値 ( -91.04 ) は 2 番目のモデル ( -111.75 ) よりも高く、最初のモデルの方がデータによりよく適合していることを意味します。
対数尤度値を使用する場合の注意事項
対数尤度値を計算する場合、追加の予測子変数が統計的に有意でなくても、モデルに追加の予測子変数を追加すると、ほとんどの場合、対数尤度値が増加することに注意することが重要です。
これは、各モデルの予測変数の数が同じである場合にのみ、2 つの回帰モデル間の対数尤度値を比較する必要があることを意味します。
予測変数の数が異なるモデルを比較するには、尤度比検定を実行して、2 つの入れ子になった回帰モデルの適合度を比較します。