対数正規分布

によるベンジャミン・アンダーソン博士 8月 3, 2023 確率 0コメント

この記事では、統計における対数正規分布とは何かについて説明します。したがって、対数正規分布とこのタイプの確率分布のグラフの特性が何であるかがわかります。

対数正規分布とは何ですか?

対数正規分布、または対数正規分布は、対数が正規分布に従う確率変数を定義する確率分布です。

したがって、変数 X が正規分布を持つ場合、指数関数 e ^{x は}対数正規分布になります。

$X\sim \text{Lognormal}(\mu,\sigma^2)$

対数は正の引数を 1 つだけ取る関数であるため、対数正規分布は変数値が正の場合にのみ使用できることに注意してください。

統計における対数正規分布のさまざまな用途の中で、この分布を金融投資の分析と信頼性分析の実行に使用することを区別します。

対数正規分布は、ティノー分布としても知られ、対数正規分布または対数正規分布とも呼ばれます。

対数正規分布のプロット

対数正規分布の定義がわかったので、このセクションでは、対数正規分布のグラフ表現が算術平均と標準偏差の値に応じてどのように変化するかを見ていきます。

対数正規分布の密度関数のグラフは次のとおりです。

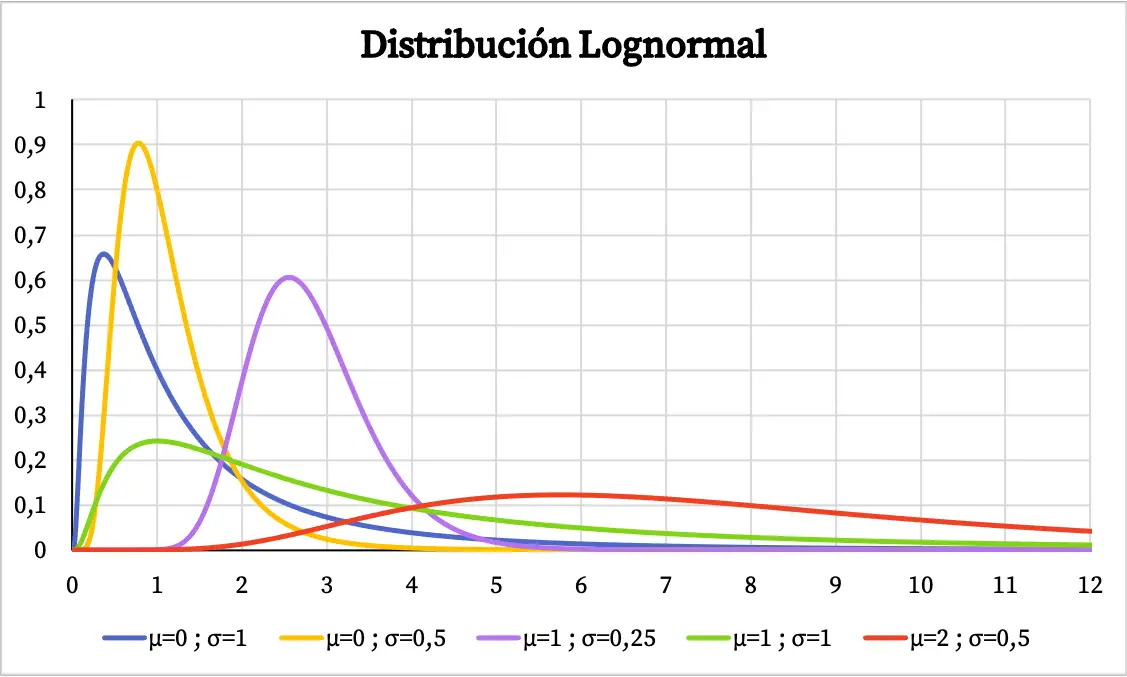
一方、対数正規分布の累積確率グラフは次のようになります。

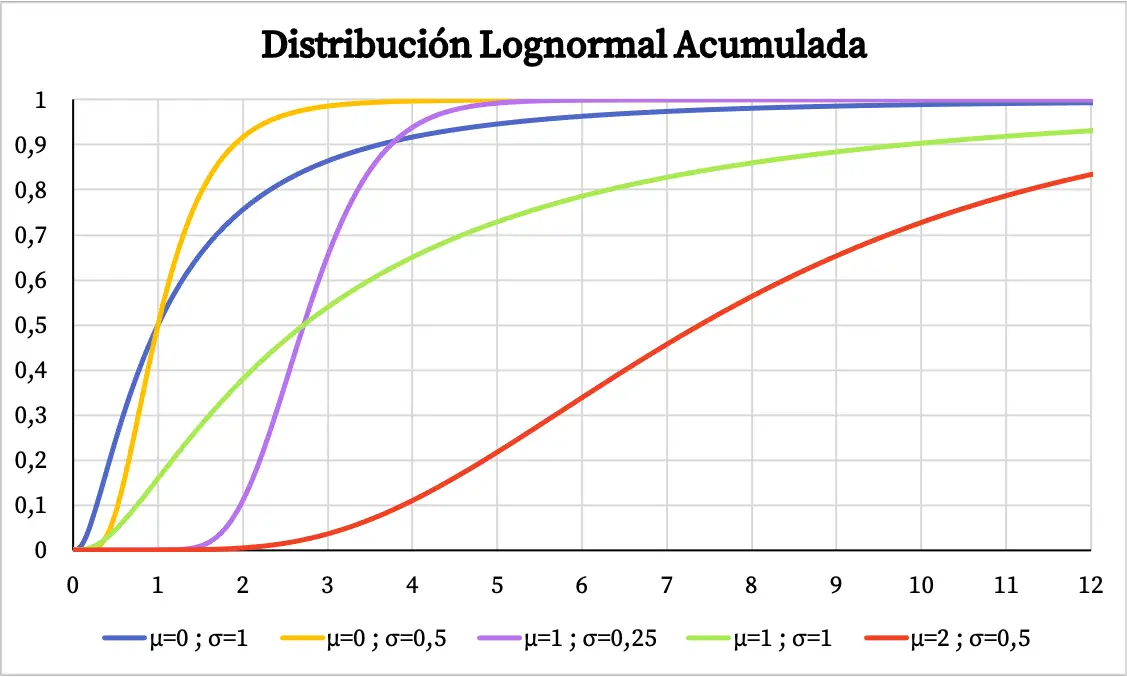
対数正規分布の特徴

対数正規分布には次の特徴があります。

対数正規分布は、2 つのパラメーターの値、算術平均 μ と分散 σ ²によって定義されます。

$X\sim \text{Lognormal}(\mu,\sigma^2)$

対数は負の値またはゼロの値を受け入れないため、対数正規分布の領域は正の実数で構成されます。

$x\in (0,+\infty)$

対数正規分布の期待値は、平均と分散の合計を 2 で割った数値 e に等しくなります。

$\displaystyle E[X]=e^{\mu+\frac{\sigma^2}{2}}$

一方、対数正規分布の分散は次の式で計算できます。

$Var(X)=\left(e^{\sigma^2}-1\right)\cdot e^{2\mu+\sigma^2$

対数正規分布の最頻値は、数値 e を分布の平均値まで累乗したものと等価です。

$Mo=e^\mu$

対数正規分布の歪度係数は、次の式を適用して決定できます。

$\displaystyle A=\left(e^{\sigma^2}+2\right)\cdot\sqrt{e^{\sigma^2}-1}$

対数正規分布の密度関数の式は次のとおりです。

$\displaystyle P[X=x]=\frac{1}{\sigma \cdot x\cdot \sqrt{2 \pi}}\cdot \exp\left(-\frac{(\ln x-\mu)^2}{2\sigma^2}\right)$

対数正規分布の累積確率関数の式は次のとおりです。

$\displaystyle P[X\leq x]=\Phi\left(\frac{\ln x-\mu}{\sigma}\right)$

金

$\Phi$

は、標準正規分布の累積確率関数です。

対数正規分布の算術平均は、その中央値よりも大きくなります。

$\mu > Me” title=”Rendered by QuickLaTeX.com” height=”16″ width=”61″ style=”vertical-align: -4px;”></p></p> </div>  <div class=$

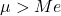
著者について

ベンジャミン・アンダーソン博士

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る

対数正規分布とは何ですか?

対数正規分布のプロット

対数正規分布の特徴

著者について

ベンジャミン・アンダーソン博士

コメントを追加する