リッジ回帰の概要

通常の重線形回帰では、 p 個の予測子変数のセットと応答変数を使用して、次の形式のモデルを近似します。

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

金：

• Y : 応答変数
• X _j : j^番目の予測変数
• β _j : 他のすべての予測子を固定したまま、X _jの 1 単位増加が Y に与える平均効果
• ε : 誤差項

β ₀ 、β ₁ 、B ₂ 、…、β _pの値は、残差の二乗和 (RSS) を最小化する最小二乗法を使用して選択されます。

RSS = Σ(y _i – ŷ _i ) ²

金：

• Σ : 和を意味するギリシャ語の記号
• y _i : ^{i 番目の}観測値の実際の応答値
• ŷ _i : 重回帰モデルに基づく予測応答値

ただし、予測変数の相関性が高い場合、 多重共線性が問題になる可能性があります。これにより、モデルの係数推定の信頼性が低くなり、大きな分散が示される可能性があります。

特定の予測子変数をモデルから完全に削除せずにこの問題を回避する 1 つの方法は、リッジ回帰として知られる方法を使用することです。この方法では、代わりに以下を最小限に抑えようとします。

RSS + λΣβ _j ²

ここで、j は1 からpまで変化し、 λ ≥ 0 となります。

方程式のこの 2 番目の項は、撤退ペナルティとして知られています。

λ = 0 の場合、このペナルティ項は効果がなく、リッジ回帰は最小二乗法と同じ係数推定値を生成します。ただし、λ が無限大に近づくと、収縮ペナルティの影響が大きくなり、回帰係数のピーク推定値はゼロに近づきます。

一般に、モデル内で最も影響力の少ない予測子変数は、最も速くゼロに向かって減少します。

リッジ回帰を使用する理由

最小二乗回帰に対するリッジ回帰の利点は、 バイアスと分散のトレードオフです。

平均二乗誤差 (MSE) は特定のモデルの精度を測定するために使用できるメトリクスであり、次のように計算されることを思い出してください。

MSE = Var( f̂( x ₀ )) + [バイアス( f̂( x ₀ ))] ² + Var(ε)

MSE = 分散 + バイアス² + 既約誤差

リッジ回帰の基本的な考え方は、分散を大幅に低減できるように小さなバイアスを導入し、全体的な MSE を下げることです。

これを説明するために、次のグラフを考えてみましょう。

λ が増加すると、バイアスがわずかに増加するだけで分散が大幅に減少することに注意してください。ただし、ある点を超えると、分散の減少速度が鈍くなり、係数の減少により係数が大幅に過小評価され、バイアスが急激に増加します。

グラフから、バイアスと分散の間の最適なトレードオフを生み出す λ の値を選択すると、テストの MSE が最も低くなることがわかります。

λ = 0 の場合、リッジ回帰のペナルティ項は効果がないため、最小二乗法と同じ係数推定値が生成されます。ただし、λ を特定の点まで増やすことによって、テスト全体の MSE を減らすことができます。

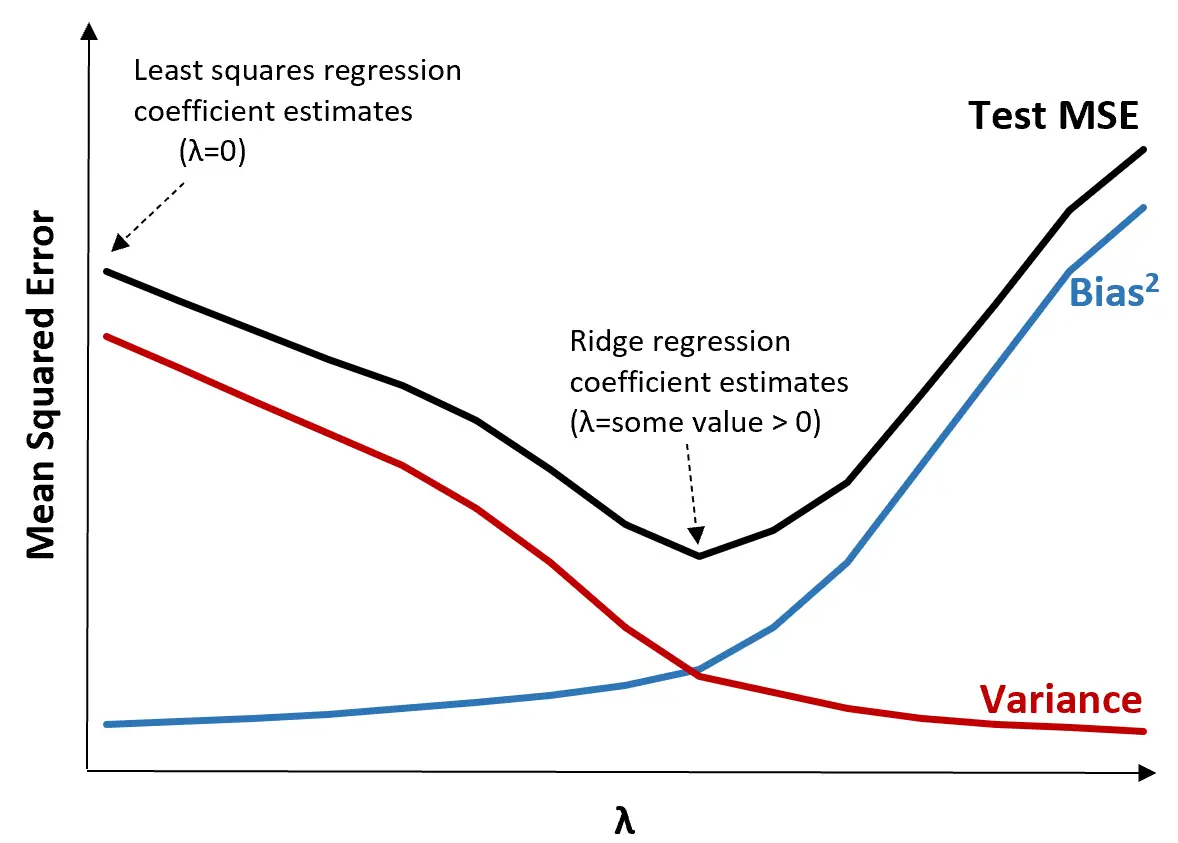
これは、リッジ回帰によるモデル フィッティングの方が、最小二乗回帰によるモデル フィッティングよりも小さなテスト誤差が生じることを意味します。

実際にリッジ回帰を実行する手順

次の手順を使用してリッジ回帰を実行できます。

ステップ 1: 予測子変数の相関行列と VIF 値を計算します。

まず、 相関行列を作成し、各予測変数のVIF (分散膨張係数) 値を計算する必要があります。

予測変数と高い VIF 値の間に強い相関関係が検出された場合 (一部のテキストでは「高い」VIF 値を 5 と定義していますが、他のテキストでは 10 を使用しています)、おそらくリッジ回帰が適切です。

ただし、データに多重共線性がない場合は、そもそもリッジ回帰を実行する必要がない場合があります。代わりに、通常の最小二乗回帰を実行できます。

ステップ 2: 各予測変数を標準化します。

リッジ回帰を実行する前に、各予測子変数の平均が 0、標準偏差が 1 になるようにデータをスケーリングする必要があります。これにより、リッジ回帰の実行時に単一の予測子変数が過剰な影響を及ぼさないことが保証されます。

ステップ 3: リッジ回帰モデルを適合させ、λ の値を選択します。

λ にどの値を使用するかを決定するために使用できる正確な公式はありません。実際には、λ を選択するには 2 つの一般的な方法があります。

(1) リッジトレースプロットを作成します。これは、λが無限大に向かって増加するときの係数推定値の値を視覚化したグラフです。通常、ほとんどの係数推定値が安定し始める値として λ を選択します。

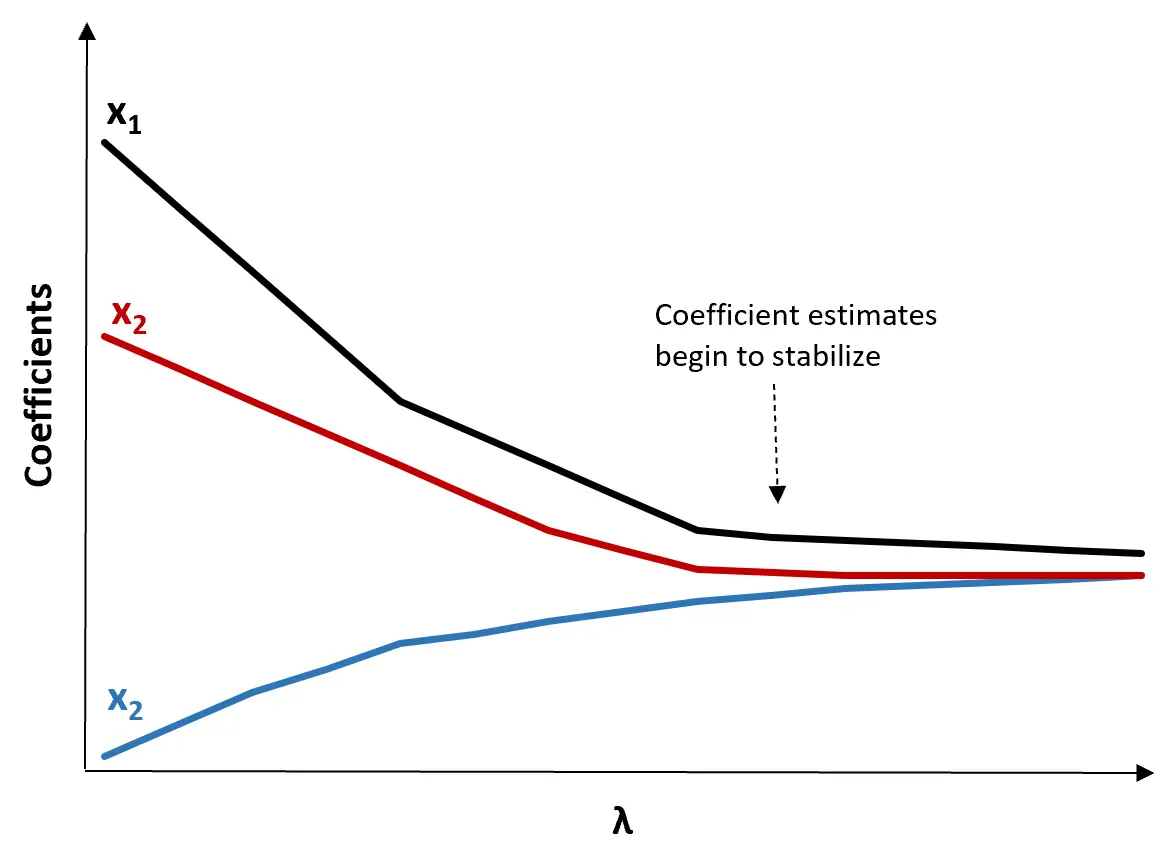
(2) λ の各値に対する MSE テストを計算します。

λ を選択するもう 1 つの方法は、さまざまな λ の値を使用して各モデルのテスト MSE を単純に計算し、最も低いテスト MSE を生成する値として λ を選択することです。

リッジ回帰の長所と短所

リッジ回帰の最大の利点は、多重共線性が存在する場合に最小二乗法よりも低い検定平均二乗誤差 (MSE) を生成できることです。

ただし、リッジ回帰の最大の欠点は、最終モデルにすべての予測子変数が含まれるため、変数選択を実行できないことです。一部の予測変数はゼロに非常に近く減少するため、モデルの結果の解釈が困難になる可能性があります。

実際には、リッジ回帰は最小二乗モデルと比較してより適切な予測ができるモデルを生成する可能性がありますが、多くの場合、モデルの結果を解釈するのがより困難になります。

モデルの解釈と予測精度のどちらが重要であるかに応じて、さまざまなシナリオで通常の最小二乗法またはリッジ回帰の使用を選択できます。

R と Python のリッジ回帰

次のチュートリアルでは、リッジ回帰モデルのフィッティングに最も一般的に使用される 2 つの言語である R と Python でリッジ回帰を実行する方法について説明します。

R でのリッジ回帰 (ステップバイステップ)
Python でのリッジ回帰 (ステップバイステップ)