平均値の仮説検定
この記事では、統計学における平均値の仮説検定とは何かについて説明します。したがって、平均に対する仮説検定の公式と、ステップごとに解決される演習が見つかります。
平均値の仮説検定とは何ですか?
平均値の仮説検定は、母集団平均値の帰無仮説を棄却または棄却するために使用される統計的手法です。
より具体的には、平均値の仮説検定には、検定統計量を計算し、それを臨界値と比較して帰無仮説を棄却するかどうかが含まれます。
仮説検定には異なる名前があることに注意してください。統計学では、仮説対比、仮説検定、または有意性検定とも呼ばれます。
平均値の仮説検定式
次に、平均の仮説検定統計量がどのように計算されるかを見ていきます。ただし、分散が既知であるかどうかによって計算式が若干異なるため、最初に分散が既知の場合と分散が未知の場合の計算方法を見ていきます。
既知の偏差あり
既知の分散を使用した平均の検定仮説の式は次のとおりです。

金:
-

は平均に対する仮説検定統計量です。
-

はサンプル平均です。
-

は提案された平均値です。
-

は母集団の標準偏差です。
-

はサンプルサイズです。
平均の仮説検定統計量が計算されると、その結果は帰無仮説を棄却または棄却すると解釈される必要があります。
- 平均値の仮説検定が両側である場合、統計量の絶対値が臨界値 Z α/2より大きい場合、帰無仮説は棄却されます。
- 平均の仮説検定が右裾に一致する場合、統計量が臨界値 Z αより大きい場合、帰無仮説は棄却されます。
- 平均の仮説検定が左裾に一致する場合、統計量が臨界値 -Z αより小さい場合、帰無仮説は棄却されます。
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0e2ccadfc369eb7543b8f86dfccc528e_l3.png)
この場合、臨界値は標準化正規分布表から取得されます。
不明な分散あり
分散が不明な平均に対する検定仮説の式は次のとおりです。

金:
-

は、平均の仮説検定統計量であり、スチューデントの t 分布によって定義されます。
-

はサンプル平均です。
-

は提案された平均値です。
-

は標本標準偏差です。
-

はサンプルサイズです。
前と同様に、帰無仮説を棄却するかどうかを決定するには、検定統計量の計算結果を臨界値で解釈する必要があります。
- 平均値の仮説検定が両側である場合、統計量の絶対値が臨界値 t α/2|n-1より大きい場合、帰無仮説は棄却されます。
- 平均の仮説検定が右裾に一致する場合、統計量が臨界値 t α|n-1より大きい場合、帰無仮説は棄却されます。
- 平均の仮説検定が左裾に一致する場合、統計量が臨界値 -t α|n-1より小さい場合、帰無仮説は棄却されます。
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-31fb206b75a47181c7c673f54ba28ee8_l3.png)
分散が不明な場合、臨界検定値はスチューデントの分布表から取得されます。
平均値の仮説検定の実世界の例
母平均に対する仮説検定の概念を完全に理解するために、このタイプの仮説検定の実際の例を以下に示します。
- あるテクノロジー企業は、自社が販売するラップトップのバッテリーは 6 時間持続すると主張しています。有意水準 α = 0.05 で仮説検定を実行することで、この仮説が偽であるかどうかを確認します。これを行うために、20 ユニットを購入し、各コンピューターのバッテリー寿命を観察することにしました (値は時間で表されます)。
5.2 5.9 7.1 4.2 6.5
8.5 4.6 6.8 6.9 5.8
5.1 6.5 7.0 5.3 6.2
5.7 6.6 7.5 5.1 6.1
この場合、平均に関する仮説検定の帰無仮説と対立仮説は次のとおりです。
![Rendered by QuickLaTeX.com \begin{cases}H_0: \mu=6\\[2ex] H_1:\mu\neq 6 \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-329ffe392783b8bee1eef642d1a45f53_l3.png)
検定統計量を決定するには、まずサンプル平均とサンプル標準偏差を計算する必要があります。
![]()
母集団の分散がわからないため、検定統計量を取得するには、分散が不明な平均に対する仮説検定式を適用する必要があります。

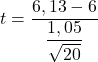
![]()
次に、仮説検定の臨界値を見つける必要があるため、スチューデントの t 分布表で対応する値を調べます。スチューデントの t の自由度はサンプル サイズより 1 つ小さく (20-1=19)、一方、両側であるため、対応する確率は有意水準の半分 (0.05/2= 0.025) になります。仮説検証。
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n-1}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 19}=2,093\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e85692dfb2fb2522025566dc205b8117_l3.png)
結論として、これは両側仮説検定であり、検定統計量の絶対値が臨界値より小さいため、帰無仮説は棄却されませんが、対立仮説は棄却されます。
![]()
平均値の違いに関する仮説検定
平均仮説検定の差は、 2 つの母集団の平均が同じであるという帰無仮説を棄却または受け入れるために使用されます。
したがって、2 つの平均の差に対する仮説検定の帰無仮説は常に次のようになります。
![]()
一方、対立仮説は次の 3 つのいずれかになります。
![Rendered by QuickLaTeX.com \begin{array}{l}H_1:\mu_1\neq \mu_2\\[2ex]H_1:\mu_1>\mu_2\\[2ex]H_1:\mu_1<\mu_2\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-c612ac7651faad9faa195f37fdf6edef_l3.png)
次に、分散が既知の場合に平均の差の仮説検定統計量を計算する式は次のとおりです。
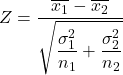
金:
-

は、標準正規分布に従う、分散が既知の 2 つの平均の差の仮説検定統計量です。
-

はサンプル 1 の平均です。
-

はサンプル 2 の平均です。
-

は母集団 1 の分散です。
-

は母集団 2 の分散です。
-

サンプルサイズは1です。
-

サンプルサイズは2です。
一方、分散が不明な場合の平均の差の仮説検定統計量を計算する式は次のとおりです。
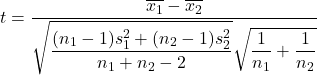
金:
-

は、分散が不明な 2 つの平均の差の仮説検定統計量であり、スチューデントの t 分布に従います。
-

はサンプル 1 の平均です。
-

はサンプル 2 の平均です。
-

はサンプル 1 の分散です。
-

はサンプル 2 の分散です。
-

サンプルサイズは1です。
-

サンプルサイズは2です。