平均値の違いに関する仮説検定
この記事では、統計における平均値の仮説検定とはどのような違いがあるのか、また何に使用されるのかについて説明します。同様に、平均値の違いに関する仮説検定と、段階的に解決する演習を行う方法もわかります。
平均差の仮説検定とは何ですか?
平均値の差に関する仮説検定は、 2 つの母集団の平均値が異なるという仮説を棄却または受け入れるために使用される統計検定です。つまり、平均値仮説検定の差を使用して、2 つの母集団の平均値が同じか異なるかを判断します。
仮説検定で行われる決定は、以前に確立された信頼レベルに基づいて行われるため、仮説検定の結果が常に正しいことを保証することはできません。むしろ、それが真である可能性が最も高い結果であるということを念頭に置いてください。
2 つの平均の差の仮説検定には、検定統計量を計算し、それを臨界値と比較して帰無仮説を棄却するかどうかが含まれます。以下では、平均の差に対する仮説検定を実行する方法を見ていきます。
最後に、統計学では、仮説検定は仮説対比、仮説検定、または有意性検定と呼ばれることもあることを覚えておいてください。
平均値の差の仮説検定式
平均の差に関する仮説を検定するために使用する公式は、母集団の分散が既知であるかどうか、また、既知でない場合はそれらが同じであると仮定できるか、または異なると仮定できるかによって異なります。したがって、このセクションでは、ケースに応じてどの公式を使用するかを見ていきます。
既知のバリエーション
分散が既知の場合に、平均の差の仮説検定統計量を計算する式は次のとおりです。

金:
-

は、標準正規分布に従う、分散が既知の 2 つの平均の差の仮説検定統計量です。
-

は母集団 1 の平均です。
-

は母集団 2 の平均です。
-

はサンプル 1 の平均です。
-

はサンプル 2 の平均です。
-

は母集団 1 の標準偏差です。
-

は母集団 2 の標準偏差です。
-

サンプルサイズは1です。
-

サンプルサイズは2です。
これは最も一般的なケースではないため、この式は一部の特定のケースでのみ使用されることに注意してください。
未知の等しい偏差
母集団の分散が不明であるが等しいと仮定される場合、平均の差の仮説検定統計量を計算する式は次のとおりです。

金:
-

は、未知の分散を伴う平均の差の仮説検定統計量であり、自由度 n 1 + n 2 -2 のスチューデントの t 分布に従います。
-

は母集団 1 の平均です。
-

は母集団 2 の平均です。
-

はサンプル 1 の平均です。
-

はサンプル 2 の平均です。
-

は結合された標準偏差です。
-

サンプルサイズは1です。
-

サンプルサイズは2です。
2 つのサンプルの標準偏差を組み合わせた値は、次の式で計算されます。

未知のさまざまなバリエーション
母集団の分散が不明で、さらに異なると仮定される場合、平均の差に対する仮説検定統計量を計算する式は次のとおりです。

金:
-

は、未知の分散を伴う平均の差の仮説検定統計量であり、スチューデントの t 分布に従います。
-

は母集団 1 の平均です。
-

は母集団 2 の平均です。
-

はサンプル 1 の平均です。
-

はサンプル 2 の平均です。
-

は母集団 1 の標準偏差です。
-

は母集団 2 の標準偏差です。
-

サンプルサイズは1です。
-

サンプルサイズは2です。
ただし、この場合、スチューデントの t 分布の自由度は次の式を使用して計算されます。

平均値の違いに対する仮説検定の具体例
平均の差に関する仮説検定の概念を理解するために、このタイプの仮説検定の具体的な例を見ていきます。
- 競合する 2 つの企業の給与に関する統計調査を行いたいと考えています。具体的には、2 つの企業の平均給与が異なるかどうかを判断したいと考えています。これを行うために、ある会社から 47 人の労働者のサンプルを採取し、もう 1 つの会社から 55 人の労働者のサンプルを採取します。最初のサンプルからは平均給与 40,000 ドルと標準偏差 12,000 ドルが得られ、2 番目のサンプルからは平均給与 46,000 ドルと標準偏差 18,000 ドルが得られます。 5% の有意水準で仮説検定を実行して、平均給与が異なるかどうかを判断します。
この場合、2 つの平均の差に対する仮説検定の帰無仮説と対立仮説は次のとおりです。
![Rendered by QuickLaTeX.com \begin{cases}H_0: \mu_1-\mu_2=0\\[2ex] H_1:\mu_1-\mu_2\neq 0 \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-4dd9e80c0a87987d689d7b8d99be9d90_l3.png)
この場合、人口格差は不明ですが、両社は競合企業であり、事業を展開する市場の労働条件が非常に似ているため、人口格差は等しいと想定できます。したがって、使用すべき平均の差の仮説検定統計量の式は次のとおりです。

したがって、2 つのサンプルのプールされた標準偏差を計算します。
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(47-1)\cdot 12000^2+(55-1)\cdot 18000^2}{47+55-2}}\\[2ex]s_p&=15530,61\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0308363d68c4677761d44b214b1609d9_l3.png)
ここで、平均の差に仮説検定公式を適用します。
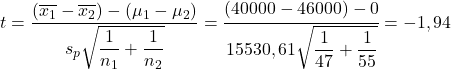
一方、スチューデントの t テーブルの平均の差に対する仮説検定の臨界値を探します。
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 100}=1,984\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d5f11ecd0336e50c63b0ab2fab4bd530_l3.png)
次に、検定統計量の絶対値が臨界検定値より小さいため、帰無仮説が受け入れられ、対立仮説が棄却されます。
![]()