平均値の差の信頼区間
この記事では、統計における平均値の差の信頼区間とは何か、またその用途について説明します。したがって、2 つの平均値の差の信頼区間を計算する方法と、段階的に解決される演習を理解できます。
平均値の差の信頼区間はどれくらいですか?
平均値の差の信頼区間は、 2 つの母集団の平均値の差の値が一定の信頼度で収まる最大値と最小値を提供する区間です。
たとえば、95% の信頼水準を持つ 2 つの母集団の平均値の差の信頼区間が (3.5) である場合、これは、2 つの母集団の平均値の差が 95 の確率で 3 ~ 5 の間にあることを意味します。 %。
したがって、統計では、平均値の差の信頼区間は、2 つの母集団平均値間の差が存在する 2 つの値を推定するために使用されます。したがって、2 つのサンプルからのデータを使用すると、母集団平均間の差を近似することができます。
平均値の差の信頼区間の公式
平均値の差の信頼区間の式は、母集団の分散が既知であるかどうか、また、既知でない場合は母集団の分散が等しいと仮定できるかどうかによって異なります。 。次に、それぞれのケースで平均の差の信頼区間がどのように計算されるかを見ていきます。
既知の偏差
2 つの母集団の分散が信頼水準 1-α で既知である場合に、平均の差の信頼区間を計算する式は次のとおりです。
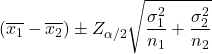
金:
-

はサンプル i の平均です。
-

は母集団 i の標準偏差です。
-

は、確率 α/2 の標準正規分布の値です。
-

はサンプルサイズ i です。
母集団分散の値は一般に不明であるため、このケースは最も一般的ではありません。
未知の等分散
2 つの母集団の分散が不明だが等しいと推定できる場合、信頼水準 1-α で平均の差の信頼区間を計算する式は次のとおりです。
![]()
金:
-

はサンプル i の平均です。
-

プールされた標準偏差です。
-

は、確率 α/2 の n 1 + n 2 -2 自由度のスチューデント t 分布の値です。
-

はサンプルサイズ i です。
この場合、母集団の分散は等しいと想定されているため、結合標準偏差を使用して信頼区間が計算されます。信頼区間は次の式で計算されます。

金
![]()
はサンプル i の標準偏差です。
未知のさまざまなバリエーション
2 つの母集団の分散が不明で、等しいと想定できない場合、信頼水準 1-α で平均の差の信頼区間を計算する式は次のとおりです。
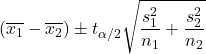
金:
-

はサンプル i の平均です。
-
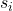
はサンプル i の標準偏差です。
-

は、確率 α/2 のスチューデントの t 分布の値です。
-

はサンプルサイズ i です。
この場合、スチューデントの t 分布の自由度は次の式を使用して計算されます。

金
![]()
はサンプル i の標準偏差です。
平均値の差の信頼区間の具体例
平均の差の信頼区間の定義とさまざまな式が何であるかを理解した後、2 つの平均の差の信頼区間がどのように計算されるかを理解する具体的な例を見ていきます。
- 私たちは子供の出生体重に対するタバコの影響を研究したいと考えています。これを行うために、2 つのサンプルが比較されます。最初のサンプルは母親が喫煙していない子供から構成され、2 番目のサンプルは母親が喫煙している子供から構成されます (サンプルのパラメーターは以下に示されています)。信頼水準 95% で平均の差の信頼区間を計算します。
- 非喫煙者の母親:
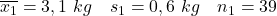
- 喫煙する母親:
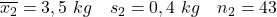
- 非喫煙者の母親:
この場合、母集団の分散の値はわかりませんが、非常によく似た特性を持つ 2 つの母集団を扱っているため、母集団の分散は等しいと仮定できます。したがって、使用すべき平均値の差の信頼区間の式は次のとおりです。
![]()
したがって、2 つのサンプルの標準偏差から結合標準偏差を計算します。
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(39-1)\cdot 0,6^2+(43-1)\cdot 0,4^2}{39+43-2}}\\[2ex]\displaystyle s_p&=0,50\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-688958252e9838e7fddc2ddcb9061b01_l3.png)
同様に、スチューデントの t 分布の確率分布表で、80 自由度のスチューデントの t 分布の値を 2.5% の確率で見つける必要があります。
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025|80}=1,990\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5e4ea90fdc33c9a3d3dab0f1d9d29af0_l3.png)
最後に、平均の差の信頼区間の式にデータを代入し、計算を実行します。
![]()
![]()
![]()
したがって、問題の平均値の差の信頼区間は次のようになります。
![]()