統計において平均が重要なのはなぜですか?
データセットの平均は、データセットの平均値を表します。次のように計算されます。
平均 = Σx i / n
金:
- Σ: 「和」を意味する記号
- x i :データセット内の i番目の観測値
- n:データセット内の観測値の総数
たとえば、11 個の観測値を含む次のデータセットがあるとします。
データセット: 3、4、4、6、7、8、12、13、15、16、17
データセットの平均は次のように計算されます。
平均 = (3+4+4+6+7+8+12+13+15+16+17) / 11 = 9.54
統計では、次の理由から平均が重要です。
1.平均により、データセットの「中心」がどこにあるのかがわかります。
2.平均値の計算方法により、平均値にはデータセット内の各観測値からの情報が含まれます。
次の例は、これら 2 つの理由を示しています。
例: データセットの平均を計算する
ある都市の 10,000 戸の異なる住宅の販売価格を含むデータセットがあるとします。

何千行もの生データを調べる代わりに、平均値を計算して、その都市の住宅の平均販売価格をすぐに把握できます。
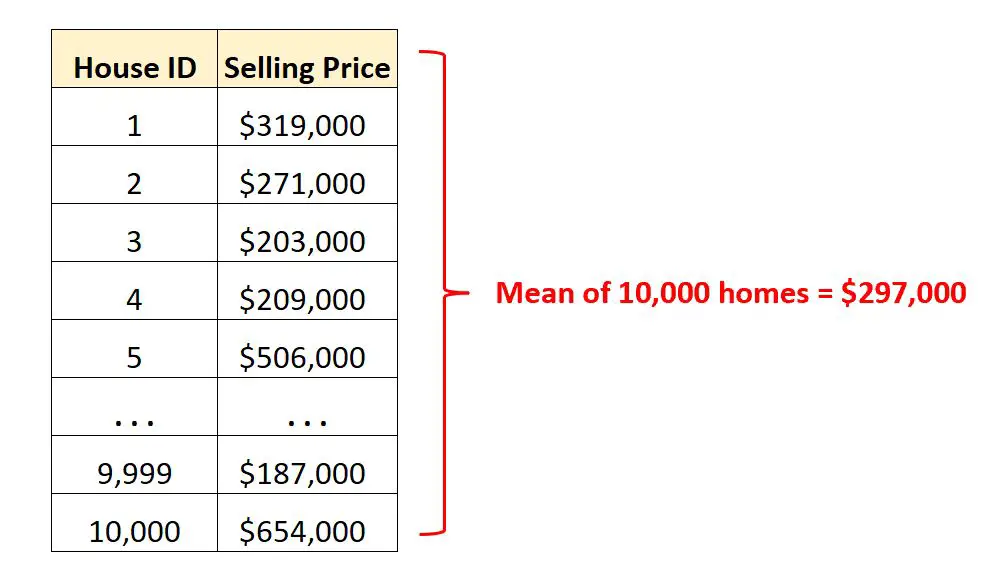
平均販売価格が 297,000 ドルであることを知ると、この都市での「典型的な」住宅がいくらで販売されるかがわかります。
この単一の平均値は、生データのすべての行を調べるよりも解釈がはるかに簡単です。
各住宅の販売価格は平均の計算に使用されたため、平均販売価格に住宅の総数を乗算して、その都市のすべての住宅の販売価格の合計を求めることができます。
- 全住宅の販売価格の合計 = 平均販売価格 * 住宅の数
- すべての住宅の合計販売価格 = 297,000 ドル * 10,000
- 全住宅の総販売価格 = 29 億 7,000 万ドル
この都市のすべての住宅の販売価格の合計は 29 億 7,000 万ドルであることがわかります。
平均を使用する場合
データセットを分析するとき、中心的な値がどこにあるのかを理解したいと思うことがよくあります。
統計では、データセットの中心を測定するために使用する一般的な指標が 2 つあります。
- Mean : 一連のデータの平均値
- Median : データセット内の中央値
平均はデータ セットの中心を測定する最も一般的な方法ですが、実際には次の状況では誤解を招く可能性があります。
これを説明するために、次の 2 つの例を考えてみましょう。
例 1: 偏った分布の平均を計算する
特定の都市の住民の給与の次の分布を考えてみましょう。

分布の右側にある賃金が高いと、平均が分布の中心から遠ざかります。
したがって、分布が右に偏っているため、中央値は平均よりも居住者の「典型的な」給与をよりよく反映しています。
この特定の例では、平均給与は 47,000 ドルですが、中央値は 32,000 ドルです。
したがって、中央値はその都市の典型的な給与をよりよく表しています。
例 2: 外れ値が存在する場合の平均値の計算
特定の通りにある住宅の面積を示す次のグラフを考えてみましょう。

平均値は少数の非常に大きな住宅に大きく影響されますが、中央値は影響を受けません。
中央値は異常値の影響を受けないため、平均よりもその通りにある住宅の「典型的な」平方フィートをうまく捉えていることがわかります。
まとめ
この記事の主な要点を簡単にまとめます。
- 平均は、一連のデータの平均値を表します。
- 平均値は、データセット内の中心値がどこにあるのかを知ることができるため、重要です。
- 平均値にはデータセット内の各観測値からの情報が含まれるため、平均値も重要です。
- データセットが歪んでいたり、外れ値が含まれている場合、平均値は誤解を招く可能性があります。これらのシナリオでは、中央値によって、データセットの「中心」がどこにあるのかがより正確にわかります。
追加リソース
次のチュートリアルでは、他の記述統計に関する追加情報を提供します。