平均値の標本分布
この記事では、統計における平均値の標本分布がどのようなものであるかについて説明します。また、平均標本分布の公式と段階的に解く練習問題も見つかります。
平均値の標本分布はどうなるでしょうか?
平均値の標本分布(または平均値の標本分布) は、母集団から考えられる各標本の標本平均を計算した結果得られる分布です。つまり、母集団から得られるすべてのサンプルからのサンプル平均のセットが平均の標本分布を形成します。
言い換えれば、母集団から採取できるすべてのサンプルを調査し、各サンプルの平均を計算すると、計算された値のセットがサンプル平均の標本分布を形成します。
統計学では、平均の標本分布は、単一の標本を分析するときに母集団平均の値に近づく確率を計算するために使用されます。
平均値の標本分布の公式
平均値が正規確率分布に従う母集団を仮定すると、
![]()
と標準偏差
![]()
サイズサンプルが抽出されます
![]()
の場合、平均値の標本分布は次の特性を持つ正規分布によって定義されることになります。
![Rendered by QuickLaTeX.com \begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-44571aa7337b095ab9c9fa1f746e93a5_l3.png)
金
![]()
は平均値の標本分布の平均値であり、
![]()
はその標準偏差です。さらに、
![]()
は標本分布の標準誤差です。
注:母集団が正規分布に従わないが、サンプルサイズが大きい場合 (n>30)、中心極限定理によって平均値の標本分布を以前の正規分布に近似することもできます。
したがって、平均値の標本分布は正規分布に従うため、標本平均値に関連する確率を計算する式は次のようになります。

金:
-

はサンプル平均です。
-

これは母集団の平均です。
-

は母集団の標準偏差です。
-

はサンプルサイズです。
-

は、標準正規分布 N(0,1) によって定義される変数です。
平均値の標本分布の実例
平均値の標本分布の定義とそれに関連する式が何であるかを理解した後、概念をよりよく理解するために例を解いてみましょう。
- 大学生の体重は、平均68kg、標準偏差9kgの正規分布に従います。決定した:
- 25 人の生徒からなる無作為サンプルの平均が 66 kg 未満である確率はどれくらいですか?
- それぞれ 25 人の生徒からなる 300 個のサンプルが採取された場合、66 kg 未満の値を持つサンプル平均はいくつありますか?
まず最初に、対応する統計の値を計算する必要があります。このために、上で見た式を適用します。
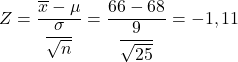
したがって、探している確率は、標準正規分布の左裾の値 Z=-1.11 に対応する確率であり、Z 確率テーブルから簡単に取得できます。したがって、Z テーブルを使用して、問題が尋ねる確率を決定します。
![]()
ランダムサンプルの平均が 66 kg 未満である確率がわかったので、300 個の等しいサンプルを採取して平均 66 kg 未満のサンプル数を知るには、計算された確率に、採取されたサンプルの総数を掛ける必要があります。
![]()
したがって、抽出されたサンプルのうち約 40 個の平均は 66 kg 未満になります。