平均間の差の信頼区間

平均値間の差の信頼区間 (CI) は、一定の信頼レベルで 2 つの母集団平均間の真の差が含まれる可能性が高い値の範囲です。

このチュートリアルでは次について説明します。

• この信頼区間を作成する動機。
• この信頼区間を作成する式。
• この信頼区間を計算する方法の例。
• この信頼区間をどう解釈するか。

平均値間の差異の CI: モチベーション

研究者は多くの場合、2 つの母集団の平均値の差を推定したいと考えます。この差を推定するために、各母集団から無作為にサンプルを収集し、各サンプルの平均を計算します。次に、2 つの平均の差を比較できます。

ただし、標本平均間の差が母集団平均間の真の差に対応するかどうかを確実に知ることはできません。これが、2 つの平均の差の信頼区間を作成できる理由です。これにより、母集団平均間の真の差が含まれる可能性のある値の範囲が得られます。

たとえば、2 つの異なる種のカメの平均体重の差を推定したいとします。各個体群には数千匹のカメが存在するため、各カメを個別に計量して回るのは時間と費用がかかりすぎます。

代わりに、各母集団から 15 匹のカメの 単純なランダム サンプルを取得し、各サンプルの平均体重を使用して、2 つの母集団間の平均体重の本当の違いを推定することができます。

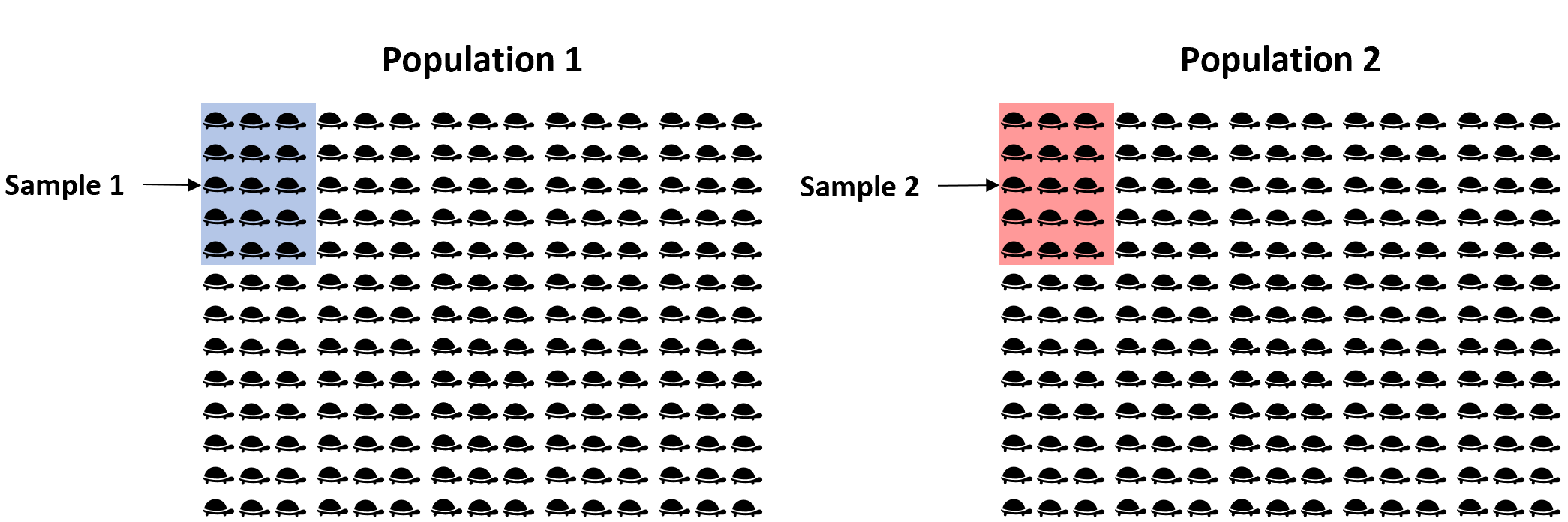
問題は、サンプルがランダムであるため、2 つのサンプル間の平均体重の差が 2 つの母集団間の平均体重の差と正確に一致するという保証がないことです。したがって、この不確実性を捉えるために、2 つの母集団間の平均体重の真の差異が含まれる可能性が高い値の範囲を含む信頼区間を作成できます。

平均間の差の CI:式

次の式を使用して、2 つの平均間の差の信頼区間を計算します。

信頼区間= ( x ₁ – x ₂ ) +/- t*√((s _p ² /n ₁ ) + (s _p ² /n ₂ ))

金：

• x ₁ 、 x ₂ : サンプル 1 の平均、サンプル 2 の平均
• t: 信頼水準と (n ₁ + n ₂ -2) 自由度に基づく t 臨界値
• s _p ² : プールされた分散
• n ₁ 、n ₂ : サンプルサイズ 1、サンプルサイズ 2

金：

• プールされた分散は次のように計算されます。 s _p ² = ((n ₁ -1)s ₁ ² + (n ₂ -1)s ₂ ² ) / (n ₁ +n ₂ -2)
• t 臨界値t は、逆 t 分布計算ツールを使用して見つけることができます。

平均間の差の CI:例

2 つの異なる種のカメの平均体重の差を推定したいとします。したがって、各集団から 15 匹のカメのランダムなサンプルを収集します。各サンプルの概要データは次のとおりです。

サンプル 1:

• x1 = ₃₁₀
• _s1 = 18.5
• n ₁ = 15

サンプル 2:

• x2 ₌ 300
• _s2 = 16.4
• _n2 = 15

母集団平均重みの真の差異に対するさまざまな信頼区間を見つける方法は次のとおりです。

90% 信頼区間:

(310-300) +/- 1.70*√((305.61/15) + (305.61/15)) = [-0.8589, 20.8589]

95% 信頼区間:

(310-300) +/- 2.05*√((305.61/15) + (305.61/15)) = [-3.0757, 23.0757]

99% 信頼区間:

(310-300) +/- 2.76*√((305.61/15) + (305.61/15)) = [-7.6389, 27.6389]

注:これらの信頼区間は、「平均間の差の統計的信頼区間計算ツール」を使用して見つけることもできます。

信頼水準が高くなるほど、信頼区間が広くなることがわかります。区間が広いほど真の母集団平均が含まれる可能性が高く、その区間に真の母集団平均が含まれるという「確信」が高まるため、これは当然のことです。

平均値間の差異に対する CI : 解釈

信頼区間を解釈する方法は次のとおりです。

95% の確率で、信頼区間 [-3.0757, 23.0757] に 2 つのカメ個体群間の平均体重の真の差異が含まれます。

この間隔には値「0」が含まれているため、これら 2 つの個体群のカメ間に平均体重に差がない可能性があることを意味します。言い換えれば、これら 2 つの個体群のカメの間に平均体重に違いがあるとは 95% の信頼を持って言えません。