複数の標準偏差の平均を見つける方法
場合によっては、2 つ以上の標準偏差の平均を求めたい場合があります。
これを行うには、データに応じて次の 2 つの式のいずれかを使用できます。
方法 1: サンプルサイズを均等にする
k 個のグループ間の平均標準偏差を求め、各グループのサンプル サイズが同じである場合は、次の式を使用できます。
平均 SD = √ (s 1 2 + s 2 2 + … + s k 2 ) / k
金:
- sk : k番目のグループの標準偏差
- k : グループの総数
方法 2: サンプルサイズが不均一
k 個のグループ間の平均標準偏差を見つけたい場合で、各グループのサンプル サイズが同じではない場合は、次の式を使用できます。
平均 SD = √ ((n 1 -1)s 1 2 + (n 2 -1)s 2 2 + … + (n k -1)s k 2 ) / (n 1 +n 2 + … + n k – j)
金:
- n k : k番目のグループのサンプルサイズ
- sk : k番目のグループの標準偏差
- k : グループの総数
次の例は、実際に各式を使用する方法を示しています。
方法 1: サンプルサイズが等しい場合の標準偏差の平均を計算する
次の 6 つの販売期間にわたる販売の平均標準偏差を計算するとします。
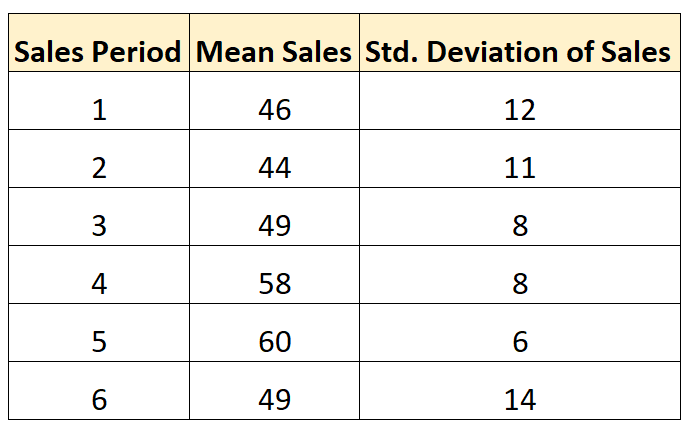
各販売期間中に同じ数の販売取引を行ったと仮定します。次の式を使用して、期間ごとの売上の平均標準偏差を計算できます。
- 平均標準偏差 = √ (s 1 2 + s 2 2 + … + s k 2 ) / k
- 平均標準偏差 = √ (12 2 + 11 2 + 8 2 + 8 2 + 6 2 + 14 2 ) / 6
- 平均標準偏差 = 10.21
期間ごとの売上の平均標準偏差は10.21です。
方法 2: サンプル サイズが等しくない場合の標準偏差の平均化
次の 6 つの販売期間にわたる販売の平均標準偏差を計算するとします。
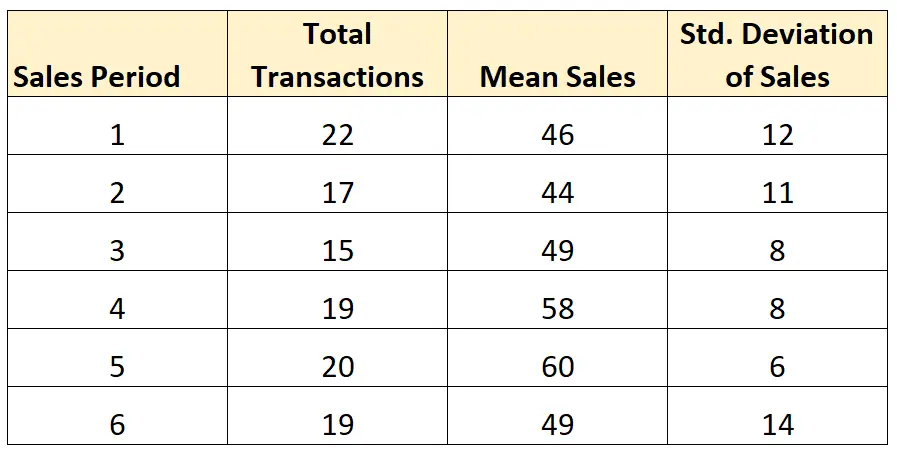
サンプル サイズ (トランザクション総数) は各販売期間で等しくないため、次の式を使用して期間ごとの売上の平均標準偏差を計算します。
- 平均 SD = √ ((n 1 -1)s 1 2 + (n 2 -1)s 2 2 + … + (n k -1)s k 2 ) / (n 1 +n 2 + … + n k – j)
- 平均 SD = √ ((21)12 2 + (16)11 2 + (14)8 2 + (18)8 2 + (19)6 2 + (18)14 2 ) / 106
- 平均SD = 10.29
期間ごとの売上の平均標準偏差は10.29です。
2 つの例の平均標準偏差は非常に似ていることに注意してください。これは、2 番目の例のサンプル サイズ (合計トランザクション) がすべて互いに非常に近かったためです。
平均標準偏差を計算する 2 つの方法は、サンプル サイズがグループ間で大きく異なる場合にのみ大きく異なります。