平均タイプ (統計)

によるベンジャミン・アンダーソン博士 8月 6, 2023 統計 0コメント

ここでは、統計におけるあらゆる種類の平均とは何か、またその計算方法について説明します。ストッキングの種類ごとの公式と例が表示されます。

ただし、平均の種類を理解する前に、統計における平均が何であるかを論理的に知る必要があります。したがって、続行する前に次のリンクを参照することをお勧めします。

統計における平均にはどのような種類がありますか?

統計における平均の種類は次のとおりです。

算術平均
加重平均
幾何学的平均
ルートは正方形を意味します
調和の意味
一般化された平均
一般化された f 平均
トリミングされた手段
四分位間平均
関数の平均

次に、統計におけるあらゆる種類の平均を計算する方法を説明します。最も一般的に使用される平均の 5 つのタイプは、算術平均、加重平均、幾何平均、二次平均、および調和平均です。そこで、これら 5 つの主要なメディアタイプについて詳しく説明します。

算術平均

算術平均は、すべての値を加算し、データポイントの総数で割ることによって計算されます。

したがって、算術平均の式は次のようになります。

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+\dots+x_N}{N}$

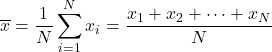
算術平均は、算術平均とも呼ばれます。

算術平均は、おそらく統計で最もよく使用されるタイプの平均です。

このタイプの平均がどのように取得されるかを示す例を確認するために、次のデータの算術平均を計算します。

$4\quad 7\quad 10\quad 1\quad 8\quad9$

算術平均を計算するには、すべての統計データを合計し、データの総数である 6 で割ります。

$\overline{x}=\cfrac{4+7+10+1+8+9}{6}=6,5$

加重平均

加重平均を計算するには、まず各統計データにその重み (または重み) を乗算し、次にすべての積を加算し、最後に重み付き合計をすべての重みの合計で除算する必要があります。

したがって、加重平均の式は次のようになります。

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+\dots x_N\cdot w_N}{w_1+w_2+\dosts +w_N}$

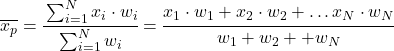
ここで、x _iは統計値、w _{i は}それに対応する重みです。

加重平均を理解するのはさらに難しいため、加重平均の計算方法を段階的に説明する次の例を確認することをお勧めします。

➤参照:加重平均の例

幾何学的平均

一連の統計データの幾何平均は、すべての値の積の n 乗根に等しくなります。

このタイプの平均は、ビジネスファイナンスで収益率、平均パーセンテージ、複利を計算するために使用されます。

このタイプのストレージの計算式は非常に複雑です。実際、すべての統計セットの幾何平均を計算することはできませんが、この種の平均を決定できない場合もあります。このため、次のリンクで説明されているすべての例外を参照することをお勧めします。

➤参照:幾何平均の公式

ルートは正方形を意味します

二乗平均平方根は、データの二乗の算術平均の平方根に等しい。

したがって、平均二乗公式は次のようになります。

$\displaystyle RMS=\displaystyle\sqrt{\frac{1}{N}\sum_{i=1}^N x_i^2}=\sqrt{\frac{x_1^2+x_2^2+\dots + x_N^2}{N}\vphantom{\sum_{i=1}^N x_i^2}}}$

このタイプの平均は、二乗平均平方根、二乗平均平方根、またはRMSとも呼ばれます。

3 次平均も存在しますが、これは非常に特殊な場合に使用されることを指摘しておきます。

二乗平均には長所と短所があり、たとえば、各データを二乗することですべての値が正になるため、統計変数が正と負の値をとる場合に特に便利です。次のリンクをクリックすると、このメディアタイプのその他の機能を確認できます。

➤参照:二乗平均平方根の長所と短所

調和の意味

調和平均は、統計データの総数を各値の逆数の合計で割ることによって計算されます。

$\displaystyle H=\frac{N}{\displaystyle\sum_{i=1}^N\frac{1}{x_i}}=\frac{N}{\displaystyle\frac{1}{x_1}+\frac{1}{x_2}+\dots+\frac{1}{x_N}}$

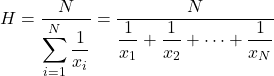
調和平均は、平均速度、時間を計算したり、電子計算を行ったりするために使用されます。この特性により、調和平均は、価格平均やパーセンテージの計算によく使用される他のタイプの平均と区別されます。

このタイプの平均の計算例は、次のページで確認できます。

➤参照:高調波の意味の例

他の種類のストッキング

このセクションでは、他のタイプのストッキングの公式を見ていきます。広く使用されているものではないため、それぞれのタイプについて詳しくは説明しませんが、他のタイプのストッキングがあることを知っておくと良いでしょう。

一般化された平均は、上記の平均タイプを組み合わせたもので、次の式を使用して計算されます。

$\displaystyle\overline{x}(m) = \left ( \frac{1}{N}\cdot\sum_{i=1}^N{x_i^m} \right ) ^{1/m}$

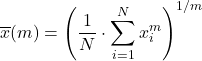
f を単調関数とすると、一般化された f 平均は次のように定義されます。

$\displaystyle\overline{x} = f^{-1}\left({\frac{1}{N}\cdot\sum_{i=1}^N{f(x_i)}}\right)$

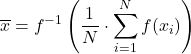
トリミング平均には、サンプルの上端と下端の観測値のパーセンテージを差し引いた後、算術平均を計算することが含まれます。同じ割合が両端で拒否される必要があります。

四分位間平均(四分位間平均とも呼ばれる) を計算するには、最初に第 1 四分位数と第 4 四分位数のデータが破棄され、次にサンプルの第 2 四分位数と第 3 四分位数の算術平均のみが計算されます。したがって、このタイプの平均の式は次のようになります。

$\displaystyle\overline{x}={2 \over n} \sum_{i=\frac{n}{4}+1}^{\frac{3n}{4}}{x_i}$

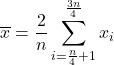
最後に、関数の平均を求めることもできます。閉区間 [a,b] 上の連続関数の平均値は、次の式を使用して計算されます。

$\displaystyle\overline{f}=\frac{1}{b-a} \int_a^b f(t) dt$

サンプルと母集団の平均

最後に、混同されやすい 2 種類の平均である標本平均と母集団平均の違いについて説明します。

サンプル平均は、統計サンプルの値に対して計算された平均です。つまり、変数のすべての値の一部に対して計算されます。

母集団平均は、統計上の母集団、つまり変数のすべての値にわたって計算された平均です。したがって、母集団の平均は変数の数学的期待値と一致します。

十分に大量のデータがわかっている場合、標本平均は母集団の平均と実質的に等しいと考えることができます。しかし、実際には分布のすべての値がわかっていることはほとんどないため、母集団の平均値を取得するのは非常に困難です。

著者について

ベンジャミン・アンダーソン博士

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る