平行形状の信頼性とは何ですか? (定義&例)
統計学では、並列形式の信頼性は、テストの 2 つの同等な形式間の相関を測定します。
並列形式の信頼性を計算するプロセスは次のとおりです。
ステップ 1: テストを半分に分割します。
たとえば、100 問のテストを、50 問を含むテスト A と、同じく 50 問を含むテスト B にランダムに分割します。
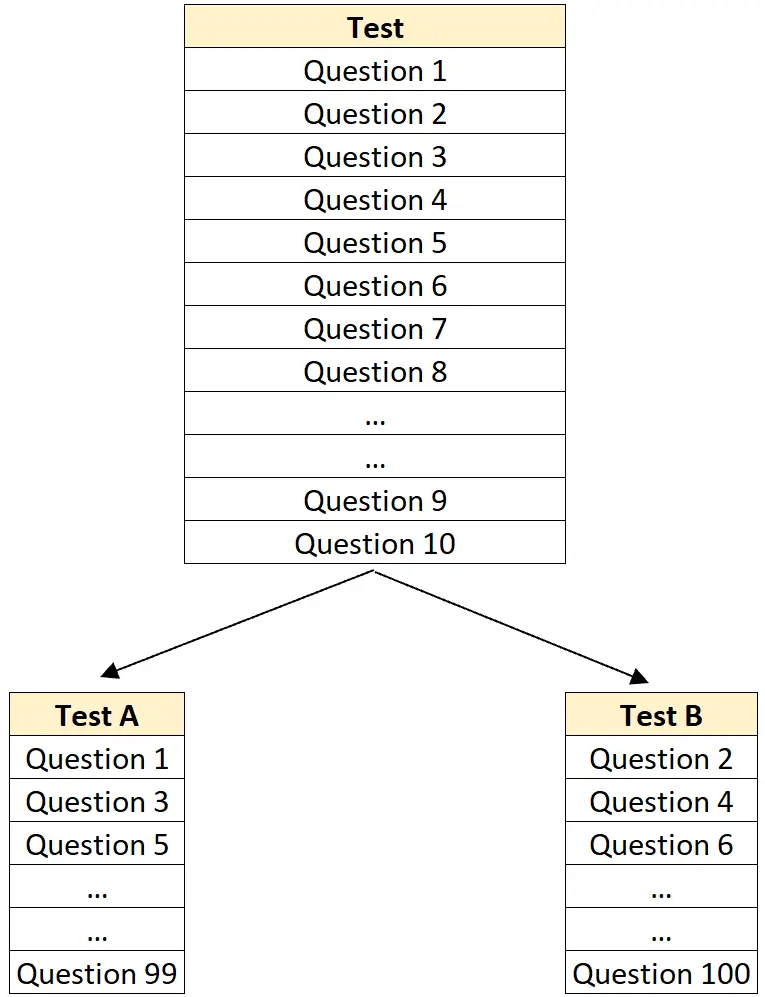
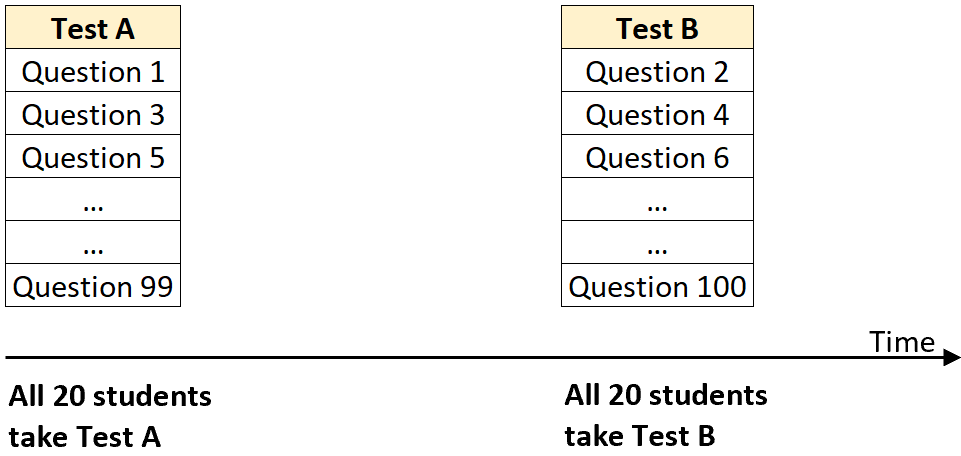
ステップ 2: 前半をすべての生徒に実施し、次に後半をすべての生徒に実施します。
たとえば、特定のクラスの 20 人の生徒全員にテスト A を実施し、得点を記録します。次に、おそらく 1 か月後、同じ 20 人の生徒にテスト B を実施し、そのテストのスコアも記録します。
ステップ 3: 2 つのテストのテストスコア間の相関を計算します。
2 つのテストのスコア間の相関関係を計算します。スコア間の相関が高い場合、テストは並列形式の信頼性があると言われます。
並列フォームの信頼性をいつ使用するか
並列形式の信頼性は、教授が学生に事前にテスト問題にアクセスさせたくない場合に、学術的な環境でよく使用されます。
たとえば、教授が学期の初めにすべての学生にテスト A を配布し、学期の終わりに同じテスト A を配布した場合、学生は最初のテストの問題と回答を暗記するだけで済みます。
ただし、学期の終わりに別の B テスト (できれば同じ難易度) を配布することで、教授は学生が以前に問題を見たことがないことを確認しながら、学生の知識を評価することができます。
平行形式の信頼性の潜在的な欠点
並列形式の信頼性には、2 つの潜在的な欠点があります。
1. 多くの質問が必要です。
並列形式の信頼性は、相関関係について計算される数値の信頼性がより高くなるため、質問数が多いテスト (例: 100 問) に最適です。
2. 2 つの半分が実際に平行であるという保証はありません。
テストをランダムに 2 つの部分に分割した場合、その 2 つの部分が実際に並行するか、難易度が「等しい」という保証はありません。これは、単に一方が他方より難しいという理由だけで、2 つのテストのスコアが異なる可能性があることを意味します。
並列フォームの信頼性と分割半分の信頼性
並列フォームの信頼性は2 分の 1 の信頼性と似ていますが、わずかな違いがあります。
信頼性は 2 つに分けられます。
これには、テストを 2 つの半分に分割し、それぞれの半分を同じ生徒グループに実施することが含まれます。学生がテストを受ける順序は関係ありません。
この方法の利点は、内部の一貫性を測定できることです。理想的には、テストのすべての部分が測定対象に等しく寄与していることを示すため、半分間の相関が高くなることを望みます。
並列形式の信頼性:
これには、テストを 2 つの半分に分割し (それらを「A」と「B」と呼びます)、それぞれの半分を同じ生徒グループに実施することが含まれます。
ただし、すべての生徒が最初に「A」テストを受け、次に「B」テストを受けることが重要です。そのため、「A」テストの答えを知っていても、後で「A」テストを受ける生徒には何のメリットもありません。 B」。