Excelで幾何分布を使用する方法

幾何分布は、一連のベルヌーイ試行で最初の成功を経験する前に、一定回数の失敗を経験する確率を表します。

ベルヌーイ試行は、「成功」または「失敗」の 2 つの結果しか考えられない実験であり、実験が実行されるたびに成功の確率は同じです。

ベルヌーイのエッセイの例としては、コイントスがあります。コインは 2 つの表にのみ着地できます (表を「ヒット」、裏を「失敗」と呼びます)。コインが公正であると仮定すると、各フリップでの成功確率は 0.5 です。

確率変数X が幾何分布に従う場合、最初の成功を経験する前にk回の失敗を経験する確率は、次の式で求められます。

P(X=k) = (1-p) ^kp

金：

• k:最初の成功までの失敗回数
• p:各試行の成功確率

次の例は、Excel で幾何分布に関連する確率を計算する方法を示しています。

例 1: コインを投げる

コインを投げて、最終的にコインが表になるまでにちょうど 3 回の「ミス」が必要になる確率を知りたいとします。

この確率を計算するには次の式を使用します。

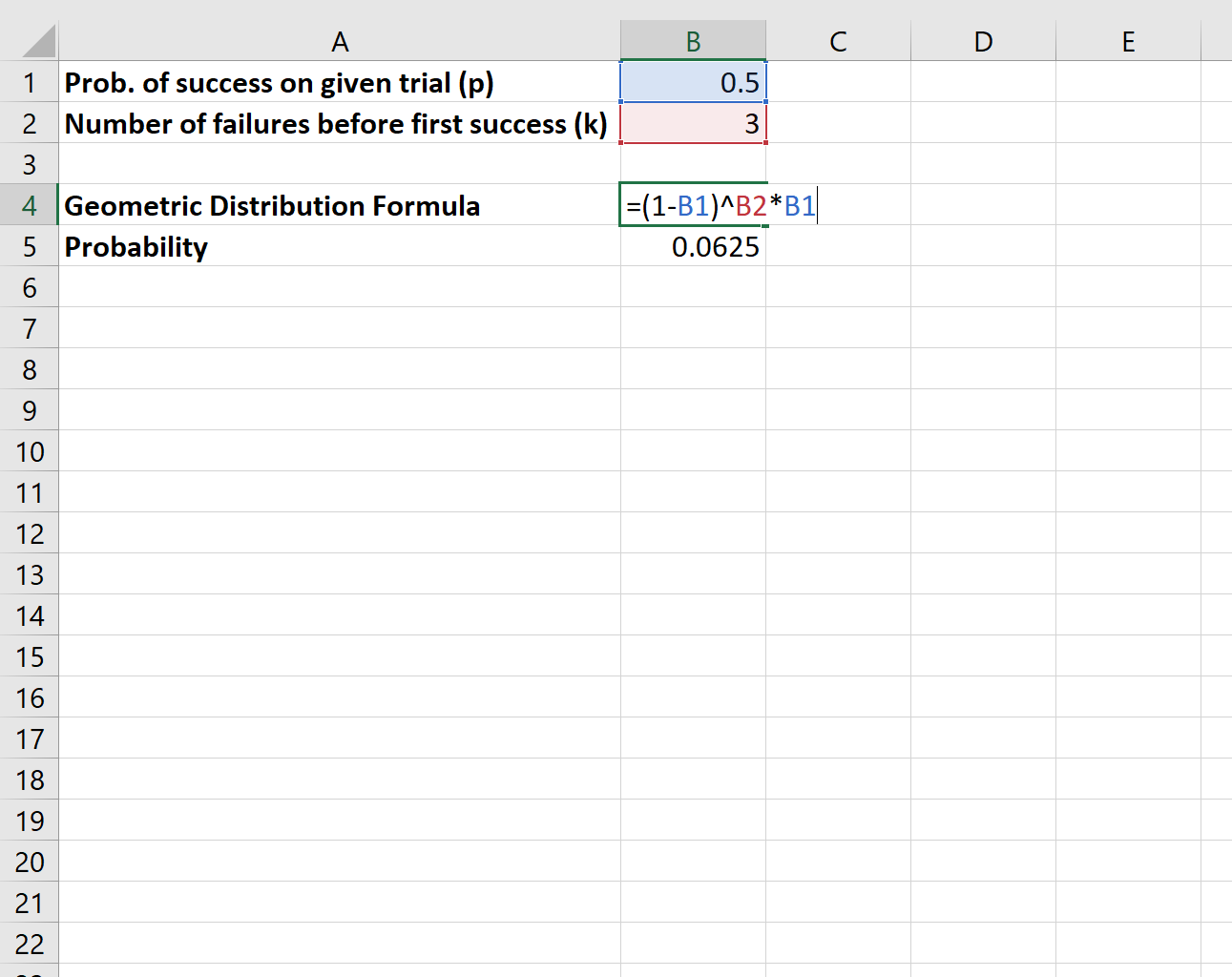
最終的にコインが表になるまでに 3 回の「ミス」が発生する確率は0.0625です。

例 2: フリースロー射撃

あるバスケットボール選手がフリースローの 60% を成功させたとします。プレーヤーが最終的にフリースローを 1 本決めるまでに 4 本のフリースローを失敗する確率はどれくらいですか?

この確率を計算するには次の式を使用します。

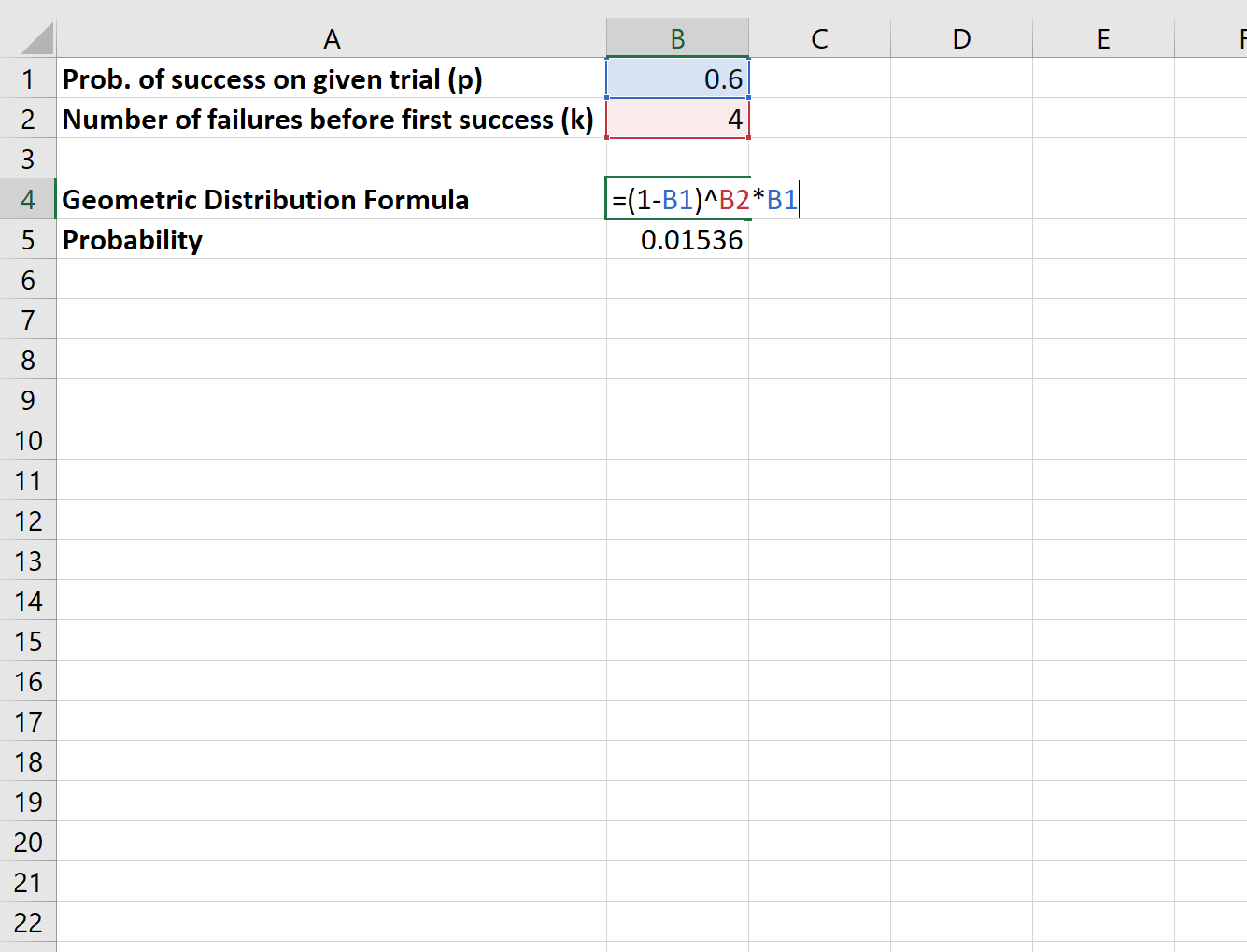
プレーヤーが最終的に 1 本を決めるまでに 4 本のフリースローを失敗する確率は0.01536です。

例 3: 法律の支持

研究者が図書館の外で待っていて、人々に特定の法律を支持するかどうか尋ねたとします。特定の人が法則を支持する確率は p = 0.2 です。研究者が話しかけた 4 人目の人がその法律を最初に支持する確率はどれくらいですか?

この確率を計算するには次の式を使用します。

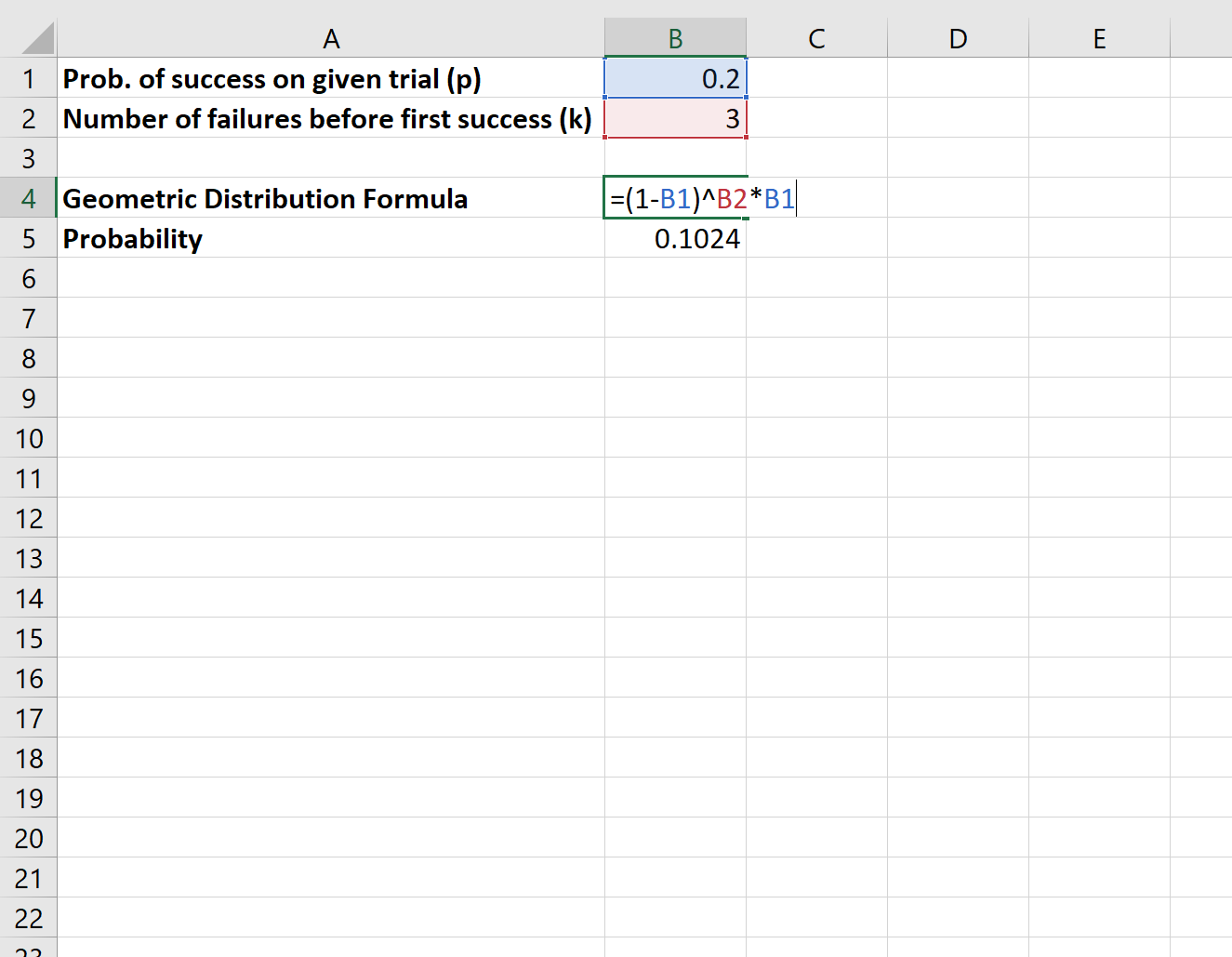
研究者が話しかけた 4 人目が最初にこの法則を支持する確率は0.1024です。

追加リソース

幾何分布の概要
幾何分布計算機
幾何学的分布の 5 つの具体例