度数表

この記事では、統計における度数表とは何かについて説明します。したがって、度数表の作成方法や度数表の例がわかり、さらに、解決された演習で練習することができます。

度数表とは何ですか?

統計学における度数表とは、一連のデータがさまざまなカテゴリに編成され、あらゆる種類のサンプリング周波数が表示される表です。

具体的には、度数テーブルには、絶対度数、累積絶対度数、相対度数、累積相対度数が含まれる。

度数表の特徴の 1 つは、量的変数と質的変数の統計サンプルを要約するために使用されることです。

度数表の作り方

度数表を作成する手順は次のとおりです。

1. データをさまざまなカテゴリに整理し、各行がカテゴリに対応するテーブルを作成します。
2. 度数表の 2 列目にある各カテゴリの絶対度数を計算します。
3. 度数表の 3 列目にある各カテゴリの累積絶対度数を計算します。
4. 度数表の 4 列目の各カテゴリの相対度数を計算します。
5. 度数表の 5 列目にある各カテゴリの累積相対度数を計算します。
6. オプションで、相対度数と累積相対度数をパーセンテージとして計算する 2 つの列を追加できます。このためには、両方の列に 100 を掛けるだけで済みます。

変数が連続の場合、度数表のカテゴリは数値ではなく間隔になることに注意してください。度数表がどのように作成されるかを理解できるように、ここでは段階的に解決する 2 つの例を示します。1 つ目ではデータが分離され、2 つ目ではデータが間隔にグループ化されます。

度数表の例

頻度表の定義とその構築方法に関する理論を考慮して、このセクションでは例を段階的に解決します。

• 30人学級における統計科目の成績は以下の通りです。データセットの頻度表を作成します。

すべての数値は整数のみであるため、これは離散変数です。したがって、データを間隔にグループ化する必要はありません。

したがって、それぞれの異なる値が行となるテーブルを構築する必要があります。さらに、各値の絶対頻度を見つける必要があります。これを行うには、単にデータ サンプル内に値が出現する回数を数えます。

すべての絶対周波数の合計がデータの総数に等しいことに注意してください。このルールが守られない場合は、特定の情報を提供するのを忘れたことを意味します。

絶対周波数がわかったので、累積絶対周波数を計算する必要があります。この計算には 2 つのオプションがあります。値の絶対頻度と最小値のすべての絶対頻度を加算するか、その逆に、値の絶対頻度と前の値の累積絶対頻度を加算します。

最後の値の累積絶対頻度は常にデータの総数に対応するため、このトリックを使用して計算が正しいことを確認できます。

次に、相対頻度を決定する必要があります。相対頻度は、絶対頻度をデータ ポイントの総数 (30) で割ることによって計算されます。

すべての相対度数の合計は常に 1 に等しいことに注意してください。そうでない場合は、度数表の計算の一部が間違っていることを意味します。

最後に、累積された相対周波数を抽出するだけで十分です。これを行うには、問題の値の相対度数に以前のすべての相対度数を加えたもの、または同じことになりますが、以前に累積された相対度数を加算する必要があります。

つまり、問題のあるデータのすべての頻度を含む頻度表は次のとおりです。

グループ化されたデータの度数表

間隔 にグループ化されたデータの度数表を作成するには、最初にデータセットを異なる間隔にグループ化する必要があるという点が唯一の違いですが、残りの計算は度数表の場合と同じ方法で実行されます。データをグループ化せずに頻度を調べます。

例として、グループ化されたデータの頻度表の構築に関する問題を以下で解決します。

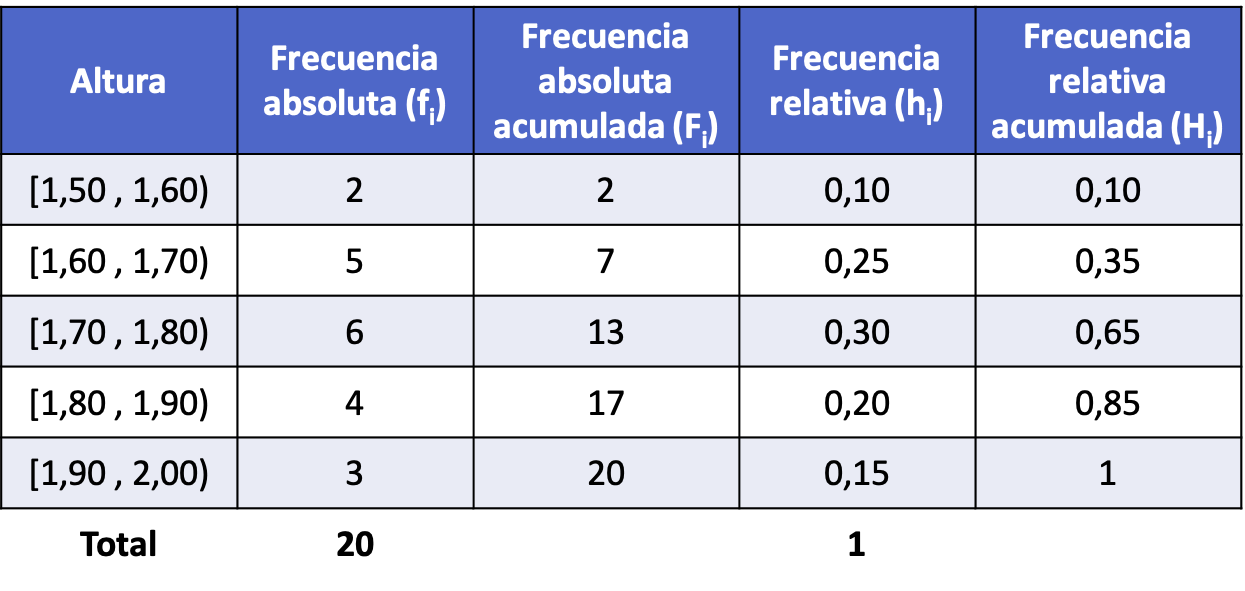
• 20名の身長を測定したところ、以下の結果が得られました。データを間隔に分割する度数表を準備します。

このサンプルのデータは、数値が 10 進数であるため、任意の値を取り得るため、連続分布に従います。したがって、データを間隔にグループ化する度数表を作成します。

サンプルの間隔を作成するにはいくつかの数学的規則がありますが、この場合は単純に 10 分の 10 の幅で間隔を作成します。

したがって、各間隔のすべてのタイプの頻度を計算した後 (手順は前の例と同じです)、データが間隔にグループ化された頻度テーブルは次のようになります。

度数表の演習を解決しました

演習 1

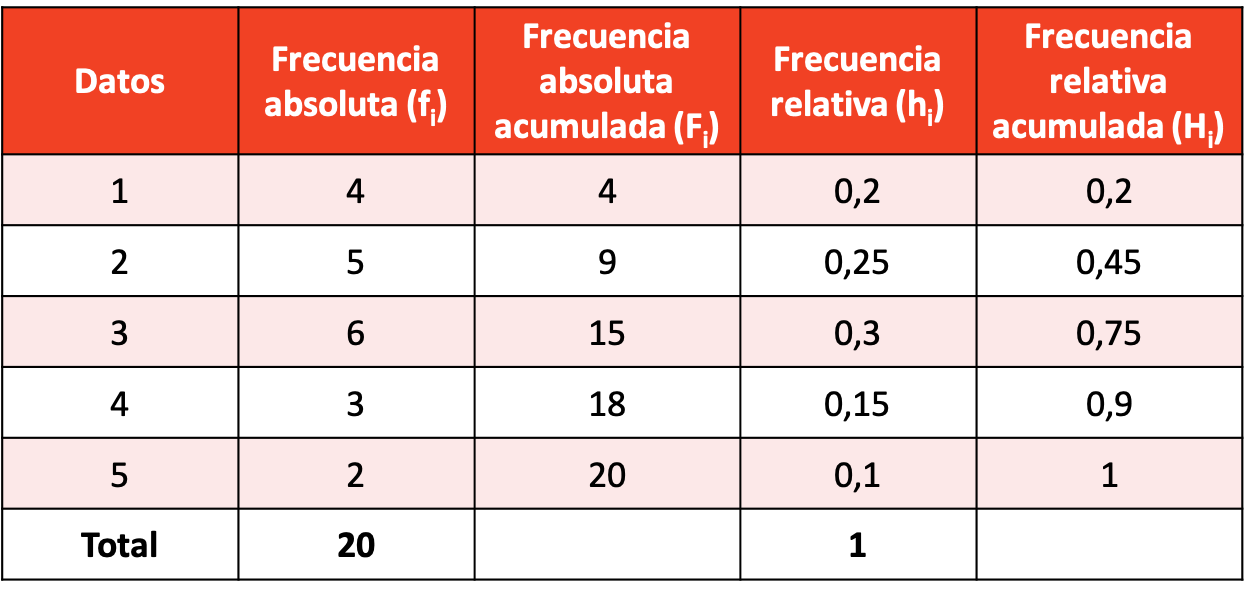
20人に月に何回映画館に行くかを尋ねた結果は次のとおりです。

得られたサンプル データを使用して度数表を作成します。

すべてのタイプの周波数の計算を含む周波数テーブルは次のとおりです。

演習 2

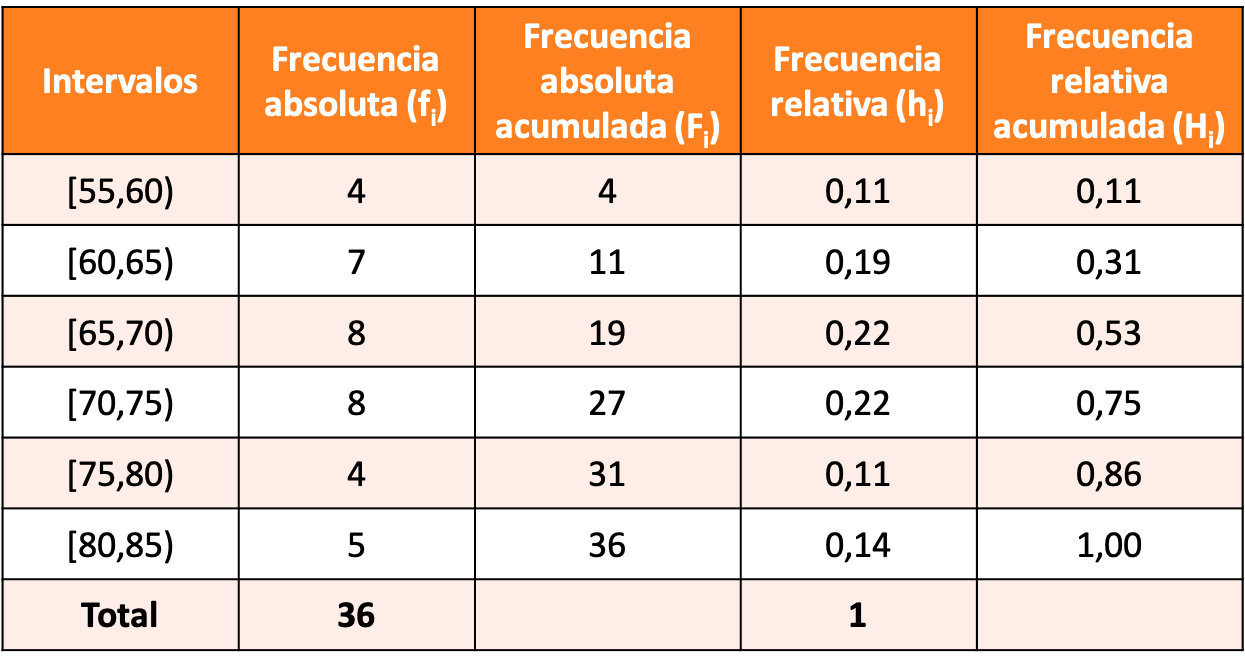
従業員数 36 人の会社の従業員の体重について統計調査を実行したいと考えています。作業員の体重をキログラムで表すと次のようになります。

5 単位の間隔を作成し、最初の間隔を [55,60) としてグループ化したデータを含む度数表を作成します。

この演習の解決策は、次の頻度表です。