カイ二乗検定を手動で実行する方法 (ステップバイステップ)

カイ二乗適合度検定は、カテゴリ変数が仮説分布に従うかどうかを判断するために使用されます。

次の段階的な例は、カイ二乗適合度検定を手動で実行する方法を示しています。

手動によるカイ二乗適合度テスト

あるサイコロが正しいと信じているとします。言い換えれば、特定のロールでサイコロが 1、2、3、4、5、または 6 に出る確率は同じであると考えられます。

これをテストするために、60 回投げて、毎回着地する数を記録します。結果は次のとおりです。

• 1 ：8倍
• 2：12回
• 3：18回
• 4 ：9倍
• 5 ：7倍
• 6 ：6回

次の手順に従って、カイ二乗適合度検定を実行して、サイコロが公平かどうかを判断します。

ステップ 1: 帰無仮説と対立仮説を定義する

• H ₀ (null): サイコロが各数字に着目する確率は同じです。
• H ₁ (代替): サイコロが各数字に当たる確率は同じではありません。

ステップ 2: 観測された周波数と期待される周波数を計算する

次に、サイコロの各数字の観測頻度と期待頻度の表を作成しましょう。

注: サイコロが公平であると考える場合、それは、サイコロが各数字に同じ回数、この場合は 10 回ずつ出ると期待していることを意味します。

ステップ 3: 検定統計量を計算する

カイ二乗検定統計量 X ²は次のように計算されます。

• X ² = Σ(OE) ² / E

次の表は、この検定統計量の計算方法を示しています。

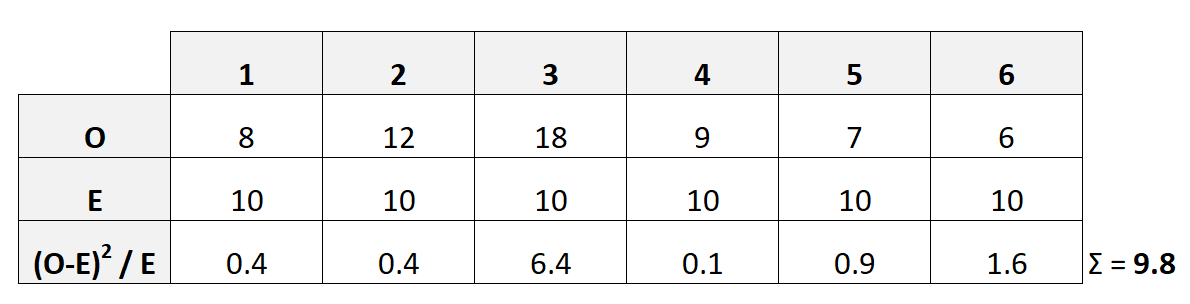
この場合、X ^{2 は}9.8であることがわかります。

ステップ 4: 臨界値を見つける

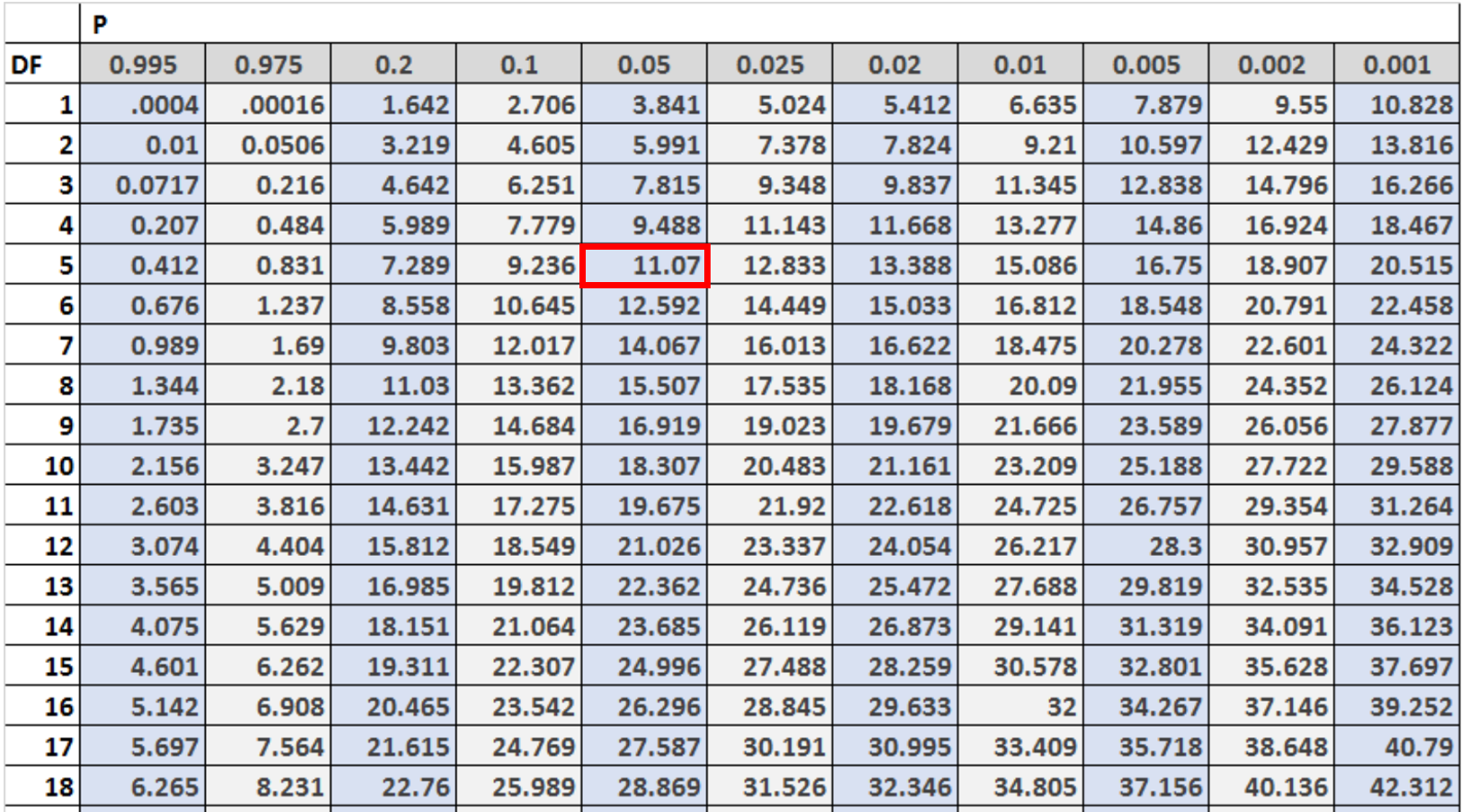
次に、α = 0.05および df = (#categories – 1) に対応するカイ二乗分布表の臨界値を見つける必要があります。

この場合、カテゴリは 6 つあるため、 df = 6 – 1 = 5を使用します。

臨界値は11.07であることがわかります。

ステップ 5: 帰無仮説を棄却する、または棄却に失敗する

検定統計量が臨界値より小さいため、帰無仮説を棄却できません。これは、サイコロが不公平であると言える十分な証拠がないことを意味します。

追加リソース

次のリソースは、カイ 2 乗適合度検定に関する追加情報を提供します。

カイ二乗適合度検定の概要
R でカイ二乗適合度検定を実行する方法
カイ二乗適合度検定計算ツール