推定値の標準誤差はどれくらいですか? (定義&例)
推定値の標準誤差は、回帰モデルによる予測の精度を測定する方法です。
σ estは次のように計算されます。
σは= √ Σ(y – ŷ) 2 /n
金:
- y:観測値
- ŷ:予測値
- n:観測値の総数
推定値の標準誤差は、回帰モデルがデータセットにどの程度適合しているかを知ることができます。特に:
- 値が小さいほど、適合度が高くなります。
- 値が大きいほど、適合性は悪くなります。
推定値の標準誤差が小さい回帰モデルの場合、データ ポイントは推定された回帰直線の周囲に密集します。
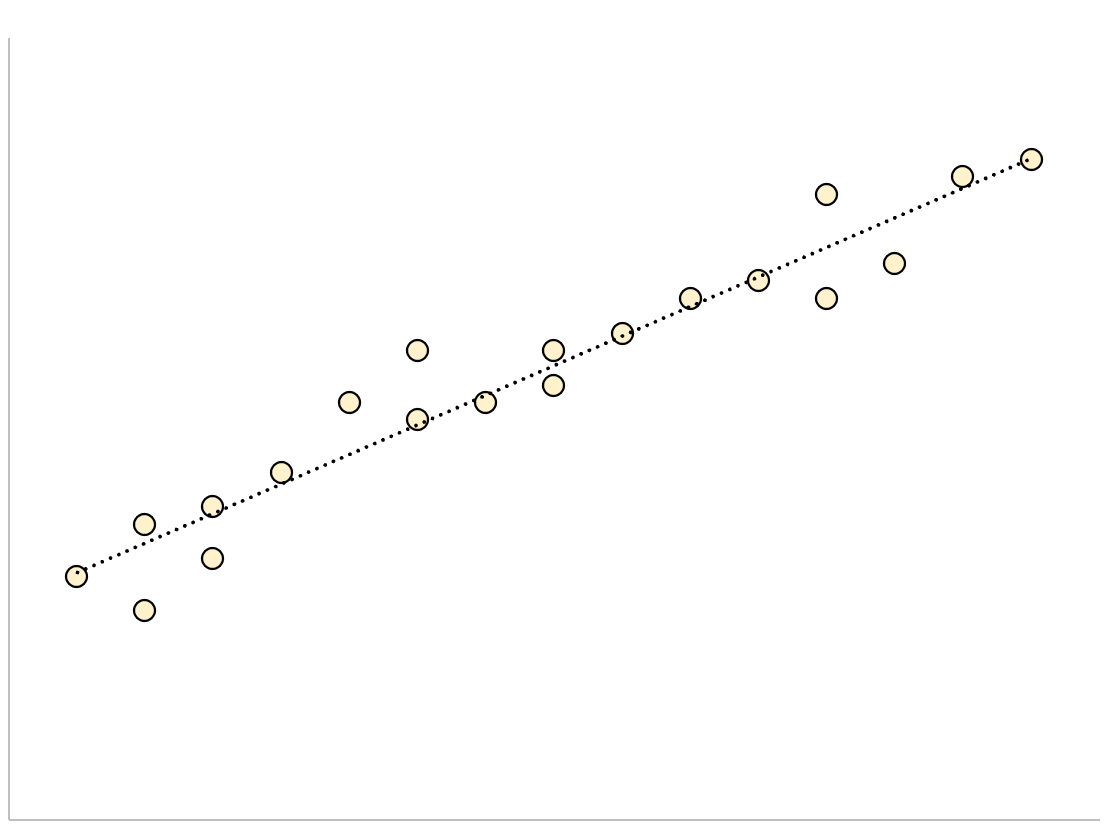
逆に、推定の標準誤差が大きい回帰モデルの場合、データ ポイントは回帰直線の周りにさらに緩やかに分散します。
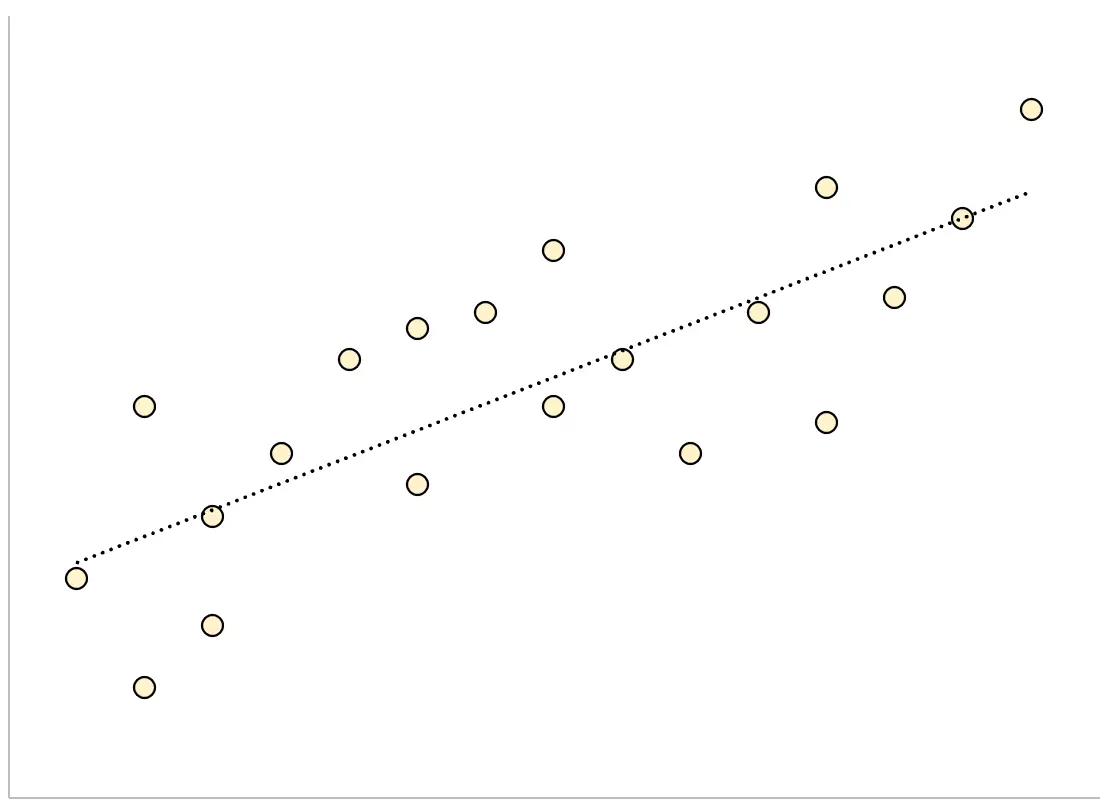
次の例は、Excel で回帰モデルの推定値の標準誤差を計算して解釈する方法を示しています。
例: Excel での推定の標準誤差
Excel で回帰モデルの推定値の標準誤差を計算するには、次の手順を使用します。
ステップ 1: データを入力する
まず、データセット値を入力します。
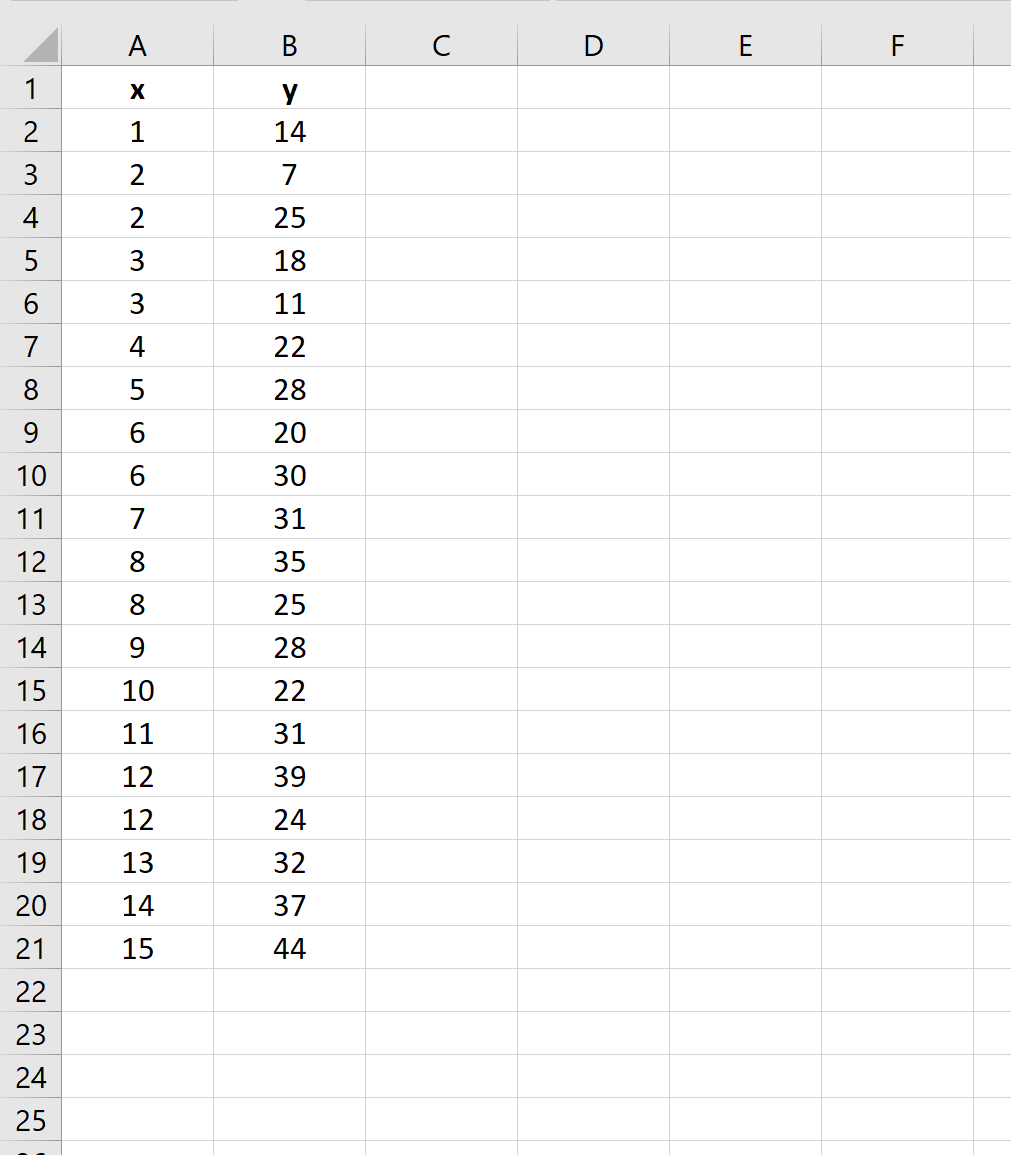
ステップ 2: 線形回帰を実行する
次に、上部のリボンに沿って[データ]タブをクリックします。次に、 「分析」グループの「データ分析」オプションをクリックします。

このオプションが表示されない場合は、まずAnalysis ToolPak をロードする必要があります。
表示される新しいウィンドウで、 「回帰」をクリックし、 「OK」をクリックします。
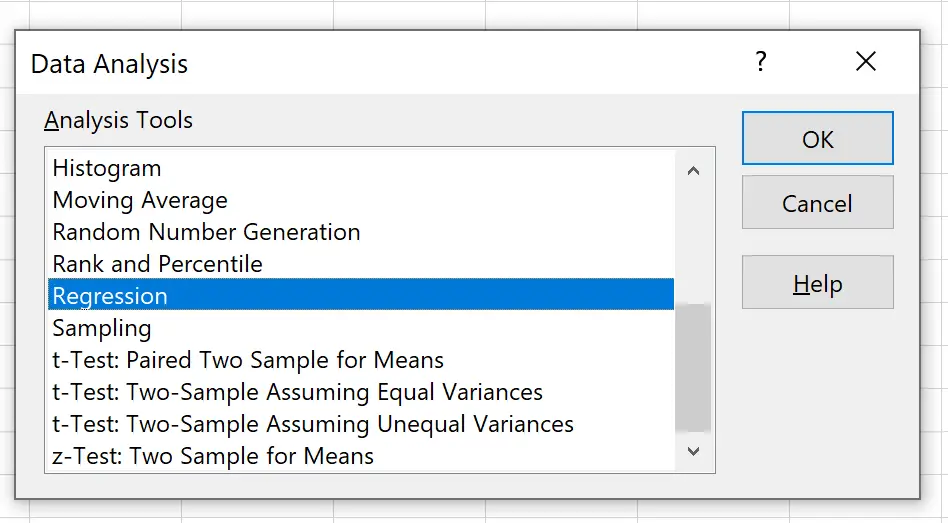
表示される新しいウィンドウで、次の情報を入力します。
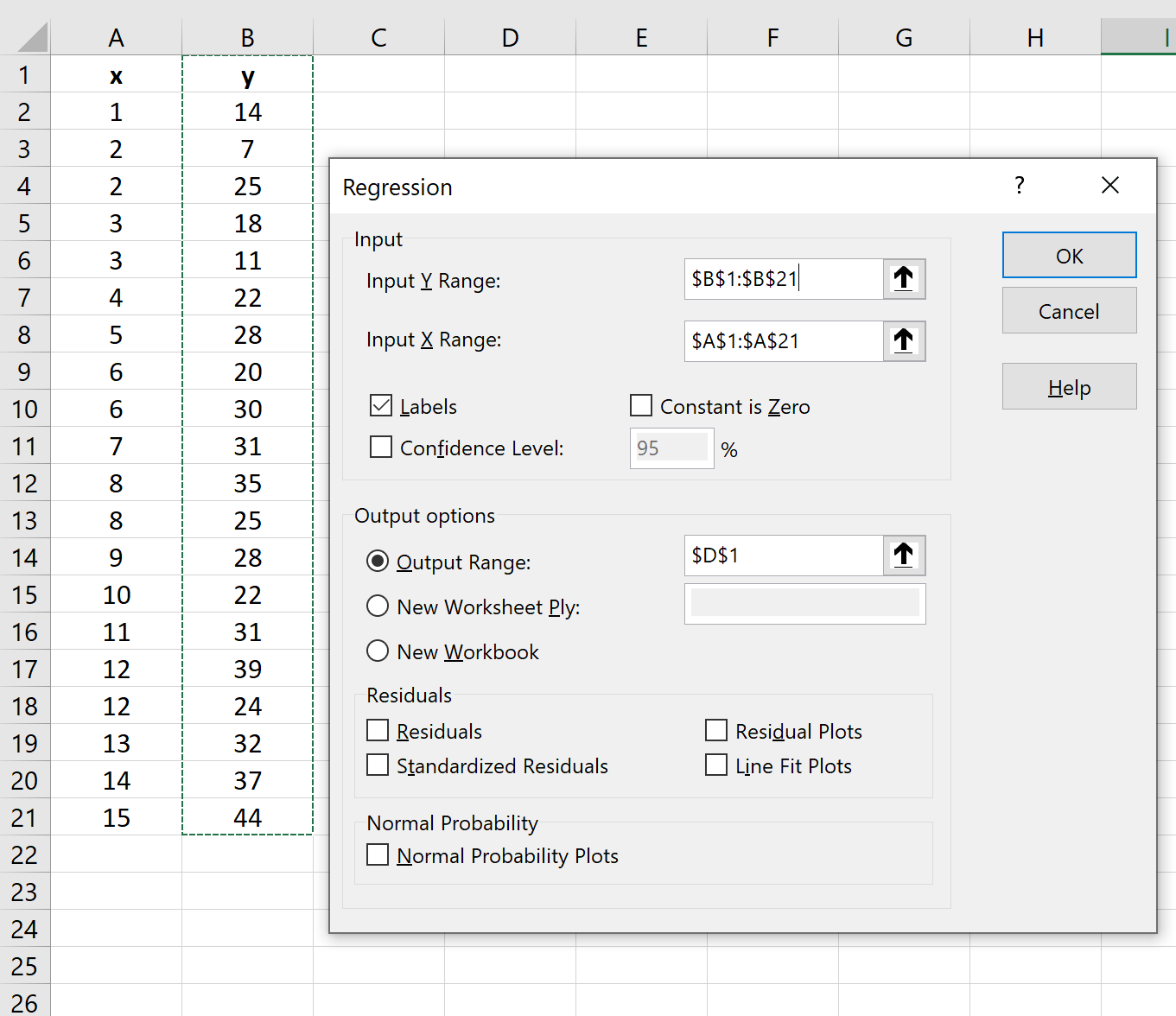
[OK]をクリックすると、回帰結果が表示されます。
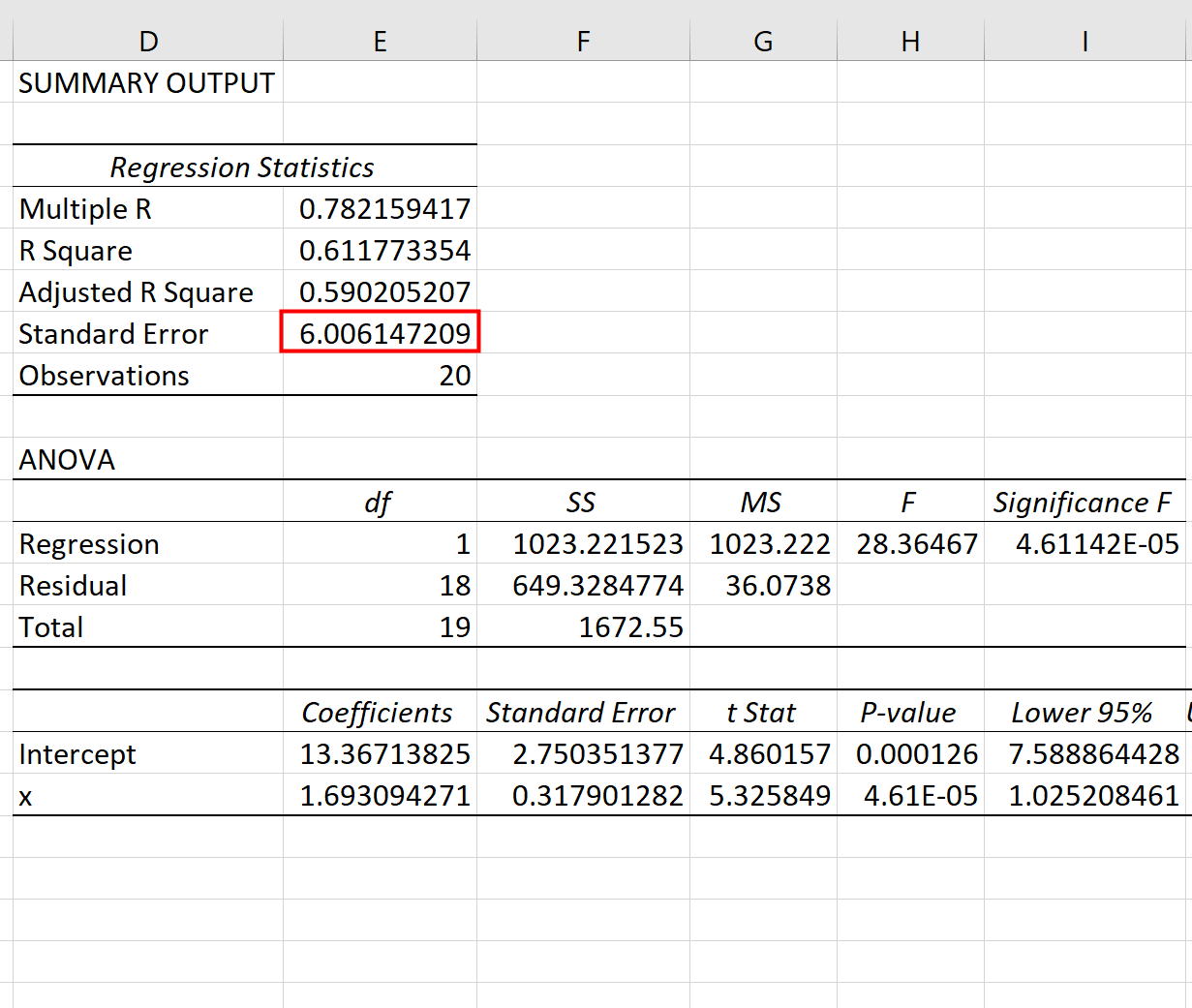
回帰表の係数を使用して、推定された回帰式を構築できます。
ŷ = 13.367 + 1.693(x)
そして、この回帰モデルの推定値の標準誤差は6.006であることがわかります。簡単に言うと、平均データ ポイントが回帰直線から6.006単位離れていることがわかります。
推定回帰式と推定値の標準誤差を使用して、特定のデータ ポイントの予測値の 95% 信頼区間を構築できます。
たとえば、x が 10 に等しいとします。推定された回帰式を使用して、y が次と等しいと予測します。
ŷ = 13.367 + 1.693*(10) = 30.297
そして、次の式を使用して、この推定値の 95% 信頼区間を取得できます。
- 95% CI = [ŷ – 1.96*σは、ŷ + 1.96*σは]
この例では、95% 信頼区間は次のように計算されます。
- 95% CI = [ŷ – 1.96*σは、ŷ + 1.96*σは]
- 95% CI = [30.297 – 1.96*6.006、30.297 + 1.96*6.006]
- 95% CI = [18,525, 42,069]