操作変数: 定義と例
多くの場合、統計では、ある変数が別の変数に及ぼす影響を推定しようとします。たとえば、次のことを知りたいかもしれません。
- 勉強に費やした時間は試験の得点にどのように影響しますか?
- 特定の薬は血圧にどのような影響を及ぼしますか?
- ストレスは心拍数にどのような影響を与えるのでしょうか?
各シナリオで、予測変数が応答変数に影響を与えるかどうかを理解したいと考えています。ただし、多くの場合、2 つの変数間の関係に影響を与える他の変数が存在します。
たとえば、特定の薬剤を予測変数として使用し、血圧を応答変数として使用するとします。私たちは血圧に対する薬物の影響のみに興味があります。
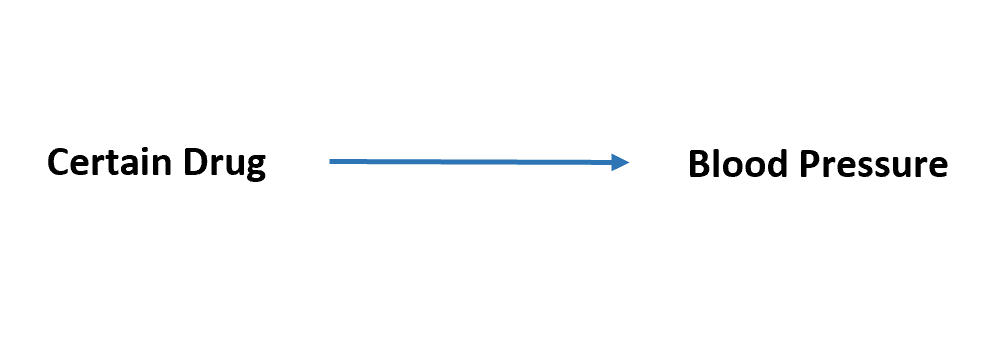
ただし、運動に費やした時間、一般的な食事、ストレスレベルなどの他の変数も血圧に影響します。
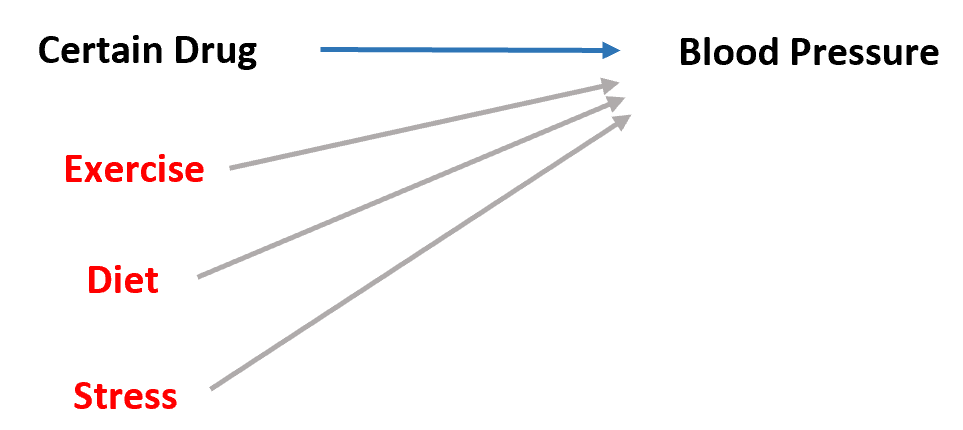
したがって、薬物を予測変数として使用し、血圧を応答変数として使用して単純な線形回帰を実行した場合、 回帰係数が血圧に対する薬物の影響を正確に捉えるかどうかは保証できません。食事、ストレスなど)も影響を与える可能性があります。
この問題を回避する考えられる方法の 1 つは、操作変数を使用することです。
操作変数とは何ですか?
操作変数は、回帰分析に導入される 3 番目の変数で、予測変数とは相関しますが、応答変数とは相関しません。この変数を使用すると、予測変数が応答変数に与える真の因果効果を推定することが可能になります。
たとえば、特定の薬物の血圧に対する効果を推定したいとします。

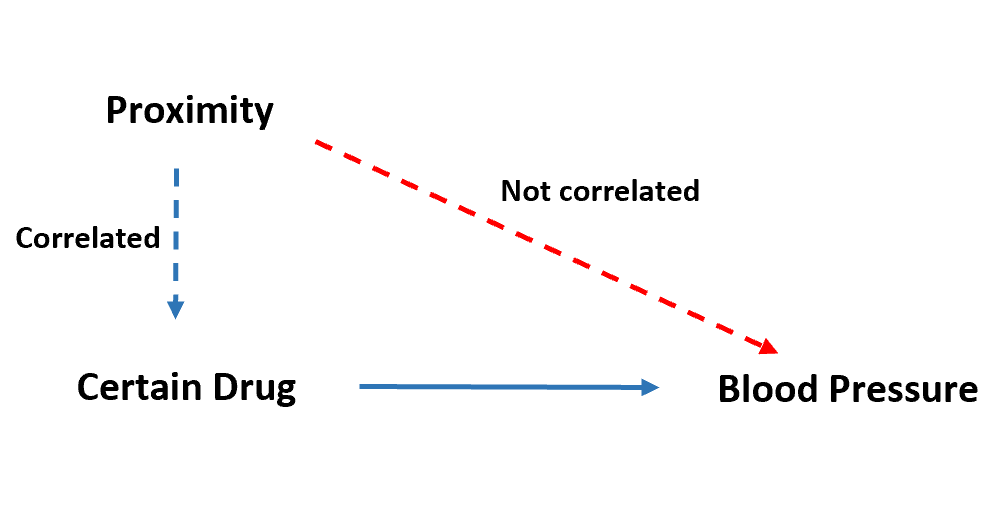
この回帰分析で使用できる操作変数の例は、個人の薬局への近さです。
個人は薬局の近くに住んでいない場合、そもそも薬を入手できないため、この「近接性」変数は、個人が問題の薬を服用しているかどうかと非常に相関している可能性があります。

ただし、「近接」変数は血圧と相関関係があってはなりません。血圧との唯一の関連性は、予測変数によるものです。
実際に操作変数を使用する方法は、操作変数回帰(二段階最小二乗回帰とも呼ばれます) を実行することです。
操作変数回帰
操作変数回帰 (または 2 段階最小二乗回帰) は、次のアプローチを使用して、応答変数に対する予測変数の影響を推定します。
ステップ 1: 操作変数を予測変数として使用して回帰モデルを近似します。
この具体的な例では、まず次の回帰モデルを当てはめます。
特定の薬剤 = B 0 + B 1 (近接性)
その後、特定の薬物 (cd) の予測値が残ります。これを cd hat と呼びます。
ステップ 2: cd hatの予測値を使用して 2 番目の回帰モデルを近似します。
次に、次の回帰モデルを当てはめます。
血圧 = B 0 + B 1 (cdハット)
cd hatの回帰係数が統計的に有意であることが判明した場合、血圧に対する薬剤の因果関係があると言えます。
このようなことが言える理由は、CD Hatを作成するために「近接性」という用語を使用しただけであり、近接性が血圧と相関するはずがなく、第 2 段階の回帰における有意な相関は特定の薬剤に起因する可能性があることがわかっているからです。
操作変数の使用上の注意
操作変数は、次の基準を満たす場合にのみ使用する必要があります。
- 予測変数と強い相関があります。
- 応答変数とは相関しません。
- これは、モデルから除外された他の変数とは相関しません (たとえば、近接性は運動、食事、またはストレスと相関しません)。
操作変数がこの基準を満たさない場合は、信頼性の低い偏った結果が生成される可能性があるため、回帰モデルでは使用しないでください。