散布図

この記事では、散布図とは何かについて説明します。したがって、点群が何に使用されるか、点群を作成する方法、点群を解釈する方法、および点群の例を理解できます。

点群とは何ですか?

散布図、または散布図 は、2 つの変数のデータセットが 2 つのデカルト座標軸上にグラフ化される統計図の一種です。

したがって、散布図は 2 つの統計変数間の関係を分析するために使用されます。

散布図には、相関図や散布図など、いくつかの異なる名前があります。

散布図は、パレート図、特性要因図、フローチャートなどと同様に、品質管理の基本ツールの 1 つとみなされていることに注意してください。

散布図の作り方

散布図を作成するには、次の手順に従う必要があります。

1. 分析したいサンプルから統計データを収集します。散布図を作成するには、少なくとも 2 つの量的変数が必要であることに注意してください。
2. 散布図の 2 つの軸をプロットします。
3. グラフ化する 2 つの統計変数を決定します。
4. グラフの各軸のスケールを調整します。これを行うには、まず各変数の最小値と最大値を見つけ、これらの値に基づいて各軸をスケールすることをお勧めします。
5. 散布図上のデータの各ペアを点で表します。
6. 得られた散布図を分析して解釈します。

散布図の例

散布図の定義とその作成理論を見た後、このセクションでは例としてこのタイプの図を示します。

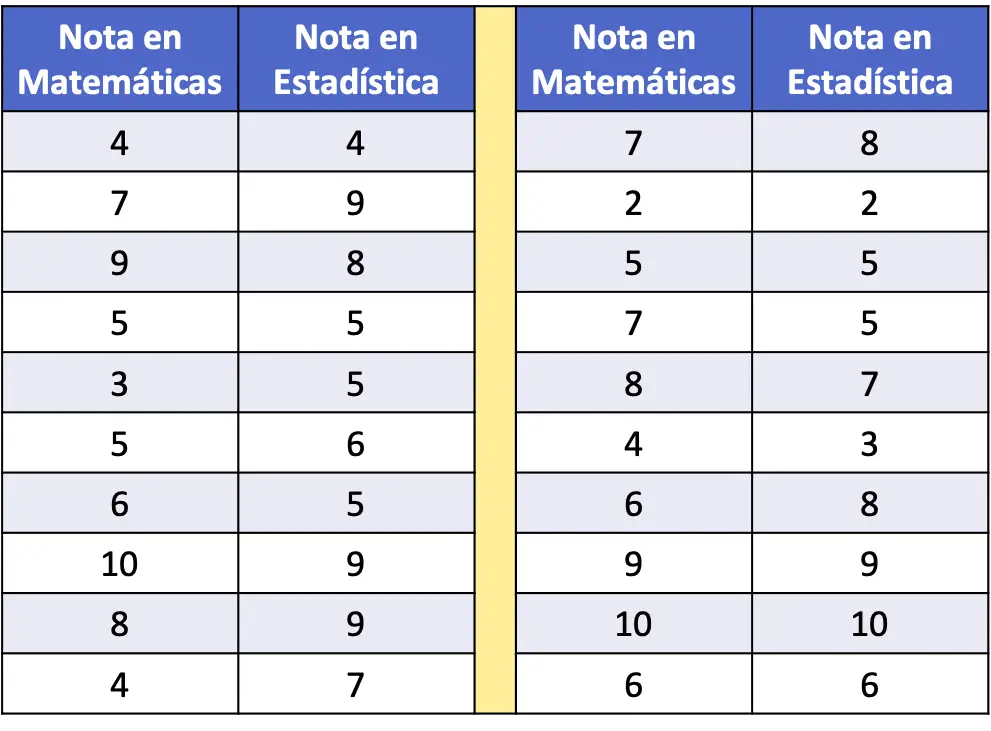
• 次の度数表では、20 人の生徒のサンプルの数学と統計のスコアがデータとして収集されました。データセットを散布図にプロットして分析します。

データ系列を散布図で表すには、2 つの軸をプロットし、それらを校正して、データの各ペアについてグラフ上に点をプロットするだけです。グラフ上の点は、その各値に対応する仮想線の交点に配置されることに注意してください。

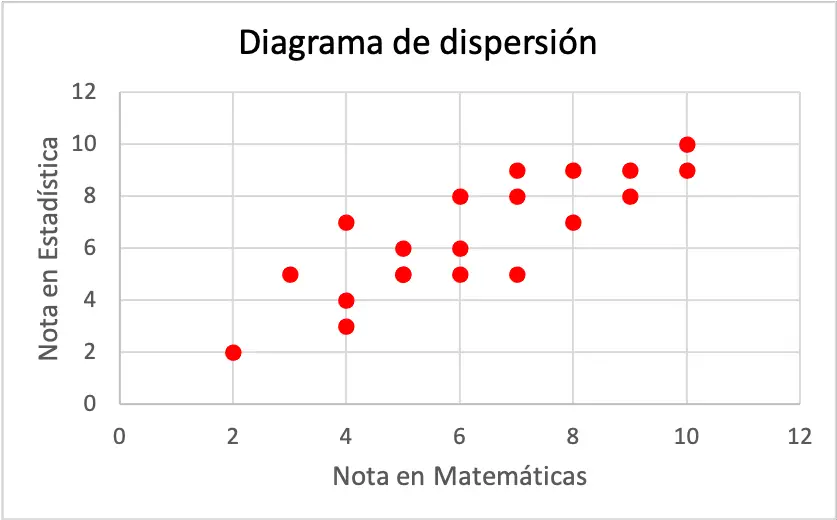
散布図の各軸は変数を表します。より正確には、横軸は数学で得られる成績に属し、一方、縦軸は統計で得られる成績に対応します。

散布図からわかるように、一方の変数が増加するともう一方の変数も増加するため、2 つの変数には正の相関関係があります。したがって、生徒が数学でより良い成績をとれば、統計でもより良い成績を得る可能性が高く、その逆も同様であると結論付けられます。

ただし、前述の結論は、一方の変数がもう一方の変数の原因であるという意味ではありません。数学で良い成績をとったからといって、何もせずに自動的に統計で良い成績が保証されるわけではなく、むしろ両方の科目を勉強する必要があるからです。次のセクションでは、この概念について詳しく説明します。

散布図と相関関係

散布図から、2 つの変数間の相関のタイプを識別することができます。

• 直接相関 (または正の相関) : 一方の変数が増加すると、他方の変数も増加します。
• 逆相関 (または負の相関) : 一方の変数が増加すると、他方の変数は減少し、逆も同様で、一方の変数が減少すると、他方の変数は増加します。
• ゼロ相関 (相関なし) : 2 つの変数間に関係がありません。

同様に、2 つの変数間の相関が直接的であるか逆相関であるかにかかわらず、2 つの変数間の関係の強さまたは弱さに基づいて相関関係を分類することもできます。

• 強い相関関係: 2 つの変数は密接に関連しています。点は点群上にまとめられます。これにより、変数間の関係を識別しやすくなります。
• 低相関: 2 つの変数間に関係は存在しますが、特定するのは困難です。点群上では点は互いに遠く離れています。

一方、相関関係は数式を使用して数値的に計算することもでき、2 つの異なる変数がどの程度密接に関連しているかを数学的に知ることができます。どのように機能するかを確認するには、次のリンクをクリックしてください。

2 つの変数間に相関関係がある場合でも、それはそれらの間に因果関係があることを意味するわけではないことに留意してください。つまり、2 つの変数間の相関関係は、一方の変数の変化がもう一方の変数の変化の原因であることを意味するわけではありません。変数。

したがって、前のセクションの散布図のように、数学の成績と統計の成績の間には正の相関関係がありますが、数学で良い成績を取得しても、統計で良い成績を取得することを意味するわけではありません。数学だけを勉強すると必ず失敗します。統計では。したがって、2 つの変数には関連性がありますが、原因と結果はありません。

さらに詳しく知りたい場合は、次の投稿を続けてください。

点群の長所と短所

散布図の特性により、このタイプの統計グラフには長所と短所があります。

アドバンテージ：

• 散布図上で一連のデータを表すのは非常に簡単です。
• 散布図を使用すると、2 つの変数間の関係を視覚的に分析できるため、結論を導きやすくなります。
• 散布図は、予備的なデータ探索として詳細な統計調査にも使用できます。

短所:

• このような種類の図は、質的変数を表すのには役に立ちません。
• 散布図を解釈すると、2 つの変数間の原因と結果について誤った結論が得られる可能性があります。
• 散布図では、3 つ以上の変数間の関係を分析できません。