曲線回帰とは何ですか? (定義と例)
曲線回帰は、直線ではなく曲線を近似しようとする回帰モデルに付けられた名前です。
曲線回帰モデルの一般的な例は次のとおりです。
二次回帰:予測変数と応答変数の間に二次関係が存在する場合に使用されます。グラフにすると、このタイプの関係は散布図上の「U」または反転した「U」のように見えます。
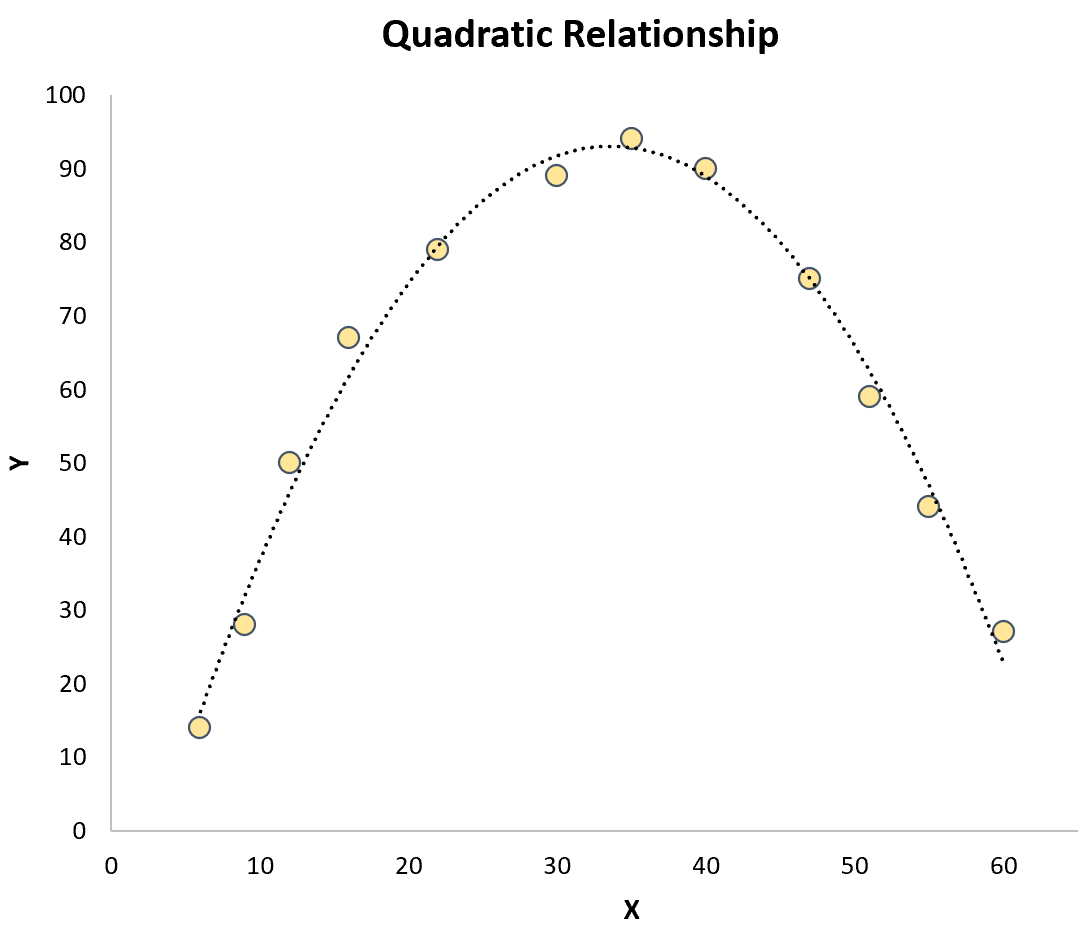
3次回帰:予測変数と応答変数の間に3次関係が存在する場合に使用されます。このタイプの関係をグラフ化すると、散布図上に 2 つの異なる曲線が表示されます。
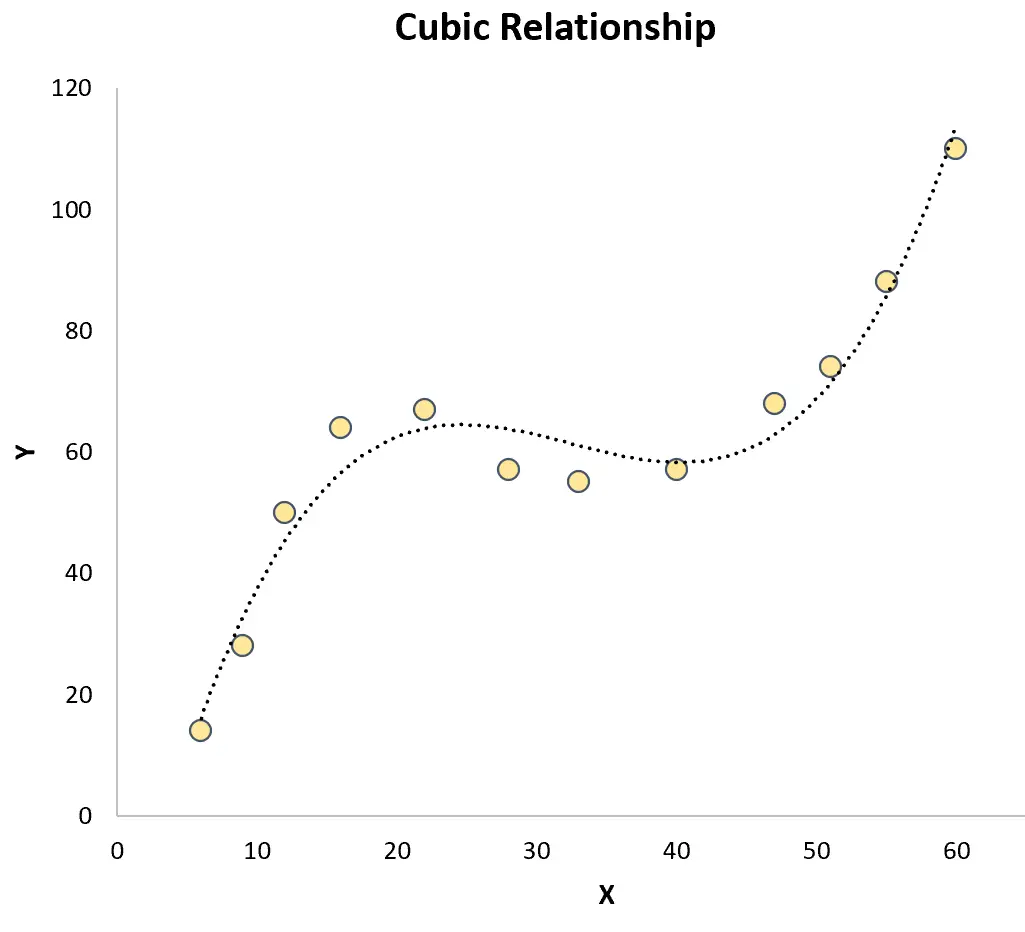
これらはどちらも、予測変数と応答変数の関係が線形である単純な線形回帰とは対照的です。
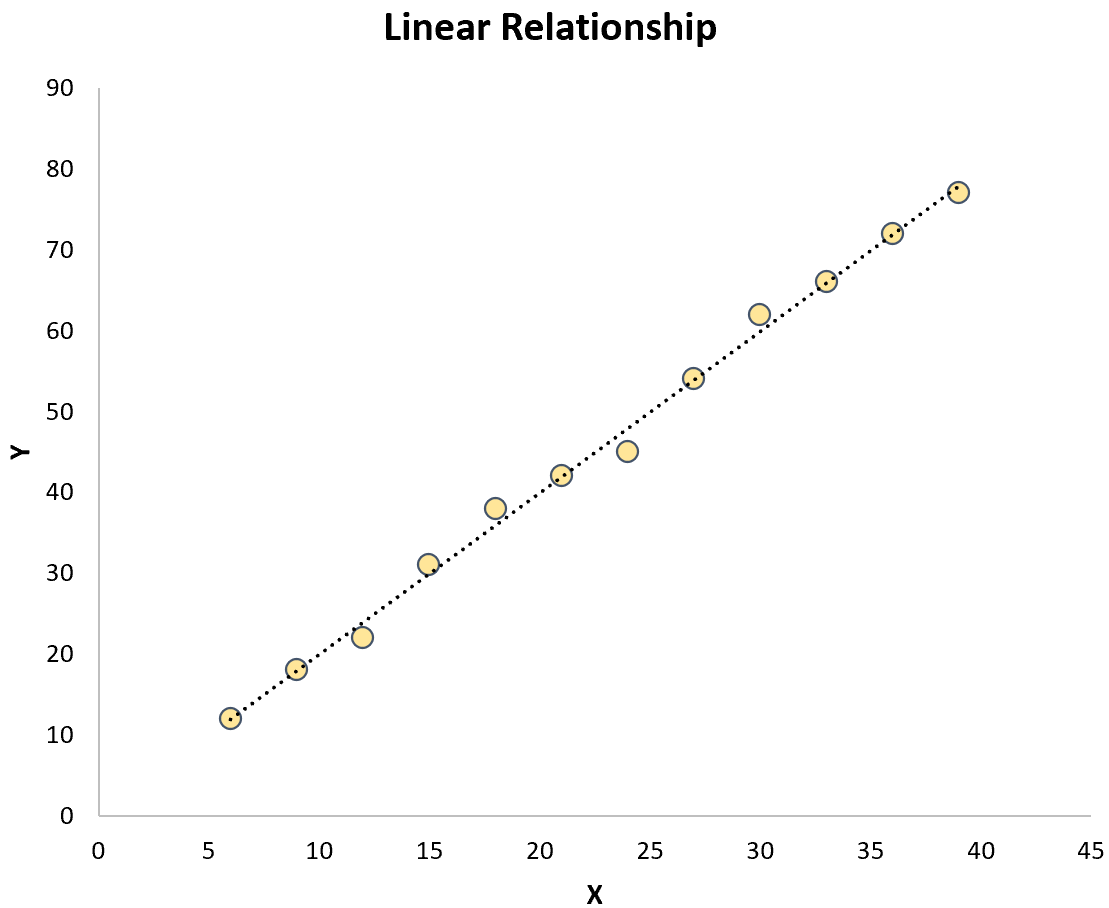
曲線回帰モデルの公式
単純な線形回帰モデルは、次の式を使用して一連のデータを近似しようとします。
ŷ = β 0 + β 1 x
金:
- ŷ:応答変数
- β 0 、β 1 :回帰係数
- x:予測変数
対照的に、二次回帰モデルでは次の式が使用されます。
ŷ = β 0 + β 1 x + β 2 x 2
また、 3 次回帰モデルでは次の式が使用されます。
ŷ = β 0 + β 1 x + β 2 x 2 + β 3 x 3
指数を含む回帰モデルに与えられるより一般的な名前は多項式回帰であり、次の式を使用します。
ŷ = β 0 + β 1 x + β 2 x 2 + … + β k x k
kの値は多項式の次数を示します。次数には任意の正の数値を指定できますが、実際には、3 または 4 を超える次数で多項式回帰モデルを近似することはほとんどありません。
回帰モデル式で指数を使用することにより、多項式回帰モデルは直線ではなく曲線をデータセットに適合させることができます。
曲線回帰を使用する場合
曲線回帰を使用する必要があるかどうかを知る最も簡単な方法は、予測変数と応答変数の散布図を作成することです。
散布図が 2 つの変数間の線形関係を示している場合は、単純な線形回帰がおそらく適切です。
ただし、散布図が予測変数と応答変数の間に 2 次、3 次、またはその他の曲線パターンを示している場合は、おそらく曲線回帰を使用する方が適切です。
また、単純な線形回帰モデルと曲線回帰モデルを近似し、各モデルの近似 R 二乗値を比較して、どのモデルがデータに最適に適合するかを判断することもできます。
調整済み R 二乗は、モデル内の予測子変数の数に応じて調整された、応答変数の分散が予測子変数によってどの程度説明できるかを示すため便利です。
一般に、調整された R 二乗値が最も高いモデルは、データセットによりよく適合します。
追加リソース
次のチュートリアルでは、さまざまな統計ソフトウェアで多項式回帰を実行する方法について説明します。
多項式回帰の概要
Excel で多項式回帰を実行する方法
Python で多項式回帰を実行する方法
R で多項式回帰を実行する方法