標準偏差が重要なのはなぜですか? (説明+例)

標準偏差は、サンプル内の値の分布を測定するために使用されます。

次の式を使用して、特定のサンプルの標準偏差を計算できます。

√ Σ(x _i – x _bar ) ² / (n-1)

金：

• Σ： 「和」を意味する記号
• x _i :サンプルの^{i 番目}の値
• x _bar :サンプルの平均値
• n:サンプルサイズ

標準偏差値が高いほど、サンプル内での値の分散が大きくなります。逆に、標準偏差値が低いほど、値はより密接にクラスター化されます。

学生がよく尋ねる質問は、「標準偏差はなぜ重要ですか?」です。

答え:標準偏差は、特定のデータセット内の値の分布を示すため重要です。

データセットを分析するときはいつでも、次の指標を見つけたいと考えます。

• データセットの中心。 「中心」を測定する最も一般的な方法は、平均と中央値を使用することです。
• データセット内の値の分布。スプレッドを測定する最も一般的な方法は、標準偏差を使用することです。

中心がどこにあり、値の分布がどのようになっているかを知ることで、任意のデータセット内の値の分布をよく理解できます。

次の例は、実際における標準偏差の重要性を示しています。

例 1: 給与の分配

会社 A の平均給与が 80,000 ドル、標準偏差が 20,000 ドルであると仮定します。標準偏差が非常に大きいため、給与にばらつきがあるため、この会社で働いていれば年収8万ドル近くをもらえるという保証はありません。

逆に、B 社の平均給与も 80,000 ドルであるが、標準偏差はわずか 4,000 ドルであるとします。この標準偏差は非常に小さいため、給与の変動はほとんどなく、80,000 ドル近くが支払われることは確実です。

これら 2 つの企業の給与分布を視覚化する箱ひげ図を作成すると、次のようになります。

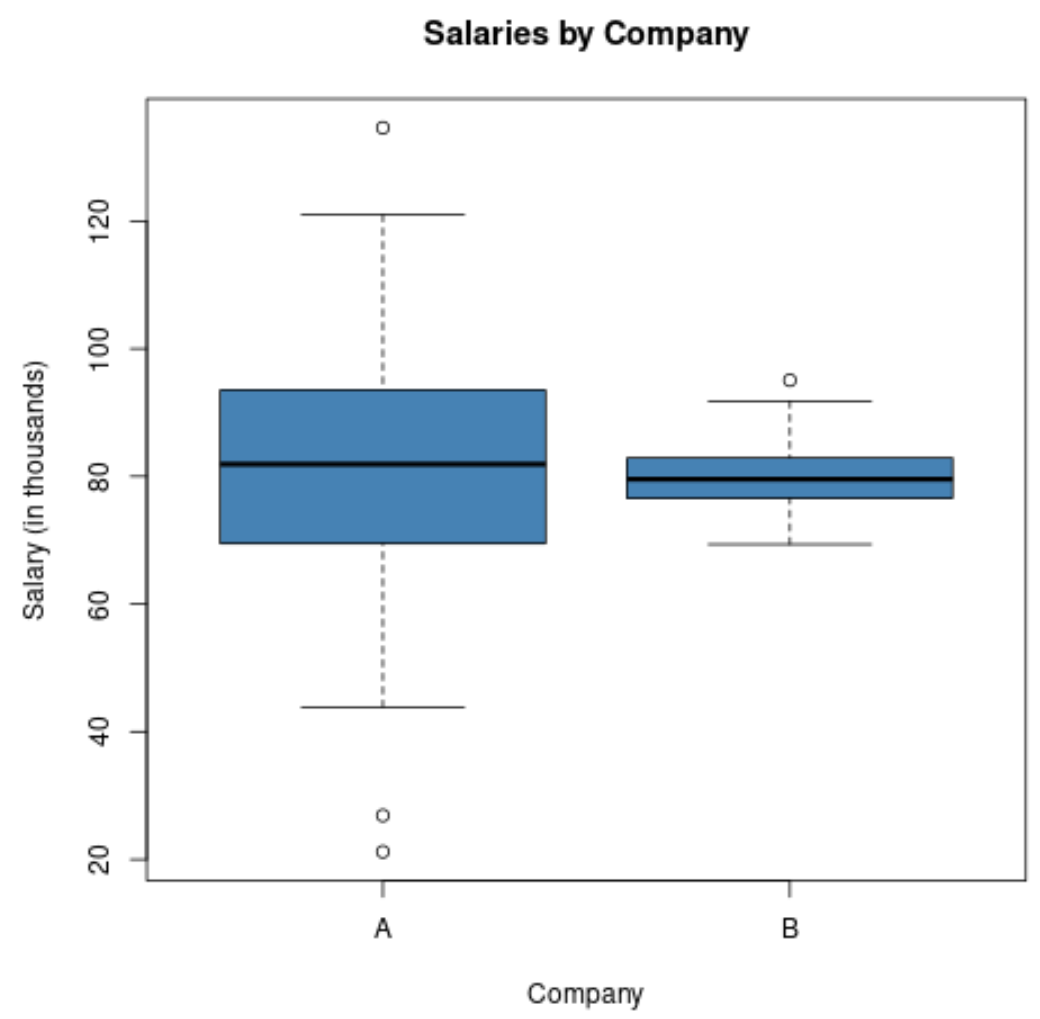
賃金の標準偏差がはるかに大きいため、会社 A の箱ひげ図の長さが長くなっていることに注意してください。

両社の平均給与は同じですが、給与の差はA社の方がはるかに大きいです。

例 2: 住宅価格の分布

近隣 A の平均住宅価格が 250,000 ドル、標準偏差が 50,000 ドルであると仮定します。標準偏差が非常に大きいため、住宅価格には 250,000 ドルよりもはるかに高いものもあれば、はるかに低いものもあるということになります。この地域のどの住宅を見ても、価格が平均に近いという保証はありません。

逆に、近隣 B の平均住宅価格も 250,000 ドルであるが、標準偏差はわずか 10,000 ドルであるとします。この標準偏差は非常に小さいため、近隣のどの家もこの価格に近い可能性が高いと確信できます。

これら 2 つの地域の住宅価格の分布を視覚化する箱ひげ図を作成すると、次のようになります。

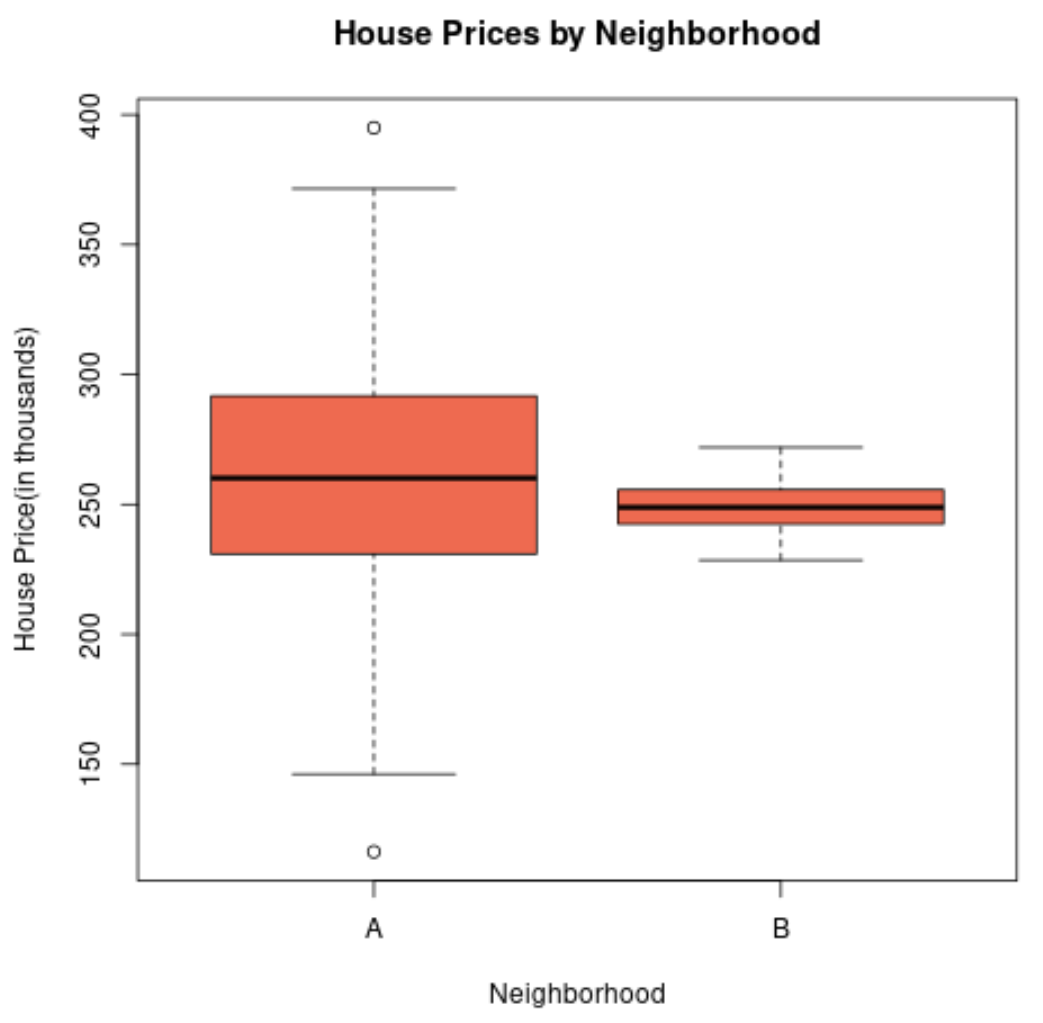
不動産価格の標準偏差がはるかに高いため、近隣 A の箱ひげ図の長さは長くなります。

実際、住宅価格は地区 A では 15 万ドル未満から 40 万ドル以上までありますが、地区 B では価格の範囲は約 23 万ドルから 27 万ドルにすぎません。

各地域の住宅価格の標準偏差を知るだけで、各地域の価格の変動がどの程度予想されるかを知ることができます。

追加リソース

適切な標準偏差とはどれくらいだと考えられますか?
範囲 vs.標準偏差: それぞれをいつ使用するか
変動係数と標準偏差: 差