標準偏差と標準誤差: 違いは何ですか?
学生が統計学でよく混同する 2 つの用語は、標準偏差と標準誤差です。
標準偏差は、データセット内の値の分布を測定します。
標準誤差は、母集団からの反復サンプルの平均の標準偏差です。
この考え方を明確に説明する例を見てみましょう。
例: 標準偏差と標準誤差
10 匹の異なるカメの体重を測定するとします。
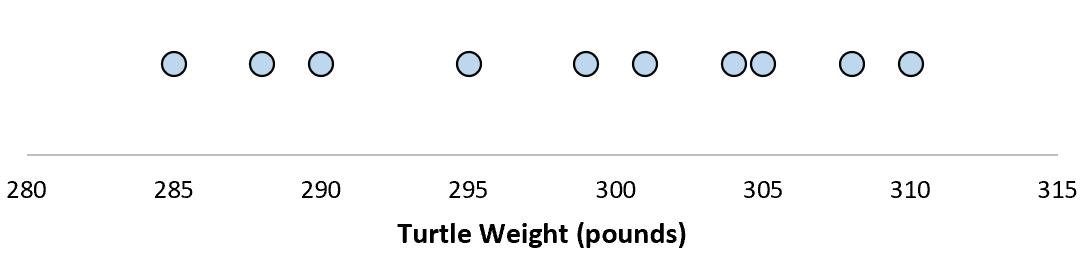
この 10 匹のカメのサンプルでは、サンプル平均とサンプル標準偏差を計算できます。
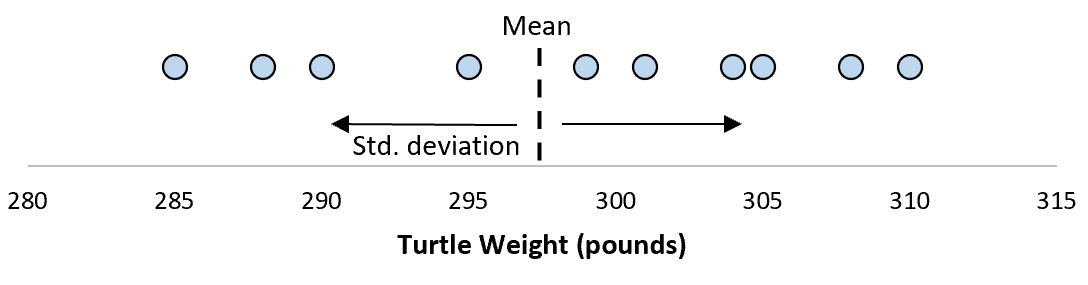
標準偏差が 8.68 であると仮定します。これにより、これらのカメの体重分布がわかります。
しかし、10 匹のカメからなる別の単純な無作為サンプルを収集し、同様に測定したとします。
この 10 匹のカメのサンプルは、同じ母集団からのものであっても、平均値と標準偏差がわずかに異なる可能性が高くなります。
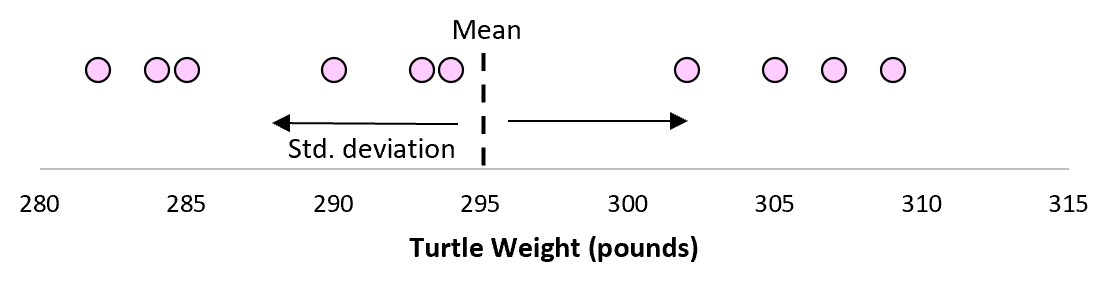
ここで、同じ母集団から繰り返しサンプルを取得し、各サンプルのサンプル平均とサンプル標準偏差を記録すると想像します。
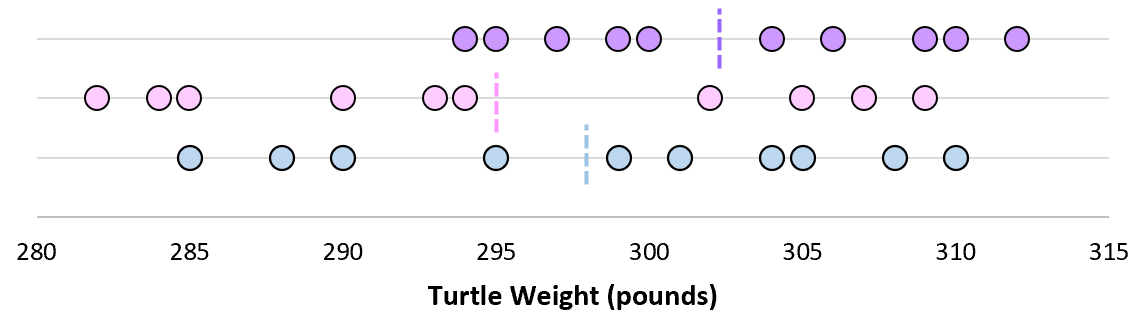
ここで、各サンプル平均を同じ線上にプロットすると想像してください。
これらの平均値の標準偏差は標準誤差と呼ばれます。
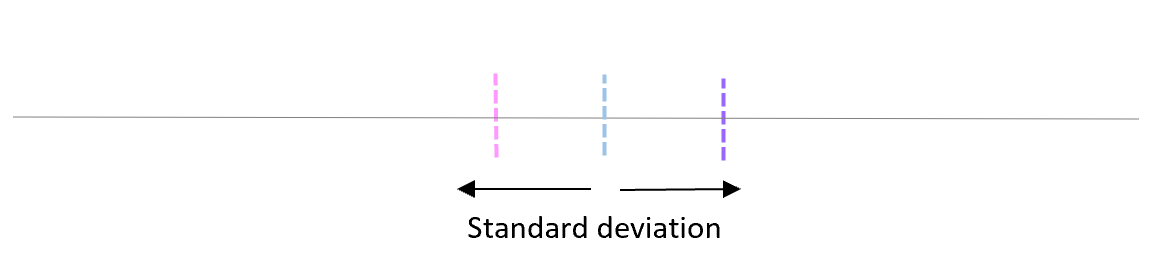
実際に標準誤差を計算する式は次のとおりです。
標準誤差 = s/√ n
金:
- s:サンプルの標準偏差
- n:サンプルサイズ
標準誤差を使用する意味は何ですか?
特定のサンプルの平均を計算するとき、実際に知りたいのはその特定のサンプルの平均ではなく、サンプルが由来するより大きな母集団の平均です。
ただし、サンプルを使用するのは、母集団全体のデータを収集するよりもサンプルのデータを収集する方がはるかに簡単であるためです。
そしてもちろん、サンプル平均はサンプルごとに異なるため、平均の推定値の精度を測定する方法として平均の標準誤差を使用します。
標準誤差の計算式では、サンプル サイズ (n) が増加するにつれて標準誤差が減少することがわかります。
標準誤差 = s/√ n
サンプルが大きくなるとばらつきが減り、サンプル平均が母集団の真の平均に近づく可能性が高まるため、これは当然のことです。
標準偏差と標準誤差をいつ使用するか
単にデータセット内の値の分布を測定したい場合は、標準偏差を使用できます。
ただし、平均の推定値に関する不確実性を定量化したい場合は、平均の標準誤差を使用できます。
特定のシナリオと達成しようとしていることに応じて、標準偏差または標準誤差の使用を選択できます。