標準偏差 (または標準偏差)

によるベンジャミン・アンダーソン博士 8月 5, 2023 統計 0コメント

この記事では、標準偏差とも呼ばれる標準偏差とは何かについて説明します。標準偏差の計算方法、段階的な実践例、および任意のデータサンプルの標準偏差を見つけるためのオンライン計算機を学びます。

標準偏差（または標準偏差）とは何ですか?

標準偏差は、標準偏差とも呼ばれ、統計的分散の尺度です。つまり、標準偏差は統計データのばらつきを示す値です。

したがって、標準偏差 (または標準偏差) は、母集団または統計サンプルの分散を定量化するために使用されます。データ系列の標準偏差が大きいほど、データはより分散しています。また、逆の解釈も可能です。標準偏差が低い場合、これは一般にデータが平均値に非常に近いことを意味します。

母集団の標準偏差または標準偏差を計算する場合、標準偏差の記号はギリシャ文字のシグマ (σ) です。ただし、標本標準偏差に関しては、統計的測定値を表すために文字 s が使用されます。

一部の統計や確率の本では、標準偏差は標準偏差とも呼ばれます。

標準偏差（または標準偏差）の式

標準偏差 (または標準偏差) は、データ系列の偏差の二乗和の平方根を観測値の総数で割ったものに等しくなります。

したがって、標準偏差 (または標準偏差) を計算する式は次のようになります。

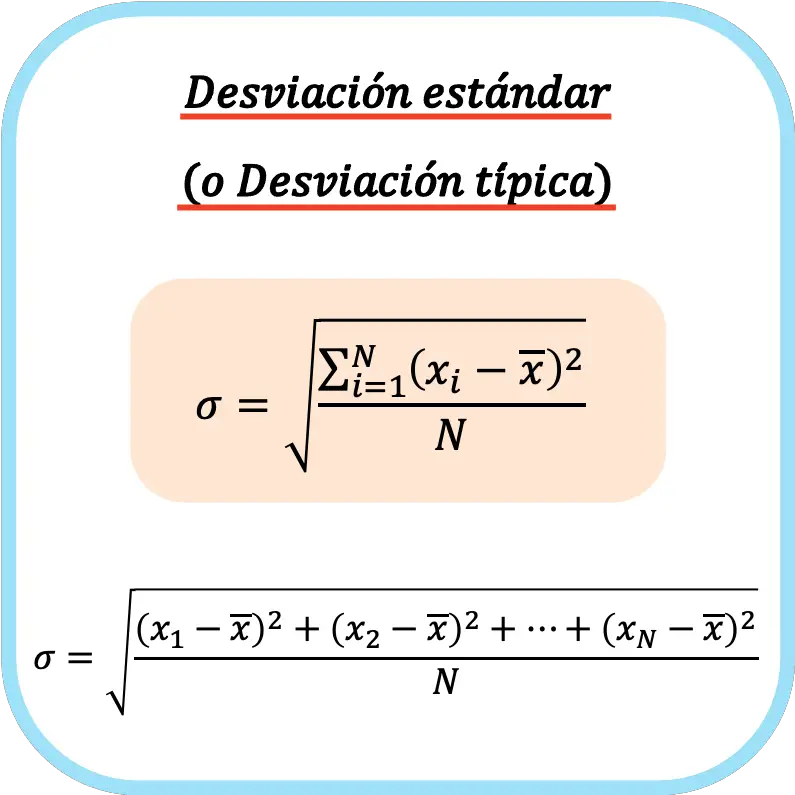
👉以下の計算機を使用して、任意のデータセットの標準偏差を計算できます。

結論として、データセットの標準偏差を見つけるには、すべての偏差 (データポイントと算術平均の差として定義) を計算し、偏差を 2 に増やし、それらをすべて加算して、次の値で割る必要があります。合計。データの数を計算し、最後に平方根を求めます。

標準偏差（または標準偏差）の例

標準偏差 (または標準偏差) の定義を考慮して、データ系列の標準偏差がどのように計算されるかを確認できるように、以下に段階的な例を示します。

次の値の標準偏差を計算します: 3、6、2、9、4。

最初に行う必要があるのは、標本の平均値を決定することです。これを行うには、すべてのデータを合計し、観測値の合計数である 5 で割ります。

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

ここでは標準偏差の公式を使用します。

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N(x_i-\overline{x})^2}{N}}$

データを式に代入します。

$\displaystyle\sigma =\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5}}$

そして最後に標準偏差を計算します。

$\begin{aligned}\displaystyle\sigma & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{5}}\\[2ex]&= \sqrt{\frac{30,8}{5}}=\sqrt{6,16}=2,48 \end{aligned}$

標準偏差 (または標準偏差) 計算ツール

一連の統計データを次のオンライン計算機に入力して、その標準偏差 (または標準偏差) を計算します。データはスペースで区切られ、小数点としてピリオドを使用して入力する必要があります。

グループ化されたデータの標準 (または典型) 偏差

間隔にグループ化されたデータの標準偏差 (または標準偏差) を計算するには、次の手順に従う必要があります。

グループ化されたデータの平均を求めます。
グループ化されたデータの偏差を計算します。
各隙間を四角にします。
以前の各結果にその間隔の頻度を掛けます。
前のステップで取得したすべての値の合計を加算します。
観測値の合計数で割ります。
前の値の平方根を計算します。結果として得られる数値は、グループ化されたデータの標準偏差です。

結論として、間隔にグループ化されたデータの標準偏差を計算する式は次のとおりです。

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}$

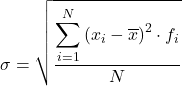
通常は上記の式を使用しますが、次のような代数式を使用しても同様の結果が得られます。

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{N}-\overline{x}^2}$

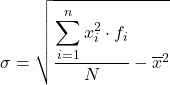
これがどのように行われるかを理解するために、以下は区間にグループ化されたデータの標準偏差に関する段階的な演習です。より正確には、次の統計データの標準偏差が計算されます。

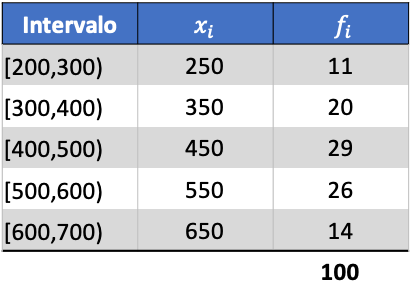
まず、算術平均を計算するために、各区間のクラススコアにその頻度を掛けます。

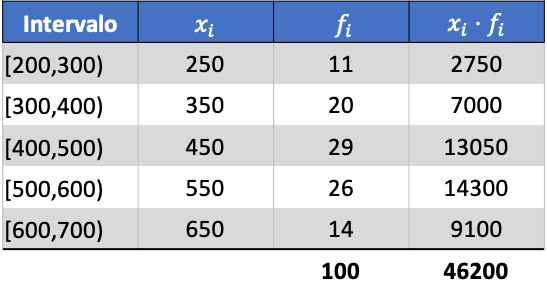
したがって、グループ化されたデータの平均は次のようになります。

$\overline{x}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{N}=\cfrac{46200}{100}=462$

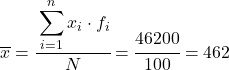
平均値がわかったので、次の 3 つの列をデータテーブルに追加する必要があります。

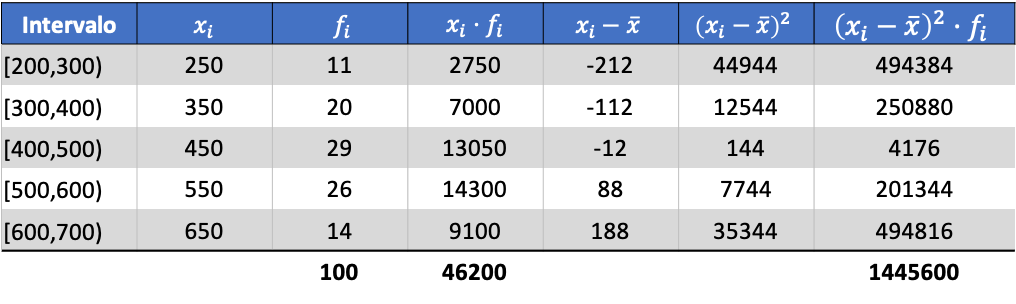
グループ化されたデータの標準偏差は、最後の列の合計の平方根を観測値の合計数で割った結果になります。

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}=\sqrt{\frac{1445600}{100}}=120,23$

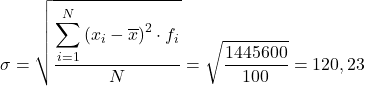
標準 (または典型) 偏差と分散

標準偏差 (または典型偏差) と分散の関係は、標準偏差が分散の平方根であるということです。

したがって、データセットの分散値がわかっていれば、平方根を取ることで標準偏差を簡単に計算できます。逆に、標準偏差がわかっている場合は、値を 2 乗することで分散を求めることができます。

$Var(X)=\sigma^2$

実際、分散は標準偏差の二乗記号を使用するだけで簡単に表すことができます。したがって、母集団分散の記号はシグマ二乗 (σ ² ) であり、標本分散の記号は s 二乗 (s ² ) です。

さらに、標準偏差と分散の概念は、どちらも一連の統計データの分散を示すため、同様の解釈を持ちます。

標準偏差（または標準偏差）の性質

標準偏差には次の特性があります。

データサンプルの標準偏差を負にすることはできません。

$\sigma \ge 0$

すべてのデータが同じであれば、標準偏差はゼロになります。

$\sigma =0$

すべてのデータに定数項を加えても標準偏差の値は変わりません。

$\sigma (X+k)=\sigma (X)$

すべてのデータに数値を乗算すると、標準偏差にはその数値の絶対値が乗算されます。

$\sigma (k\cdot X)=|k|\cdot \sigma (X)$

2 つの確率変数の合計の標準偏差は、変数の分散の合計の平方根に 2 つの変数間の共分散の 2 倍を加えたものに等しくなります。

$\sigma(X+Y)=\sqrt{Var(X)+Var(Y)+2\cdot Cov(X,Y)}$

さまざまな分布の標準偏差 (σ _i ) とそのデータ数 (n _i ) がわかっている場合は、次の式を適用して合計標準偏差を計算できます。

$\displaystyle\sigma=\sqrt{\frac{\displaystyle \sum_{i=1}^N n_i\cdot \sigma_i^2}{\displaystyle \sum_{i=1}^N n_i}}=\sqrt{\frac{\displaystyle n_1\cdot \sigma_1^2+n_2\cdot \sigma_2^2+\dots +n_N\cdot \sigma_N^2}{\displaystyle n_1+n_2+\dots+n_N}}$

著者について

ベンジャミン・アンダーソン博士

私はベンジャミンです。退職した統計教授から、専任の Statorials 教育者になりました。統計分野における豊富な経験と専門知識を活かして、私は Statorials を通じて学生に力を与えるために自分の知識を共有することに尽力しています。もっと知る