正規分布と t 分布: 違いは何ですか?

正規分布は、すべての統計で最も一般的に使用される分布であり、対称で釣鐘型であることが知られています。

密接に関連した分布はt 分布です。これも対称で釣鐘型ですが、正規分布よりも重い「尾部」を持っています。

言い換えると、正規分布と比較すると、分布内の値が中心よりも端に多く配置されます。

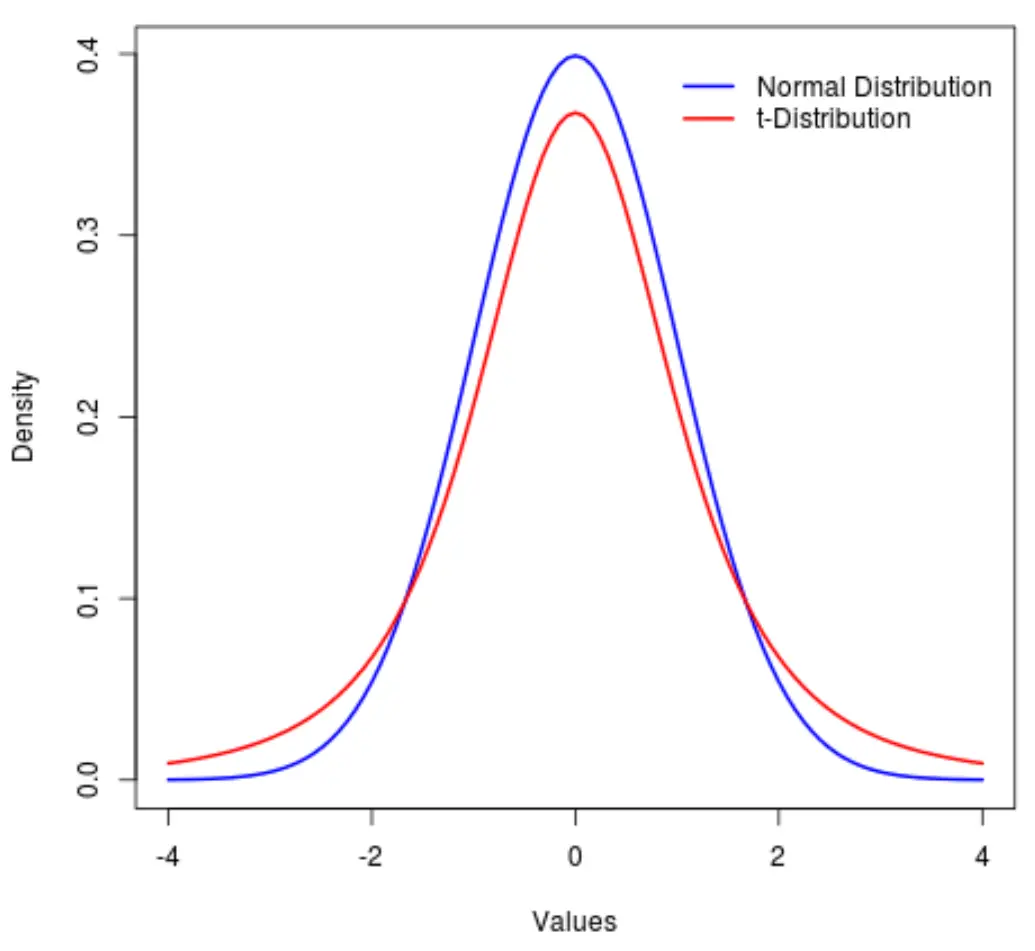
統計用語では、分布がどの程度「重い」かを測定するために尖度と呼ばれる指標を使用します。したがって、 t 分布の尖度は正規分布の尖度よりも大きいと言えます。

実際には、仮説検定を実行したり信頼区間を構築したりするときに、t 分布を使用することが最もよくあります。

たとえば、母集団平均の信頼区間を計算する式は次のとおりです。

信頼区間 = x +/- t _{1-α/2, n-1} *(s/√ n )

金：

• x :サンプルの平均値
• t:有意水準αとサンプル サイズnに基づく臨界 t 値
• s:サンプルの標準偏差
• n:サンプルサイズ

この式では、次の条件のいずれかが当てはまる場合、テーブル z の臨界値の代わりにテーブル t の臨界値を使用します。

• 母集団の標準偏差はわかりません。
• サンプルサイズは 30 以下です。

次のフローチャートは、テーブル t とテーブル z のどちらの重要な値を使用する必要があるかを知る便利な方法を示しています。

信頼区間を構築する際に t 分布を使用する場合と正規分布を使用する場合の主な違いは、t 分布の臨界値が大きくなり、信頼区間が広くなる点です。

たとえば、次の情報を含むランダムなカメのサンプルを収集するために、カメの集団の平均体重の 95% 信頼区間を構築するとします。

• サンプルサイズn = 25
• 平均サンプル重量x = 300
• サンプル標準偏差s = 18.5

95% 信頼水準の臨界 z 値は1.96ですが、自由度 df = 25-1 = 24 の 95% 信頼区間の臨界 t 値は2.0639です。

したがって、Z 臨界値を使用した母平均の 95% 信頼区間は次のようになります。

95% CI = 300 +/- 1.96*(18.5/√ 25 ) = [292.75, 307.25]

一方、t 臨界値を使用した母平均の 95% 信頼区間は次のようになります。

95% CI = 300 +/- 2.0639*(18.5/√25) = [292.36, 307.64]

t-critical 値の信頼区間が広いことに注意してください。

ここでの考え方は、サンプルサイズが小さい場合、母集団の真の平均値に対する確信度が低くなるため、t 分布を使用して、母集団の真の平均値が含まれる可能性が高くなる広い信頼区間を生成すると便利であるということです。

t 分布の自由度の視覚化

自由度が増加するにつれて、t 分布は正規分布に近づくことに注意してください。

これを説明するために、次の自由度を持つ t 分布の形状を示す次のグラフを考えてみましょう。

• df = 3
• df = 10
• df = 30

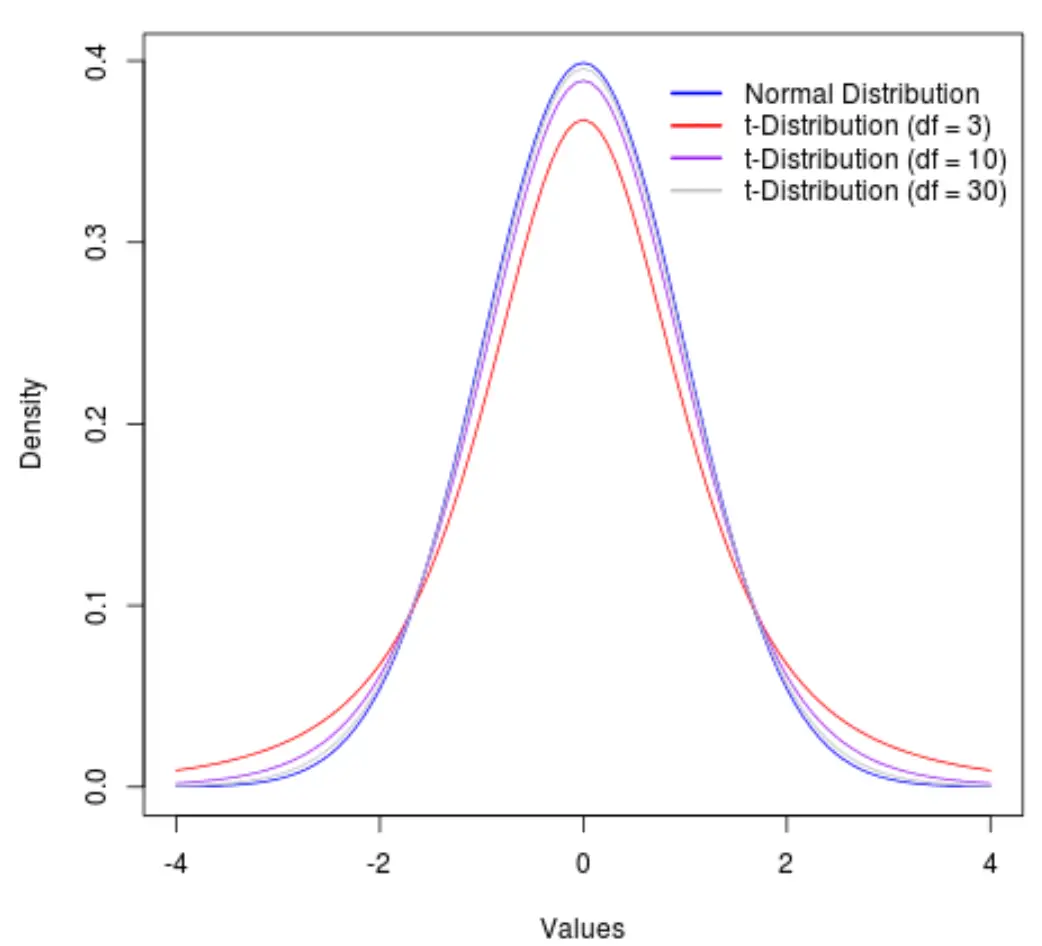
自由度が 30 を超えると、t 分布と正規分布は非常に類似するため、式で t 臨界値を使用する場合と z 臨界値を使用する場合の違いは無視できるほどになります。