残差標準誤差の解釈方法
残差標準誤差は、回帰モデルがデータセットにどの程度適合するかを測定するために使用されます。
簡単に言えば、回帰モデルの残差の標準偏差を測定します。
次のように計算されます。
残差標準誤差 = √ Σ(y – ŷ) 2 /df
金:
- y:観測値
- ŷ:予測値
- df:自由度。観測値の合計数 – モデル パラメーターの合計数として計算されます。
残差標準誤差が小さいほど、回帰モデルはデータセットに適合します。逆に、残差標準誤差が高くなるほど、回帰モデルはデータセットに適合しにくくなります。
残差標準誤差が小さい回帰モデルでは、近似された回帰直線の周囲にデータ ポイントが密集して存在します。
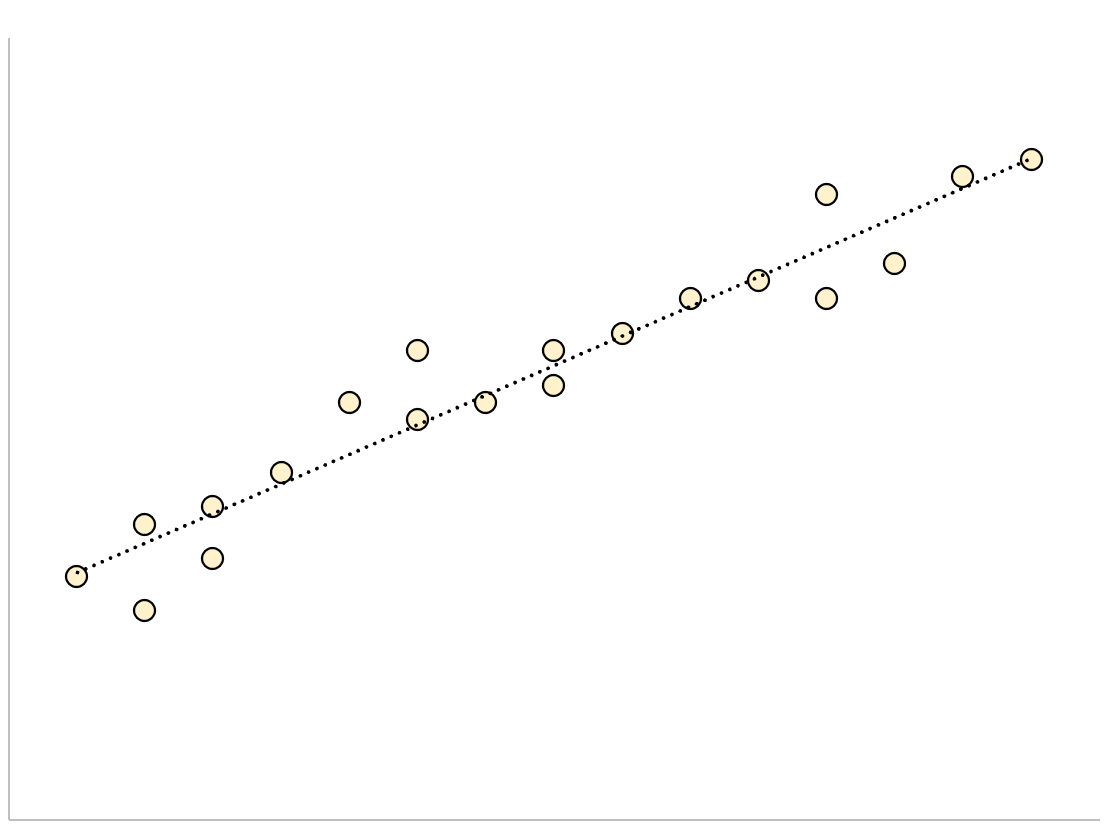
このモデルの残差(観測値と予測値の差) は小さくなります。つまり、残差標準誤差も小さくなります。
逆に、残差標準誤差が大きい回帰モデルでは、データ ポイントが近似された回帰直線の周囲にさらに緩やかに分散されます。
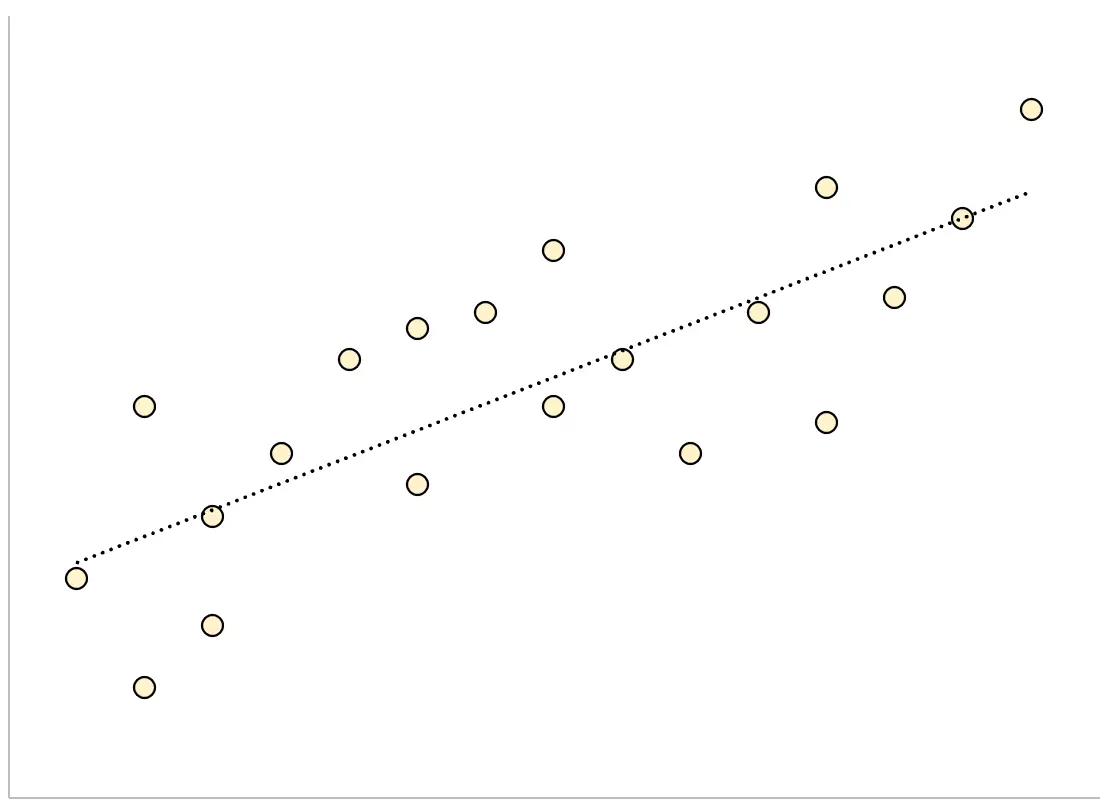
このモデルからの残差は大きくなり、これは残差の標準誤差も大きくなることを意味します。
次の例は、R で回帰モデルの残差標準誤差を計算して解釈する方法を示しています。
例: 残差標準誤差の解釈
次の重線形回帰モデルを近似したいとします。
mpg = β 0 + β 1 (変位) + β 2 (動力)
このモデルは、予測変数「排気量」と「馬力」を使用して、特定の車が走行するガロンあたりの走行マイル数を予測します。
次のコードは、この回帰モデルを R に適合させる方法を示しています。
#load built-in mtcars dataset data(mtcars) #fit regression model model <- lm(mpg~disp+hp, data=mtcars) #view model summary summary(model) Call: lm(formula = mpg ~ disp + hp, data = mtcars) Residuals: Min 1Q Median 3Q Max -4.7945 -2.3036 -0.8246 1.8582 6.9363 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 30.735904 1.331566 23.083 < 2nd-16 *** available -0.030346 0.007405 -4.098 0.000306 *** hp -0.024840 0.013385 -1.856 0.073679 . --- Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 3.127 on 29 degrees of freedom Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09
結果の下部に向かって、このモデルの残差標準誤差が3.127であることがわかります。
これは、回帰モデルが自動車の mpg を平均誤差約 3,127 で予測していることを示しています。
残差標準誤差を使用してモデルを比較する
残差標準誤差は、さまざまな回帰モデルの適合を比較する場合に特に役立ちます。
たとえば、2 つの異なる回帰モデルを当てはめて自動車の燃費を予測するとします。各モデルの残差標準誤差は次のとおりです。
- モデル 1 の残留標準誤差: 3.127
- モデル 2 の残留標準誤差: 5.657
モデル 1 は残差標準誤差が低いため、モデル 2 よりもデータによく適合します。 したがって、モデル 1 を使用して自動車の走行速度を予測することを好みます。これは、モデル 1 で行われる予測が、観測された自動車の走行速度の値に近いためです。