割合の信頼区間
この記事では、割合の信頼区間とは何か、またそれが統計で何に使用されるのかについて説明します。同様に、比率の信頼区間を計算する方法と、概念をよりよく理解するための解決済み演習を学習します。
比率の信頼区間はどれくらいですか?
割合の信頼区間は、母集団の割合の許容値の範囲を提供する区間です。つまり、割合の信頼区間は、母集団の割合が誤差の範囲内にある最大値と最小値を示します。
たとえば、信頼水準が 95% である母集団の割合の信頼区間が (0.73, 0.81) である場合、これは、母集団の割合が 73% ~ 81% の間にあり、確率が 95% であることを意味します。
したがって、割合の信頼区間は、特定の特性を満たす母集団の割合の値を推定するために使用されます。
次のセクションで説明するように、割合の信頼区間はサンプルの割合とサンプル内の観測値の数に依存します。
比率の信頼区間の式
比率の信頼区間は、Z α/2の値にサンプル比率 (p) の平方根を掛け、1-p を掛けてサンプル サイズ (n) で割った値をサンプル比率に加算および減算することによって計算されます。したがって、比率の信頼区間を計算する式は次のとおりです。

金:
-

はサンプルの割合です。
-

はサンプルサイズです。
-

α/2 の確率に対応する標準正規分布の分位数です。サンプルサイズが大きく、95% の信頼水準の場合は通常 1.96 に近く、99% の信頼水準の場合は通常 2.576 に近くなります。
割合の信頼区間の計算例
割合の信頼区間がどのように計算されるかを理解できるように、以下に具体的な例をステップごとに示します。
- 保険会社は市場調査を実施し、国内で生命保険に加入している人が何人いるかを調べたいと考えています。これを行うために、700 人の無作為サンプルが分析され、サンプルの 40% が生命保険に加入しているという結論に達しました。国の人口に占める割合の 95% 信頼水準の信頼区間はどれくらいですか?
母集団の割合の信頼区間を決定するには、上で見た式を使用する必要があります。

この場合、信頼区間の信頼水準を 95% にする必要があるため、取得する必要がある Z α/2の値は 1.96 です。
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-54dda39d0da5b29f2d25728b89565859_l3.png)
問題ステートメントでは、サンプル サイズが n=700 で、サンプル内で観察された割合が p=0.40 であることがすでに示されているため、割合の信頼区間の式にデータを代入し、区間の限界を計算します。

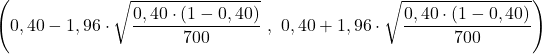
![]()
結論として、調査対象の母集団の割合は 36% ~ 44% であり、信頼水準は 95% です。