決定係数(r2乗)
この記事では、統計における決定係数 (または R 二乗) とは何かについて説明します。したがって、決定係数の計算方法、その解釈方法、さらにはデータ サンプルの決定係数を計算するためのオンライン計算機もわかります。
決定係数 (R の 2 乗) は何ですか?
決定係数(記号はR 2 ( R 二乗) ) は、回帰モデルの適合度を測定する統計量です。決定係数は、回帰モデルがデータセットにどの程度適合しているかを示します。つまり、回帰モデルによって説明される割合を示します。
したがって、決定係数が高いほど、回帰モデルは優れています。この条件は常に満たされるわけではありませんが、原則としてできるだけ大きな決定係数に関心があります。決定係数をどのように解釈するかを以下で見てみましょう。
係数の決定式
決定係数は、1 から残差分散と従属変数の分散の間の比を引いたものに等しくなります。決定係数は、平方和の総和に対する残差から 1 から平方和を引いた値を引くことによっても計算できます。
したがって、決定係数の計算式は次のようになります。

金:
-

は決定係数です。
-
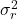
は残差分散です。
-

従属変数 Y の分散です。
-
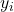
観測従属変数 i の値です。
-
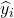
は、観測値 i の回帰モデルによって近似された値です。
-

すべての観測値にわたる従属変数の平均です。
👉以下の計算機を使用して、任意のデータセットの決定係数を計算できます。
線形回帰モデルの場合、決定係数は相関係数の 2 乗に相当します。
![]()
金
![]()
は変数 X と Y の共分散です。
![]()
そして
![]()
は、それぞれ独立変数 X と従属変数 Yの分散です。
決定係数計算機
サンプル データを以下の計算機に接続して、単純な線形回帰モデルを当てはめ、その決定係数を計算します。最初のボックスには独立変数 X の値のみが含まれ、2 番目のボックスには従属変数 Y の値のみが含まれるように、データのペアを分離する必要があります。
データはスペースで区切られ、小数点としてピリオドを使用して入力する必要があります。
決定係数の解釈
このセクションでは、決定係数を解釈する方法を見ていきます。決定係数の値を知っていても、後でそれが何を意味するのかが分からなければ意味がありません。
決定係数の値の範囲は 0 ~ 1 ですが、通常はパーセンテージで表されるため、最小値は 0%、最大値は 100% になります。
決定係数の解釈に関しては、その値が高いほど、回帰モデルがデータ サンプルをよりよく説明していることを意味します。したがって、決定係数が 1 に近づくほど、モデルはより多く調整されます。一方、0 に近づくほど、作成される回帰モデルの信頼性は低くなります。
ただし、2 つの回帰モデルを比較する場合、回帰係数が高いモデルの方が必ずしも優れているとは限りません。たとえば、回帰モデルは回帰係数 R 2 = 100% を持つ場合があります。これは、多くの説明変数がモデルに追加されており、すべての観測値を完全に説明できるためです。しかし、このモデルは、回帰モデルの構築に使用されなかった新しい値に対して非常に悪い予測を行うことは確かです。
また、結果として得られる回帰モデルが以前の仮定を満たしていることにも留意する必要があります。したがって、決定係数が非常に高いモデルは、残差の変動が一定でない場合 (等分散性) は役に立ちません。
さらに、決定係数は説明変数を含めることに不利益を与えるものではないため、重要な制限を提示します。論理的には、回帰モデルに含まれる説明変数が多いほどモデルは複雑になりますが、観察されたデータをより適切に説明できるため、決定係数は高くなります。ただし、調整された決定係数には、モデル内の変数の数が考慮されます (計算方法は以下で説明します)。
結論として、決定係数は回帰モデルがデータセットにどの程度適合しているかを知ることができるため、回帰モデルの分析に非常に役立ちます。ただし、結果のモデルをレビューするには、統計グラフなどの他のツールも使用する必要があります。
調整後の決定係数
調整された決定係数 は、調整された決定係数とも呼ばれ、モデルに含まれる説明変数の数を考慮して、回帰モデルの適合度を測定します。
決定係数と調整された決定係数の違いは、決定係数は変数の数を考慮せずに調整の質を測定するのに対し、調整された決定係数は調整の質を測定することです。追加された変数ごとにペナルティを課します。
調整後の決定係数の計算式は次のとおりです。
![]()
金:
-

は調整された決定係数です。
-

は決定係数です。
-

はサンプルサイズです。
-

回帰モデル内の説明変数の数です。
したがって、モデルの説明変数の数が異なる可能性があるため、調整された決定係数は 2 つの異なるモデルを比較する場合の決定係数よりも優れています。